高三级数学科第四次月考试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题:本题共有12个小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一个是正确的.请将正确结论的代号填入答题卷选择题的答题卡表格中.
1.已知全集U={1,2,3,4,5,6,7,8},A={3,4,5},B={1,3,6},那么集合M={2,7,8}是
(A) A∪B (B) A∩B (C) CUA∪CUB (D) CUA∩CUB
2.等比数列{an}中,Tn表示该数列的前n项的积,若T5=1,则
(A) a1=1 (B) a3=1 (C) a4=1 (D) a5=1
3.复数![]() 的值是
的值是
(A) i (B) -i (C) 1 (D) -1
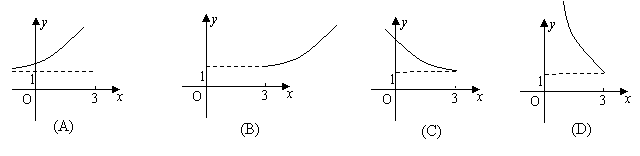
4.下列四个图形中,与函数y=3+log2x(x≥1)的图象关于直线y=x对称的图形是
5.函数f (x)=(sinx+cosx)2+2cos2x的最大值是
(A) 2 (B) 3 (C) 2+ (D) 4
6.若![]() ,则a、b值分别是
,则a、b值分别是
(A) a=14,b=-51 (B) a=-14,b=51 (C) a=14,b=51 (D) a=-14,b=-51
7.函数f (x)=x+2cosx在闭区间[0, ]上的最大值是
(A) 2 (B) 1+ (C) (D) +
8.关于x的不等式![]() 的解集为R的充要条件是
的解集为R的充要条件是
(A) m<0 (B) m≤-1 (C) m≤0 (D) m≤1
9.等差数列{an}的前n项和为Sn,且a1>0,若存在自然数m≥3,使得am=Sm,则当n>m时,Sn与an的大小关系为
(A) Sn>an (B) Sn≥an (C) Sn<an (D) Sn≤a
10.已知tan110°= a,求tan50°的值(用a表示),甲得到的结果是![]() ,乙得到的结果是
,乙得到的结果是![]() ,对此你的判断是
,对此你的判断是
(A) 甲对乙错 (B) 乙对甲错 (C) 甲、乙都对 (D) 甲、乙都错
11.若函数y=![]() + 在区间(0,1)上是减函数,则实数a的取值范围是
+ 在区间(0,1)上是减函数,则实数a的取值范围是
(A) [1, +∞) (B) (1,+∞) (C) (-∞,1] (-∞,1)
12.假设世界人口自1980年起,50年内每年增长率均固定,已知1987年世界人口达50亿,1999年第60亿个人诞生在赛拉佛耶.根据这些资料推测2023年世界人口数最接近下列哪一个数
(A) 92亿 (B) 86亿 (C) 80亿 (D) 75亿
第Ⅱ卷(非选择题 共90分)
二、填空题:本题共有4小题.只要求直接填写结果,每题填对得4分,否则一律是零分.本题满分16分.
13.曲线![]() 处切线的倾斜角为
处切线的倾斜角为
14.设数列![]() ,其中数列
,其中数列![]() 是公差为2的等差数列且
是公差为2的等差数列且![]() 则
则![]() 的值为
.
的值为
.
15.若f (x)是R上的减函数,且f (x)的图象经过点A (0,3)和B (3,-1),则不等式 f (x+1)-1<2的解集是
16.已知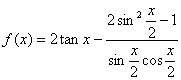 ,则
,则![]() =
=
高三级数学科第四次月考答题卷
| 题号 | 一 | 二 | 三 | 总分 | ||||||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||||||
| 得分 | ||||||||||||
一、第Ⅰ卷选择题答题处:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、第Ⅱ卷填空题答题处:
13. ;14. ;
15. ;16. .
三、解答题:本题共有6小题,要求写出解答过程和演算、证明步骤.本题满分74分.
17.(本小题满分12分)
已知![]() 的值.
的值.
18.(本小题满分12分)
已知关于x的不等式![]() 的解集为M.
的解集为M.
(Ⅰ)当a=4时,求集合M;
(Ⅱ)若3∈M且5![]() M,求实数a的取值范围.
M,求实数a的取值范围.
19.(本小题满分12分)
设函数f (x)=(1+x)2-ln(1+x)2.
(1)求f (x)的单调区间;
(2)若当![]() 时,不等式f (x)<m恒成立,求实数m的取值范围;
时,不等式f (x)<m恒成立,求实数m的取值范围;
20.(本小题满分12分)
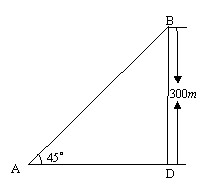
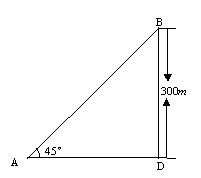
如图,某海滨浴场的岸边可近似地看作直线a,救生员现在岸边的A处,发现海中的B处有人求救,救生员没有直接从A处游向B处,而是沿岸边A跑到离B最近的D处,然后游向B处,若救生员在岸边的行进速度为6米/秒,在海水中的行进速度为2米/秒。
(1)分析救生员的选择是否正确;
(2)在AD上找一处C,使救生员从A到C再到B的时间为最短,并求出最短时间.
21.(本小题满分12分)
已知数列{an}的各项均为正整数,且满足![]() 又
又![]() .
.
(Ⅰ) 求a1,a2,a3,a4的值,并由此推测出{ an}的通项公式(不要求证明);
(Ⅱ) 设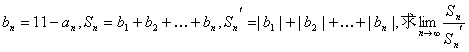 的值;
的值;
(Ⅲ) 设![]() 是否存在最大的整数m,使得对任意n∈N,均有
是否存在最大的整数m,使得对任意n∈N,均有![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
22.(本小题满分14分)
已知函数![]() 的定义域为R,且
的定义域为R,且![]()
(1)求证:![]()
(2)若![]() 求证:
求证:![]()
高三级数学科第四次月考参考答案与评分标准
一、第Ⅰ卷选择题答题处:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | B | B | C | A | D | A | C | C | A | B |
二、第Ⅱ卷填空题答题处:
13. 135° ;14. 1 ;15. (-1,2) ;16. 8 .
三、解答题:本题共有6小题,要求写出解答过程和演算、证明步骤.本题满分74分.
17.解:![]() ………………………………5分
………………………………5分
由![]() 两边平方得
两边平方得![]()
![]() ……………………………9分
……………………………9分
而![]() ,故原式
,故原式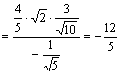 ………………………………12分
………………………………12分
18.解:(Ⅰ)当a =
4时,原不等式可以化为![]() ………………2分,即
………………2分,即![]() ………………4分
………………4分
![]() 故 M为
故 M为![]() …………………………………6分
…………………………………6分
(Ⅱ)由3∈M得:![]() ①…8分,且5
①…8分,且5![]() ②…10分
由①②得:
②…10分
由①②得:![]() …12分
…12分
19.解:(1)![]() ,………………………… 2分
,………………………… 2分
由![]() >0得-2<x<-1或x>0,∴f (x)的单调递增区间为(-2,-1)和(0,+∞)………………………… 4分
>0得-2<x<-1或x>0,∴f (x)的单调递增区间为(-2,-1)和(0,+∞)………………………… 4分
由![]() <0得x<-2或-1<x<0,∴f (x)的单调递减区间(-∞,-2)和(-1,0)
…………………………6分
<0得x<-2或-1<x<0,∴f (x)的单调递减区间(-∞,-2)和(-1,0)
…………………………6分
(2)当![]() 时,令
时,令![]() =0得x=0,(8分)∵函数f (x)在闭区间
=0得x=0,(8分)∵函数f (x)在闭区间![]() 上连续,
上连续,
且f (0=1,![]() e-2+2,f (e-1)=e2-2,∵e2-2> e-2+2>1,∴fmax (x)=f (e-1)=e2-2,………………………… 10分
e-2+2,f (e-1)=e2-2,∵e2-2> e-2+2>1,∴fmax (x)=f (e-1)=e2-2,………………………… 10分
故不等式f (x)<m恒成立等价于m> fmax (x),即m>e2-2. …………………………12分
 20.解:(1)A到B的时间t1=150
20.解:(1)A到B的时间t1=150![]() 秒,A到D再由D到B的时间
秒,A到D再由D到B的时间![]() …………………………2分
…………………………2分
![]() 救生员的选择是正确的……………………4分
救生员的选择是正确的……………………4分
(2)设![]() 从A到C再到B的时间
从A到C再到B的时间
![]() …………………6分
…………………6分
![]() …………………………8分,当且仅当
…………………………8分,当且仅当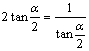
![]() ………………………10分
………………………10分![]() …………12分
…………12分
21.解:(Ⅰ)由![]() 解得
解得![]() (舍).…………1分
(舍).…………1分
由![]() (舍)……2分 同理可求出
(舍)……2分 同理可求出![]() .…3分
.…3分
由此推测an的通项公式:![]() .…………4分
.…………4分
(Ⅱ)![]() 可知数列
可知数列![]() 是等差数列.
是等差数列.![]() ……5分
……5分
当![]() 当
当![]() ……6分
……6分
当![]() .
. ![]() ……8分
……8分
(Ⅲ)![]() …………………………9分
…………………………9分
![]() ……10分
……10分
对于任意![]() .
. ![]()
![]() 是关于n的递增函数.…………11分∴要使
是关于n的递增函数.…………11分∴要使![]() 对任意
对任意![]() 总成立,只要
总成立,只要![]() .即
.即![]() .
. ![]() .因此存在整数m,使得对任意
.因此存在整数m,使得对任意![]() ,均有
,均有![]() ,且m的最大值为7.…………12分
,且m的最大值为7.…………12分
22.解:(1)![]() …………………………2分
…………………………2分
若![]()
![]()
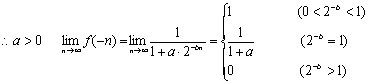 …………………………5分
…………………………5分
![]() …………………………7分
…………………………7分
(2)由(1)![]()
![]() …………………………9分
…………………………9分
![]() …………………………11分
…………………………11分
![]() …………………………12分
…………………………12分
![]() )
)
![]() …………………………14分
…………………………14分