高三联合考试数学试卷
一、填空题（本大题共48分，每小题4分）
1．若复数
的实部与虚部相等，则实数
的值为__________。
2．已知函数
，则
__________。
3．若方程
的一个根为
，则
__________。
4．若
展开式中
的系数为
，则常数
__________。
5．从抛物线
图象上一点
引抛物线准线的垂线，垂足为
，且
，设抛物线焦
点为
，则
的面积为__________。
6．已知
，
，若
，则实数
的取值范围是________。
7．若
，则
的一个表达式为_________________（只需写出一个）。
8．（理）已知极坐标系中，
，
两点，那么直线
与极轴所在直线所夹的锐
角是__________。
（文）已知
，则
的最大值是__________。
9．某四所大学进行自主招生，同时向一所高中的已获市级竞赛一等奖的甲、乙、丙、丁四位学
生发出录取通知书。若这四名学生都愿意进这四所大学的任意一所就读，则仅有两名学生录
取到同一所大学的概率为____________。
10．定义一种运算“*”，对于
，满足以下运算性质：
① 
；② 
。则
的数值为__________。
11．上海市人口和计划生育委员会发布的人口出生预测数据为
 |
年份 2003年 2004年 2005年 2006年
 |
常住人口出生数 
万
万 
万 
万
 |
根据表中信息，按近4年的平均增长率的速度增长，从________年开始，常住人口出生数超过2003年出生数的2倍。
12．已知命题：平面上一矩形
的对角线
与边
和
所成角分别为
，则
。若把它推广到空
间长方体中，试写出相应的命题形式：____________________
_____________________________________________________。
二、选择题（本大题共16分，每小题4分）
13．若
是异面直线，则以下命题正确的是
（ ）
（A）至多有一条直线与都垂直
（B）至多有一个平面分别与平行
（C）一定存在平面与所成角相等 （D）一定存在平面同时垂直于
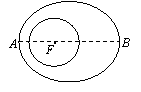14．我国发射的神舟5号飞船开始运行的轨道是以地球的中心为一个
焦点的椭圆，测得近地点
距地面200公里，远地点
距地面350
公里，地球的半径为6371公里，则从椭圆轨道上一点看地球的最大
视角为 （ ）
（A）
（B）
（C）
（D）
15．在
中，角
的对边分别是
，且
，则
等于 （ ）
（A）
（B）
（C）
（D）
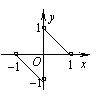16．如图，
的定义域为
，则不等式
的解集为（ ）
（A）
（B）
（C）
（D）
三、解答题（本大题共86分）
17．（本题满分12分）
（1）已知
且
，求
的值；
（2）记
（
），求的最大值及对应的值。
18．（本题满分12分）如图，在正方体
中，
是棱
的中点，
为平面
内一点，
。
（1）证明
平面；
（2）求
与平面所成的角；
（3）若正方体的棱长为，求三棱锥
的体积。
19．（本题满分14分）本市某区大力开展民心工程，近几年来对全区
的老房子进行平改坡。
且每年平改坡面积的百分比相等，若改造到面积的一半时，所用时间需10年。已知到今年为
止，平改坡剩余面积为原来的
。
（1）问到今年为止，该平改坡工程已进行了多少年？
（2）若通过技术创新，至少保留
的老房子开辟新的改造途径。今后最多还需平改坡多少年？
20．（本题满分14分）
（1）已知平面上两定点、的距离为4，点满足
，求点的轨迹方程；
（2）若把(1)的的轨迹图象向右平移一个单位，再向下平移一个单位，恰与直线
相切，试求实数
的值；
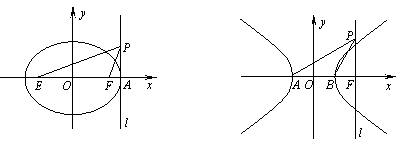
（3）如图，
是经过椭圆
长轴顶点且与长轴垂直的直线，
是两个
焦点，点
，不与重合。若
，则有
，类比此结论到双曲线
，是经过焦点且与实轴垂直的直线，
是两个顶点，点
，不与重合。若
，试求角的取值范围。
 |
21．（本题满分16分）已知函数
，
。
（1）试求函数
的反函数
；
（2）函数
，求
的定义域，并判断函数的增减性；
（3）（理）若（2）中函数，有
在定义域内恒成立，求的范围。
（文）若（2）中函数的最小值为3，试求的值。
22．（本题满分18分）
（1）已知数列
的通项公式：
，试求最大项的值；
（2）记
，且满足（1），若
成等比数列，求
的值；
（3）（理）如果
，且是满足（2）的正常数，试证：对于任意
自然数
，或者都满足
；或者都满足
。
（文）若
是满足（2）的数列，且成等比数列，
试求满足不等式：
的自然数的最小值。
高三联合考试数学试卷 参考答案
一、填空题 1．2 2．
3．
4．2 5．10 6．
7．
8．(理)
(文)2 9．
10．3004 11．2010 12．长方体
中，对角线
与棱
所成的角分别为
，则
，
。或是：长方体中，对角线与平面
所成的角分别为，则
，
。或是：长方体中，对角面
与平面
所成的二面角分别为
，则
。
二、选择题 13．C 14．B 15．A 16．D
三、解答题
17．（1）
，
，又
，∴
或
。
（2）
，当
，即
时，
。
18．（1）设正方体的棱长为
，则
，
，
∵
，∴
，又
，∴
平面
。
（2）
，设
与
所成的角为
，
，∴
。
由（1）知平面，∴
为
与平面所成的角。
。
（3）
。
19．设每年平改坡的百分比为
，则
。
（1）设到今年为止，该工程已经进行了
年，则
。
故到今年为止，该工程已经进行了5年。
（2）设今后最多还需平改坡
年，则
。
故今后最多还需平改坡15年。
20．（1）以
中点
为原点，所在直线为轴，建立平面直角坐标系，则
。
设
，由
得
，此即点的轨迹方程.
（2）将向右平移一个单位，再向下平移一个单位后，得到圆
，
依题意有
。
（3）不妨设点
在
的上方，并设
，则
，
所以
，由于
且
，故
。
21．（1）易求
。
（2）
，
时，定义域为
；
时，定义域为
；
此函数在定义域内单调递增（∵
与
在公共定义域内均为增函数，∴它们的和也为增函数）。
（3）（理）当时，由
。
当时，由
。∴的取值范围是
。
（文）当时，由
；
当时，由
。 ∴所求的的值为
或
。
22．（1）
，∴
，则
。即
的最大项的值为4。
（2）欲使
成等比数列，只需
成等比数列。
∵
，∴只需
或
即可。解得
或
。
（3）（理），
，∵
，∴
。又
，∴
。
∵
，∴
；或
。
（文）∵不合题意，∴
，据题意，
，
。