高三年级调研考试数学试卷
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页．共150分．考试时间120分钟．
第 I 卷 （选择题 共60分）
注意事项：
1．答第I卷前，考生务必将自己的姓名、考生号、考试科目用铅笔涂写在答题卡上．
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．
3．考试结束，监考人员将本试卷和答题卡一并收回．
参考公式：
 |
一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
（1）a、b为非零实数，
，则A中元素个数是
（A）1 （B）2 （C）3 （D）4
（2）（文科做）若实数
的值是
（A）
（B）
（C）
（D）
（文科做）若复数
（i为虚数单位，b为实部）的实部和虚部互为相反数，则b等于
（A）
（B）
（C）
（D）2
（3）函数
的值域为
，则
的值域是
（A）
（B）
（C）
（D）
（4）x为三角形的一个内角，且
，则
等于
（A）
（B）
（C）或
（D）
（5）若
，则k的值是
（A）
（B）6
（C）3 （D）
（6）m，n是互不垂直的直线，平面
则下列关系中不可能成立的是
（A）
（B）
（C）
（D）
（7）点P在曲线
上移动，设点P处切线的倾斜角为
，则的取值范围是
（A）
（B）
（C）
（D）
（8）已知数列
的值为
（A） （B）
（C）或 （D）
（9）设椭圆
的离心率分
别为
，则
（A）
（B）
（C）
（D）
大小不确定
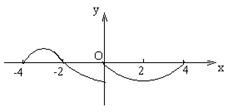
（10）偶函数
，奇函数
的定义域均为
；
在
，
在
上的图
象如图，则不等式
的解集为
（A）
（B）
（C）
（D）
（11）在数列
中
（文科做）则k等于
（A）
（B）1
（C）0
（D）2
（理科做）则
等于
（A）
（B）3
（C）0
（D）1
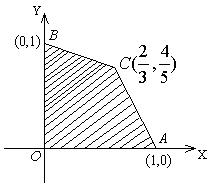（12）如图，目标函数
的可行域为四边形OACB (含边界)，若
是该目标函数的最优
解，则a的取值范围是
（A）
（B）
（C）
（D）
高三年级调研考试
数 学 试 卷 2004年3月
第 Ⅱ 卷 （选择题 共90分）
注意事项：
⒈ 第Ⅱ卷共4页，用钢笔或圆珠笔直接答在试题卷中．
⒉ 答卷前将密封线内的项目填写清楚．
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 分数 | |||||||||
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上。
（13）若
展开式中只有第4项系数最大，那么它的常数项为____________．
（14）某校有高中生1200人，初中生900人，老师120人，现用分层抽样的方法从所有师生中抽取
一个容量为N的样本；已知从初中生中抽取人数为60人，那么N =___________．
（15）5名同学参加某竞赛，排出第一名至第五名，老师告诉甲、乙两同学，对甲说：“你和乙都没
有拿到第一名”，对乙说：“你不会是最差的”，则5人的名次排列可能有__________种（用数
字作答）．
（16）三角形的面积等于
（c为三角形的周长，r为其那内切圆半径），类比这一结论，用于研
究三棱锥的体积，用三棱锥的全面积S和其内切球半径R表示其体积V=___________．
三、解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。
（17）（本小题满分12分）
已知
．
（Ⅰ）求函数的周期；
（Ⅱ）若在上的最大值是4，求a的值．
（18）（本小题满分12分）
数列
的前三项为1，3，6，它是由一个等比数列和一个首项为零的等差数列
的对应项相加而得到．
（Ⅰ）求、的通项公式；
（Ⅱ）求数列的前n项和．
（19）（本小题满分12分）
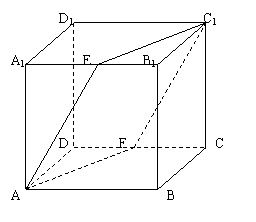如图，在棱长为1的正方体
中，
E、F分别是
、
的中点．
（Ⅰ）求二面角
的大小；
（Ⅱ）求点B到面
的距离．
（20）（本小题满分12分）
已知某种从太空飞船中带回的植物种子成功发芽的概率为，植物研究所分两个小组开展该种子发芽试验，每次试验种下一粒种子．
（Ⅰ）第一小组做了3次试验，求至少2次发芽成功的概率；
（Ⅱ）第二小组做了若干次发芽试验，若在一次试验中种子成功发芽即终止试验，否则继续下去，直到种籽发芽成功为止．
（文科做）求试验次数为3次的概率．
（理科做）若试验次数最多不超过3次，求试验次数
的期望．
（21）（本小题满分12分）
设
分别是x、y轴正方向上的单位向量)，且
．
（Ⅰ）求点
的轨迹C的方程；
（Ⅱ）过点(4，0)作直线l交曲线C于A、B两点，设
，求证：四边形OAPB
为矩形．
（22）（本小题满分14分）
（文科做Ⅰ、Ⅱ；理科全做）
对于函数
，若同时满足下列条件：
①在D上为单调函数；②存在区间
值域也是
；
则称为D上的闭函数．
（Ⅰ）求闭函数
符合条件②的区间；
（Ⅱ）若
，判断是否是闭函数；
（Ⅲ）若
是闭函数，求实数k的取值范围．
高三年级调研考试
数学参考答案及评分标准
一、CC(C)ABB DCCBB A(A)B
二、（13）15； （14）148； （15）54； （16）
．
三、（17）解：（Ⅰ）∵
∴函数的周期为
（Ⅱ）由
∴当
（18）解：（Ⅰ）设等差数列的公差为d，等比数列的公比为q，依题设可得
，解得
∴
（Ⅱ）的前n项和为
的前n项和为
∴
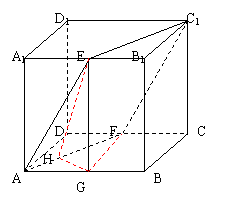（19）解：（Ⅰ）如图，取AB中点，并过点G作GH⊥AF
于H，连EH，则由EG⊥平面ABCD可知
GH为直线EH在平面ABCD内的射影，
由三垂线定理可得，EH⊥AF，所以∠EHG
为二面角的平面角．
连GF，在△AGF中，
由面积相等可得
所以，在Rt△EHG中，
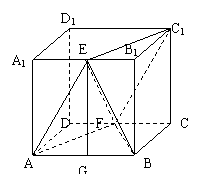（Ⅱ）方法一：连BE、BF、EF，则点B到平
面AEC1F的距离就是以B为顶点，AEF
为底面的三棱锥的高h．
在△AEF中，易知
又四边形AEC1F是平行四边形，所以平行四边
形AEC1F是菱形．
∴
由体积相等知，
，即
∴
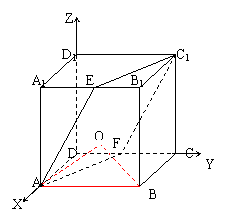方法二：过点B作BQ⊥平面AEC1F于Q，
连AQ，则BQ即为点B到平面AEC1F的距
离．
如图，建立空间直角坐标系，且可得
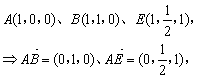
设平面AEC1F的一个法向量为
则由
∴
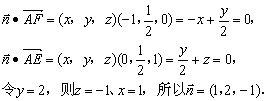
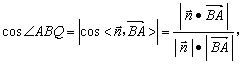
∴在Rt△ABQ中，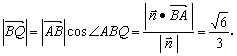
（20）解：（Ⅰ）依题设可知，植物种子成功发芽的概率
则3次试验，至少2次发芽的
概率
（Ⅱ）（文科做）依题设可知，记
，则
，
∴
（理科做）依题设可知，
则
∴
|
|
|
|
|
|
（21）解：（Ⅰ）依题设可知，
化简得
|
（Ⅱ）由
四边形OAPB是
平行四边形．
当l⊥x轴时，由
∴
，显然合题意；
当l不垂直于x轴时，设直线l的方程为
则由
∴
将A、B两点坐标代入直线l的方程中，得
∴
∴OA⊥OB，又四边形OAPB是平行四边形，
∴四边形OAPB是矩形．
综上可知，四边形OAPB是矩形．
（22）解：（Ⅰ）依题设可知，在
上是单调递减，因此，要使其在上
是闭函数，则须满足
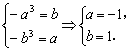
∴闭函数符合条件的区间是
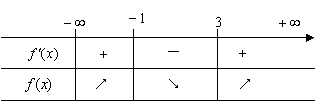（Ⅱ）由
所以
由上表可知，在
上单调递减，且
∴不是闭函数．
（Ⅲ）设函数
由函数在
上单调递增可知，函数在上也单调递增，所以
令
∴满足题意的k的取值范围是