高三年级数学第二次阶段性测试
数 学 试 卷（A卷）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
第Ⅰ卷（选择题 共60分）
一、选择题：（每题5分，共60分）
1．已知集合A={0，2，3}，B={
、
}，则B的子集的个数是 （ ）
A．4 B．8 C．16 D．15
2．
的值等于 （ ） A．
B．－ C．－
D．
3．下面四个结论：①偶函数的图象一定与y轴相交；②奇函数的图象一定通过原点；③偶
函数的图象关于y轴对称；④既是奇函数、又是偶函数的函数一定是
其
中正确的命题的个数是 （ ）
A．1个 B．2个 C．3个 D．4个
4．在等差数列1，4，7，……中，5995是它的 （ ）
A．第2005项 B．第2003项 C．第2001项 D．第1999项
5．设集合
，
，那么“
”是“
”
的 （ ）
A．充分条件但非必要条件 B．必要条件但非充分条件
C．充分必要条件 D．非充分条件也非必要条件
6．函数
的单调递增区间是 （ ） A．[1，2] B．[2，3] C．(－∞，2] D．[2，+∞）
7．已知等比数列的公比是2，且前4项的和是1，那么前8项之和为 （ ）
A．15 B．17 C．19 D．21
8．关于函数
，有下列命题
①由
的整数倍；
②
的表达式可改写为
；
③的图象关于点
对称；
④的图象关于直线
对称；
其中正确命题的序号是 （ ）
A．①② B．②③ C．①③ D．②④
9．关于x的方程
，只有负根而无正根，则a的取值范围是 （ ）
A．（－1，+∞） B．（1，+∞） C．
D．（－1，1）
10．如果奇函数
在区间[3，7]上是增函数，且最小值为5，那么f(x)在[－7，－3]上是（ ）
A．增函数且最小值为－5 B．增函数且最大值为－5
C．减函数且最小值为－5 D．减函数且最大值为－5
11．要得到函数
的图象，可将
的图象 （ ）
A．向左平移
个单位 B．向右平移个单位
C．向左平移
个单位 D．向右平移个单位
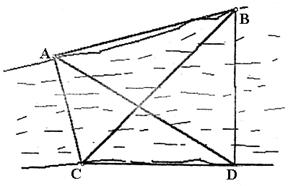
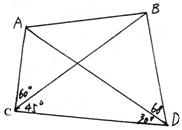
12．如图，要测量河对岸A、B两点间的距离，今沿河岸选取相距40米的C、D两点，测得
∠ACB=60°，∠BCD=45°，∠ADB=60°，∠ADC=30°，则AB的距离是 （ ）
A．20
B．20
C．20
D．40
|
第Ⅱ卷（非选择题 满分90分）
二、填空题（每题4分，共16分）
13．函数
的定义域为
.
14．在2和30之间插入两个正数，使前三个数成等比数列，后三个等差数列，则插入的两
个数分别是 .
15．已知
.
16．函数
在
上的最大值是
.
三、解答题（本大题共6小题，共74分）
17．（本小题12分）
求函数
的最小正周期.
18．（本小题12分）
一出租车司机从饭店到火车站途中有六个交通岗，假设他在各交通岗到红灯这一事件是
相互独立的，并且概率都是
（1）求这位司机遇到红灯前，已经通过了两个交通岗的概率；
（2）求这位司机在途中遇到红灯数ξ的期望和方差。
19．（本小题12分）
数列
的通项公式
（1）求：f(1)、f(2)、f(3)、f(4)的值；
（2）由上述结果推测出计算f(n)的公式，并用数学归纳法加以证明.
20．（本小题满分12分）
产品进入市场，满足的销售规律是价格越高，销售量越少。若某产品的价格为每吨p万元，销售量为q吨，则p与q满足关系
，
（1）若该产品在某地市场被一个公司垄断，试说明该公司为获得最大收入，不会一味追求价格的提高，并求出收入最大时该产品的价格；
（2）若该产品由甲、乙两家公司销售，它们的销售量分别记作q甲、q乙，于是
p=30－（q甲+q乙），若乙公司的销售量为10吨，请问甲公司销售量为多少时，其收入最大？
（3）两个公司在市场上相互竞争与联合垄断相比，哪一种情况对购买这种产品的消费者不利？请证明你的结论。
21．（本小题12分）
函数是偶函数，且是周期为2的周期函数，当x∈[2，3]时，
，在的图象上有两点A、B，它们的纵坐标相等，横坐标都在区间[1，3]上，定点C的坐标为（0,a）（其中a>2），求△ABC面积的最大值.
22．（本小题满分14分）
已知
，
（1）设
的通项；
（2）求
；
（3）设
是否存在整数m，对一切n∈N*，都有
成立？若存在，求出m的最小值；若不存在，请说明理由.
高三数学（A卷）参考答案
一、选择题（每题5分，共60分）
1.C 2.C 3.A 4.D 5.B 6.D 7.B 8.B 9.C 10.B 11.C 12.C
1．易知B={0，4，6，9}，∴B的子集数为24=16。
2．
=
.
3．偶函数的图象关于y轴对称，但不一定与y轴相交，反例：
等，∴①错
误，③正确。奇函数的图象关于原点对称，但不一定经过原点，反例：
，∴②错
误。若
既是奇函数又是偶函灵敏，由定义可得f(x)=0，但未必
（只要定义
域关于原点对称就可以）。
4．易知
得n=1999。
5．
，则x不一定属于P，即x不一定属于M∩P，故充分性不成立；若
，必要性成立。
6．
是减函数，∴函数
的单调递增区间是函数y=－3+4x－x2的单
调递减区间，而y=－3+4x－x2的单调递减区间是
。
7．
∴
8．函数
的最小正周期T=π，由相邻两个零点的横坐标间的距离是
，知①错；利用诱导公式得
知②正确；由于曲线f(x)与x轴的每个交点都是它的对称中心，将
代入得
因此点（－
）是f(x)图象的一个对称中心，故
命题③正确；曲线f(x)的对称必经过图象的最高点或最低点，且与y轴平行，而
时
y=0，点（－）不是最高点也不是最低点，故直线
不是图象的对称轴，因此④
不正确。
9．显然
∴
∴仅有负根时
1。（也可用图象解答）。
10．因奇函数在[3，7]和[－7，－3]上有相同的单调性，所以f(x)在[－7，－3]上也是增函数，所以排除两种可能，又奇函数在[3，7]有最小值5，所以在[－7，－3]有最大值－5。
11．
∴这是由y=tan2x向左平移
|
个单位而得。
12．在△ACD中，由正弦定理：
在△BCD中，由正弦定理：
.
在△ABC中由余弦定理得AB=20
.
二、填空题（每小题4分，共16分）
13．
14．6和18 15．
16．1
13．由
知真数大于零，即
14．设这两个数为2q，2q2，则有4q2=2q+30，∴q1=3，q2=
（舍），∴这两个数为6和18。
15．两边取以2为底的对数：
. ∴
∴
∴
16．对x求导数：
=
在
，令
=0，可解得x=0. 而f(0)=1，
∴最大值为1.
三、解答题（本大题共6小题，共74分）
17．（本小题12分）
解：
所以最小正周期
.
18．（本小题12分）
解：（1）因为这位司机第一、二个交通岗未遇到红灯，在第三个交通岗遇到红灯，所以
P=
（2）易知
∴
19．（本小题12分）
解：（1）
（2）推测
下面用数学归纳法证明：
①当n=1时，
∴等式成立.②假设n=k+1时等式成立∴即
则
②当n=k+1时，有
=
当n=k+1时，当n=k+1时，等式
也成立，由①、②知对任意正整数n，
都成立.
20．（本小题满分12分）
解：（1）设该公司收入为S，则S=pq，∵p+q=30，∴S=pq
当p=q=15时，S=225，这时公司收入最大，∴公司不会无限提高价格.
（2）设甲公司收入为S甲，∵p+q甲+q乙=30，q乙=10， ∴p+q甲=20，
与（1）同理知p=q甲=10时，S甲=100，这是S甲的最大值，即甲公司的销量为10吨（与乙相等）时收入最多.
（3）对消费者是否有利主要是两个指标：产品价格和销量，如产品价格高且销量小对消费者不利. 设甲、乙联合垄断市场，这种情况相当于（1），两公司为追求最大收入，产品的市场价格15万元，总销量15吨，若不允许甲、乙联合垄断市场，设q乙>0，又
p+ q甲=30－q乙，则
S甲在p=q甲=
时最大，易见p=
<15. 显然，这时的产品市场价比垄断时低，还可看到，非垄断比垄断时的产品销量也大，事实上，q甲+q乙=30－9=30－
=
>15.
综上可知，垄断对消费者不利.
21．（本小题12分）
解：如图，∵f(x)是以2为周期的周期函数，
∴当
（平移），∵f(x)是偶函数，
∴当x∈[－1，0]时，
当x∈[1，2]时，f(x)=f(x－2)=－(x－2)+1=－x+3（平移）. 设A、B的纵坐标为t（1≤t≤2），并设A在B的左边，则A、B的横坐标分别为3－t，t+1，则AB=（t+1）－（3－t）=2t－2，△ABC的面积为
令
得
当
，即2＜a≤3时，S有最大值
当
，即a＞3时，
，函数单调增，S有最大值S（2）=a－2.
[这里可将S配方；S=
也可直接用二次函数理论得出].
22．（本小题满分14分）
解：（1）
的值域y>0，解得
知
是等差数列（n∈N*）.
所以，
（2）
=
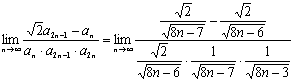
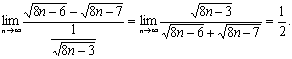
（3）
考虑
所以，
是递减数列，b1是最大的，
由于
所以mmin=8.