高三年级数学第一学期第二次测评试卷
数学（文）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。满分150分，考试时间120分钟。
第Ⅰ卷（选择题 共60分）
一、选择题（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）
1．设
，且
，则
= （ ）
A．
B．
C．
D．
2．设向量
（ ）
A．
B．
C．－ D．－
3．在等差数列
中，已知a3=2，则该数列的前5项和为 （ ）
A．10 B．16 C．20 D．32
4．已知两点P（4，－9），Q（－2，3），则直线PQ与y轴的交点分
所成的比为（ ）
A．
B． C．2 D．3
5．已知过原点的直线与圆
相切，切点在第三象限，则该直线方程为（ ）
A．
B．
C．
D．
6．不等式
的解集为 （ ）
A．
B．
C．
D．以上均不对
7．已知Sn是等差数列的前n项和，S5<S6，S6=S7，S7>S8，则下列结论中错误的是（ ）
A．d<0 B．a7=0
C．S9>S5 D．S6与S7均为Sn的最大值
8．已知θ∈R，则直线
的倾斜角的取值范围是 （ ）
A．[0°，30°] B．
C．[0°，30°]∪ D．[30°，150°]
9．已知两点M（－2，0），N（2，0），点P满足
=12，则点P的轨迹方程为（ ）
A．
B．
C．
D．
10．若
则 （ ）
A．R<P<Q B．P<R<Q C．Q<P<R D．P<Q<R
11．已知△ABC的三个顶点的A、B、C及平面内一点P满足
，下列结论中正确的是 （ ）
A．P在△ABC内部 B．P在△ABC外部
C．P在AB边所在直线上 D．P是AC边的一个三等分点
12．某城市郊区冬季种植番茄供应城市市场，当市场价格上涨时，市场供给量增加，市场需求量减少，具体调查结果如下表：
表（1）市场售价与供给量的关系 表（2）市场售价与需求量的关系
则市场供需平衡（即供给量和需求量相等时的单价）所在区间为 （ ）
A．（2.3，2.6） B．（2.4，2.6） C．（2.6，2.8） D．（2.8，2.9）
第Ⅱ卷（非选择题 共90分）
二、填空题（本大题共4小题，每小题4分，共16分，把答案填在题中横线上）
13．已知函数
满足：对任意实数x1，x2，当x1<x2时，有
，写出一个满足上述条件的函数
.
14．设S为平面内以A（4，1），B（－1，6），C（－3，2）为顶点的三角形区域（包含边界），P（x，y）为S内一点，则t=4x－3y的最小值为 .
15．若a，b，a+b成等差数列，a，b，ab成等比数列，则a，b的等比中项是 .
16．国家规定个人稿费纳税办法是：不超过800元的不纳税；超过800 元而不超过4000元的按超过800元部分的14%纳税；超过4000元的按全部稿酬的11%纳税.已知某人出版一本书，共纳税420元时，这个人应得稿费（扣税前）为 元.
三、解答题（本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤）
17．（本小题满分12分）
解关于x的不等式
18．（本小题满分12分）
已知与圆C：
相切的直线l交x轴、y轴于A、B两点，O为坐标原点，设OA=a，OB=b（a>2,b>2）.
（1）求证：圆C与直线l相切的充要条件是
；
（2）求线段AB中点M的轨迹方程.
19．（本小题满分12分）
已知向量
向量
与向量
夹角为
，且
.
（1）求向量；
（2）若向量与向量
=（1，0）的夹角为
，求2+
的值.
20．（本小题满分12分）
已知直线l方程为
（1）求证：不论m为何值，直线l必过定点M；
（2）过点M引直线l1，使它与两坐标轴的负半轴所围成的三角形面积最小，求直线l1的方程.
21．（本小题满分12分）
某公司取消福利分房和公费医疗，实行年薪制工资结构改革.该公司从2003年起，每人
的工资由三个项目组成，并按下表规定实施：
| 项 目 | 金额（元/人，年） | 计 算 方 法 |
| 基础工资 | 10000 | 考虑物价因素，从2003年（含2003年）起每年递增10%（与工龄无关） |
| 住房补贴 | 400 | 按职工到公司年限计算，每工作一年补贴400元 |
| 医 疗 费 | 1600 | 固定不变 |
如果该公司今年年初有5位职工，计划从明年起每年年初新招5名职工.
（1）若今年（2003年）算第一年，试把第n年该公司付给职工工资总额y（万元）表示成年限n的函数；
（2）试判断公司每年发给职工的工资总额中，住房补贴和医疗费的总和能否超过基础工资总额的20%，请说明理由.
22．（本小题满分14分）
如图n2个（n≥4）正数排成n行n列方阵，其中每一行的数都成等差数列，每一列的数
都成等比数列，并且所有公比都等于q.若
（1）求公比q的值； a11 a12 a13… a1n
（2）求
的值；
a21 a22 a23… a2n
（3）记第k行各项和为Ak，求A1及 … … ……
的通项公式
.
an1 an2 an3… ann
数学（文）参考答案
一、选择题（每小题5分，共60分）
1.B 2.A 3.A 4.C 5.C 6.B 7.C 8.C 9.B 10.D 11.D 12.C
二、填空题（每小题4分，共16分）
13．
（底数大于1的指数函数均可） 14．－22 15．
16．3800
三、解答题（共74分）
17．（本小题满分12分）
解：原不等式可化为
即
……3分
∵a<1，∵（x－2）
………………4分
当
时，即0<a<1时，解集为
…………6分
当
时，即a=0时，解集为
；………………9分
当
时，即a<0时，解集为
…………12分
18．（本小题满分12分）
证明（1）圆C：
………………1分
直线l的方程为
…………3分
∵l与圆C相切 ∴1=
…………6分
∴ 
即（
）（b－2）=2.…………8分
（2）设AB中点为M（x，y）.
则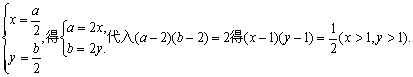
…………12分
19．（本小题满分12分）
解：（1）设
，有
① ………………2分
由
夹角为，有
.
∴
②………………4分
由①②解得
∴即
或
…………6分
（2）由
垂直知…………7分
…………10分
∴
…………12分
20．（本小题满分12分）
解：（1）原方程整理得：
由
∴不论m为何值，直线必过定点M（－1，－2）.…………4分
（2）设直线l1的方程为y=
令
…………6分
∴
…………10分
当且仅当
即k=－2时，三角形面积最小.
则直线l1的方程为
………………12分
21．（本小题满分12分）
解：（1）依题意：第n年共有5n个职工，那么基础工资总额为
（万元），
…………2分
医疗费总额为5n×0.16=
（万元），…………4分
住房补贴为5×0.04n+5×0.04(n－1)+……+5×0.04×2+5×0.04=5×0.04(1+2+3+…+n)
=0.2×
（万元）.
∴
………………6分
（2）假设可以超过，则
…………8分
即
………………10分
由函数
的图象知，上面不等式不能成立.
故住房补贴和医疗费总和不会超过基础工资总额的20%.…………12分
22．（本小题满分14分）
解：（1）设第一行公差为d，各列公比为q.
…………1分 
………2分
∴
…………6分
（2）
…………8分
（3）
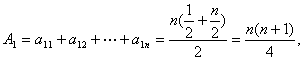
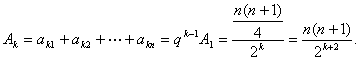…………14分