高考数学全国普通高等学校招生统一考试4
考生注意：本试卷共有22道试题，满分150分。
一、填空题（本大题满分48分）本大题共有12题，只要求直接填写结果，每个空格填对得4分，否则一律得零分。
1．已知向量
、
，若
，则
。
2．函数
的定义域为 。
3．圆锥曲线
的焦点坐标是
。
4．计算：
。
5．已知
的反函数为
，若
的图象经过点
，则
。
6．根据上海市人大十一届三次会议上的市政府工作报告，1999年上海市完成GDP（GDP是指国内生产总值）4035亿元，2000年上海市GDP预期增长9%，市委、市府提出本市常住人口每年的自然增长率将控制在0.08%，若GDP与人口均按这样的速度增长，则要使本市年人均GDP达到或超过1999年的2倍，至少需 年。
（按：1999年本市常住人口总数约1300万）
7．命题A：底面为正三角形，且顶点在底面的射影为底面中心的三棱锥是正三棱锥，命题A的等价命题B可以是：底面为正三角形，且
的三棱锥是正三棱锥。
8．设函数
是最小正周期为2的偶函数，它在区间[0，1]上的图象为如图所示的线段AB，则在区间[1，2]上，
=
。
9．在二项式
的展开式中，系数是小的项的系数为
。（结果用数值表示）
10．有红、黄、蓝三种颜色的旗帜各3面，在每种颜色的3面旗帜上分别标上号码1、2和3，现任取出3面，它们的颜色与号码不相同的概率是 。
11．图中阴影部分的点满足不等式组
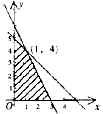
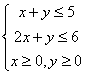，在这些点中，使目标函数
取得最大
值的点的坐标是 。
12．在等差数列
中，若
，则有等式
成立，类比上述性质，相应地：在等比数列
中，若
，则有等式
成立。
二、选择题（本大题满分16分）本大题共有4题，每题都给出代号为A、B、C、D的四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分。
13．函数
是
（A）增函数 （B）减函数 （C）偶函数 （D）奇函数
[答]（ ）
14．设有不同的直线
、
和不同的平面、
、
，给出下列三个命题：
（1）若
，
，则
。
（2）若，
，则。
（3）若
，
，则。
其中正确的个数是
（A）0 （B）1 （C）2 （D）3
[答]（ ）
15．若集合
是
（A）
（B）
（C）
（D）有限集
[答]（ ）
16．下列命题中正确的命题是
（A）若点
为角终边上一点，则
。
（B）同时满足
的角有且只有一个。
（C）当
时，
的值恒正。
（D）三角方程
的解集为
。
三、解答题（本大题满分86分）本大题共有6题，解答下列各题必须写出必要的步骤
17．（本题满分12分）
已知椭圆C的焦点分别为
和
，长轴长为6，设直线
交椭圆C于A、B两点，求线段AB的中点坐标。
[解]
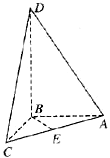
18．（本题满分12分）
如图所示四面体ABCD中，AB、BC、BD两两互相垂直，且AB=BC=2，E是AC中点，异面直线AD与BE所成的角的大小为
，求四面体ABCD的体积。
[解]
19．（本题满分14分）本题共有2个小题，第1个小题满分6分，第2小题满分8分。
已知函数
。
（1）当
时，求函数的最小值。
（2）若对任意
，
恒成立，试求实数的取值范围。
[解]（1）
[解]（2）
20．（本题满分14分）本题共有2个小题，第1小题满分4分，第2小题满分10分。
根据指令
，机器人在平面上能完成下列动作：先原地旋转角度
（为正时，按逆时针方向旋转，为负时，按顺时针方向旋转－），再朝其面对的方向沿直线行走距离
。
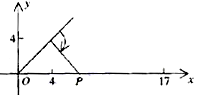
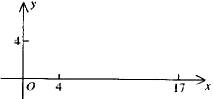（1）现机器人在直角坐标系的坐标原点，且面对
轴正方向，试给机器人下一个指令，使其移动到点（4，4）。
（2）机器人在完成该指令后，发现在点（17，0）处有一小球正向坐标原点作匀速直线滚动，已知小球滚动的速度为机器人直线行走速度的2倍，若忽略机器人原地旋转所需的时间，问机器人最快可在何处截住小球？并给出机器人截住小球所需的指令（结果精确到小数点后两位）。
[解]（1）
[解]（2）
21．（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分。
在XOY平面上有一点列
对每个自然数
，点
位于函数
的图象上，且点，点
与点
构成一个以为顶点的等腰三角形
（1）求点的纵坐标的表达式；
（2）若对每个自然数，以
，
，
为边长能构成一个三角形，求的取值范围；
（3）设
，若取（2）中确定的范围内的最小整数，问数列
前多少项的和最大？试说明理由。
[解]（1）
[解]（2）
[解]（3）
22．（本题满分18分）本题共有3个小题，第1小题满分5分，第2小题满分5分，第3小题满分8分。
已知复数
和，其中
均为实数，
为虚数单位，且对于任意复数
，有
，
。
（1）试求
的值，并分别写出
和
用、
表示的关系式：
（2）将（、）用为点
的坐标，(、)作为点
的坐标，上述关系式可以看作是坐标平面上点的一个变换：它将平面上的点变到这一平面上的点。
已知点经该变换后得到的点的坐标为
，试求点的坐标；
（3）若直线
上的任一点经上述变换后得到的点仍在该直线上，试求
的值。
[解]（1）
[解]（2）
[解]（3）
全国普通高等学校招生统一考试
答案要点及评分标准
说明
1．本解答列出试题的一种或几种解法，如果考生的解法与所列解法不同，可参照角答中评分标准的精神进行评分。
2．评阅试卷，应坚持每题评阅到底，不要因为考生的解答中出现错误而中断对该题的评阅，当考生的解答在某一步出现错误，影响了后继部分，但该步以后不解答未改变这一题的内容和难度时，可视影响程度决定反面部分的给分，这时原则上不应超过后面部分应给分数之半，如果有较严重的概念性错误，就不给分。
3．第17题至第22题中左端所注的分数，表示考生正确做到这一步应得的该题的累加分数。给分或扣分均以1分为单位。
解答
一、（第1题至第12题）每一题正确的给4分，否则一律得零分。
1．4 2．
3．（－4，0），（6，0）
4．
5．1 6．9 7．侧棱相等/侧棱与底面所成角相等/…… 8．
9．－462 10．
11．（0，5）
12．
二、（第13题至第16题）每一题正确的给4分。
| 题号 | 13 | 14 | 15 | 16 |
| 代号 | C | A | A | D |
三、（第17题至第22题）
17．[解]设椭圆C的方程为
…（2分）
由题意
，
，于是
。
∴椭圆C的方程为
…（4分）
由
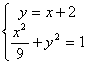得
因为该二次方程的判别
，所以直线与椭圆有两个不同交点。 …（8分）
设
则
，
故线段AB的中点坐标为
…（12分）
18．[解法一]如图建立空间直角坐标系， …（2分）
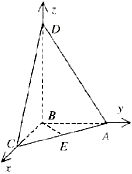由题意，有
，
，
设D点的坐标为
，
则
，
…（6分）
则
，
且
所成的角的大小为。
∴
，
得
，故BD的长度是4， …（10分）
又
，
因此四面体ABCD的体积是
，
…（12分）
[解法二]过A引BE的平行线，交CB的延长线于F，∠DAF是异面直线BE与AD所成的角。
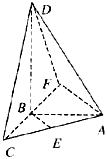∴∠DAF=，
…（4分）
∵E是AC的中点，∴B是CF的中点，
AF=2BE=
。
…（6分）
又BF，BA分别是DF，DA的射影，且BF=BC=BA，
∴DF=DA …（8分）
三角形ADF是等腰三角形，
AD=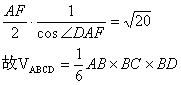
，
…（10分）
因此四面体ABCD的体积是
…（12分）
19．[解]（1）当时，
，
在区间[
]上为增函数，
…（3分）
在区间[]上的最小值为
…（6分）
（2）[解法一]在区间的[]上，
的恒成立
恒成立，
…（8分）
设
，
递增，∴当
时，
， …（12分）
于是当且仅当
时，函数恒成立，
故
…（14分）
（2）[解法二]
，
当
时，函数的值恒为正，
…（8分）
当
时，函数递增，
故当时，
，
…（12分）
于是当且仅当时，
函数恒成立，
故
…（14分）
20．[解]（1）
，
，
得指令为
，
…（4分）
（2）设机器人最快在点
处截住小球…（6分）
则因为小球速度是机器人速度的2倍，所以在相同时间内有
…（8分）
即
得
。
∵要求机器人最快地去截住小球，即小球滚动距离最短，
∴
故机器人最快可在点
处截住小球，
…（10分）
所给的指令为
…（14分）
21．[解]（1）由题意，
，
…（4分）
[解]（2）∵函数
递减，
∴对每个自然数，有＞＞，
则以，，为边长能构成一个三角形的充要条件是+＞，
即
，
…（7分）
解得
，
∴
…（10分）
[解]（3）∵，
∴
，
，
…（12分）
于是
,
数列是一个递减的等差数列。
因此，当且仅当
，且
时，数列的前项的和最大。
由
，
得
，
∴
…（16分）
22．[解]（1）由题设，
，
于是由
…（3分）
因此由
，
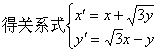…（5分）
[解]（2）由题意，有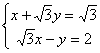
…（7分）
，
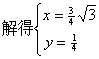即P点的坐标为
。
…（10分）
[解]（3）∵直线上的任意点P
，其经变换后的点
仍在该直线上，
∴
，
即
…（13分）
[解法一]∵当
时，
，
不是同一条直线，
∴
，
于是
，
…（16分）
即
解得
…（18分）
[解法二]取直线
上的点
。
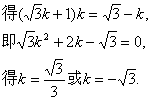…（16分）
经检验，
确实满足条件
…（18分）