高考数学试题3
第I卷(选择题 60分)
参考公式:
三角函数的积化和差公式
![]()
![]()
![]()
![]()
正棱台、圆台的侧面积公式
![]()
其中![]() 、
、![]() 分别表示上、下底面周长,
分别表示上、下底面周长,![]() 表示斜高或母线长
表示斜高或母线长
台体的体积公式
![]()
其中![]() 、
、![]() 分别表示上、下底面积,
分别表示上、下底面积,![]() 表示高
表示高
一、 选择题:本大题共12小题;第每小题5分,共60分。在每小题给出的
四个选项中,只有一项是符合题目要求的。
(1)
已知集合A=![]() ,那么A的真子集的个数是
,那么A的真子集的个数是
(A)3 (B)16 (C)15 (D)4
(2)
在复平面内,把复数![]() 对应的向量按顺时针方向旋转
对应的向量按顺时针方向旋转![]() ,所得向量对应的复数是
,所得向量对应的复数是
(A)![]() (B)
(B)![]() (C)2
(C)2![]() (D)3
(D)3![]()
(3)
一个长方体共一项点的三个面的面积分别是![]() ,
,![]() ,
,![]() ,这个长方体
,这个长方体
对角线的长是
(A)6 (B)3![]() (C)2
(C)2![]() (D)
(D)![]()
(4)已知![]() ,那么下列命题成立的是
,那么下列命题成立的是
(A)若![]() 、
、![]() 是第三象限角,则
是第三象限角,则![]()
(B)若![]() 、
、![]() 是第二象限角,则
是第二象限角,则![]()
(C)若![]() 、
、![]() 是第三象限角,则
是第三象限角,则![]()
(D)若![]() 、
、![]() 是第四象限角,则
是第四象限角,则![]()
(5)函数![]() 的部分图象是
的部分图象是
 |
(6)依法纳税是公民的义务。按规定,全月工资、薪金所得不超过 800元的部分不必纳税,超过800元的部分,按下列分段累进计算税款:
| 工资、薪金所得超过800元的部分中 | 税率 |
| 不超过500元的部分 | 5% |
| 超过500元至2000元的部分 | 10% |
| 超过2000元至5000元的部分 | 15% |
| … | … |
某人一月份应交纳此项税款26.78元,则他的当月工资、薪金所得介于
(A) 1200~1500元 (B)900~1200元
(C)800~900元 (D)1500~2800元
(7)若![]() ,P=
,P=![]() ,Q=
,Q=![]() ,R=
,R=![]() ,则
,则
(A)Q ![]() P
P![]() R
(B)P
R
(B)P![]() Q
Q ![]() R
R
(C)R![]() P
P![]() Q
(D)P
Q
(D)P ![]() R
R![]() Q
Q
(8)以极坐标系中的点![]() 为圆心,1为半径的圆的方程是
为圆心,1为半径的圆的方程是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(9)一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比
是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
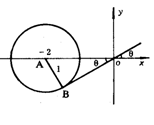
(10)过原点的直线与圆![]() 相切,若切点在第三象限,则该直
相切,若切点在第三象限,则该直
线的方程是
(A)y=![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(11)过抛物线![]() 的焦点F作一条直线交抛物线于P、Q两点,若线
的焦点F作一条直线交抛物线于P、Q两点,若线
段PF与FQ的长分别是![]() 、
、![]() ,则
,则![]() 等于
等于
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
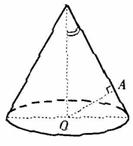
(12)如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲
面将圆锥分成体积相等的两部分,则母线与轴的夹角的余弦值为
 (A)
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
第II卷(非选择题 90分)
二.填空题:本大题共4小题;每小题4分,共16分,把答案填在题中横
线上。
(13)乒乓球队的10名队员中有3名主力队员,派5名参加比赛。3名主力
队员要安排在第一、三、五位置,其余7名队员选2名安排在第二、四
位置,那么不同的出场安排共有_____种(用数字作答)。
(14)椭圆![]() 的焦点为
的焦点为![]() 、
、![]() ,点P为其上的动点,当
,点P为其上的动点,当![]() 为钝角
为钝角
时,点P横坐标的取值范围是________。
(15)设![]() 是首项为1的正项数列,且
是首项为1的正项数列,且![]() (
(![]() =1,2,
=1,2,
3,…),则它的通项公式是![]() =________。
=________。
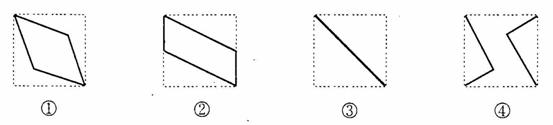
(16)如图,E、F分别为正方体的面![]() 、面
、面![]() 的中心,则四边形
的中心,则四边形![]() 在该正方体的面上的射影可能是_______。(要求:把可能的图的 序号都填上)
在该正方体的面上的射影可能是_______。(要求:把可能的图的 序号都填上)
|
|
三、解答题:本大题共6小题;共74分,解答应写出文字说明、证明过程或
演算步骤。
(17)(本小题满分12分)
已知函数![]()
![]() ,
,![]() 。
。
(I)当函数![]() 取得最大值时,求自变量
取得最大值时,求自变量![]() 的集合;
的集合;
(II)该函数的图象可由![]() 的图象经过怎样的平移和伸缩变换
的图象经过怎样的平移和伸缩变换
得到?
(18)(本小题12分)
设{![]() }为等比数列,
}为等比数列,![]() ,已知
,已知![]()
(Ⅰ)求数列![]() 的首项和公式比;
的首项和公式比;
(Ⅱ)求数列![]() 的通项公式。
的通项公式。
(19)(本小题满分12分)
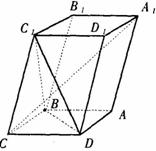 如图,已知平行六面体ABCD-
如图,已知平行六面体ABCD-![]() 的底面ABCD是菱形,且
的底面ABCD是菱形,且![]() =
=![]() 。
。
(I)证明:![]() ⊥BD;
⊥BD;
(II)当![]() 的值为多少时,能使
的值为多少时,能使![]() 平面
平面![]() ?请给出证明。
?请给出证明。
(20)(本小题满分12分)
设函数![]() ,其中
,其中![]() 。
。
 |
(I)解不等式
(II)证明:当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是单调函数。
上是单调函数。
(21)(本小题满分12分)
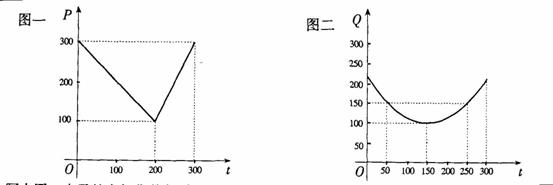
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示。
(I)写出图一表示的市场售价与时间的函数关系式P=![]() ;
;
写出图二表示的种植成本与时间的函数关系式Q=![]() ;
;
(II) 认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最
大?
(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天)
kg,时间单位:天)
(22)(本小题满分14分)
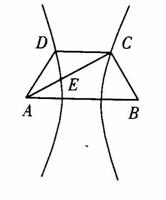 如图,已知梯形ABCD中
如图,已知梯形ABCD中![]() ,点E分有向线段
,点E分有向线段![]() 所成的比为
所成的比为![]() ,双曲线过C、D、E三点,且以A、B为焦点。当
,双曲线过C、D、E三点,且以A、B为焦点。当![]() 时,求双曲线离心率
时,求双曲线离心率![]() 的取值范围。
的取值范围。
高考
参考答案
一、选择题:
(1)
n元素的真子集有![]() 个,本题结果为
个,本题结果为![]() =15。答(C)。
=15。答(C)。
(2)
![]() 。答(B)。
。答(B)。
(3)
设长方体三度为![]() 则
则![]() 三式相乘得
三式相乘得![]() 答(B)。
答(B)。
(4)
若![]() 、
、![]() 同属于第一象限,则
同属于第一象限,则![]() ,
,![]() ;第二象限,则
;第二象限,则![]() ,
,![]() ;第三象限,则
;第三象限,则![]() ,
,![]() ;
;
第四象限,则![]() ,
,![]() 。(均假定
。(均假定![]() ,
,![]() 。)答(D)。
。)答(D)。
(5)
设![]() 则
则![]()
![]() 为奇数;又
为奇数;又![]() 时
时![]() 故答(D)。
故答(D)。
(6)
设收入为S元,税款为M元,则![]() 时,M=0;
时,M=0;![]() 时,
时,![]() 时,
时,![]() 题设
题设![]() ,故
,故![]() 答(A)。
答(A)。
(7)
由平均不等式知![]() 同理
同理![]() 答(B)。
答(B)。
(8)
所求方程是![]() 化简得
化简得![]() 答(A)。
答(A)。
(9)
设圆柱底面积半径为r,则高为![]() 全面积,侧面积
全面积,侧面积![]() 答(C)。
答(C)。
(10)圆方程为![]() 圆心为A(-2,0),半径为1,
圆心为A(-2,0),半径为1,
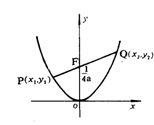 |
(11) 设PQ直线方程是
设PQ直线方程是![]() 则
则![]() 是方程
是方程![]() 的两根,
的两根,![]() 其中
其中![]() 同理
同理![]() 从而
从而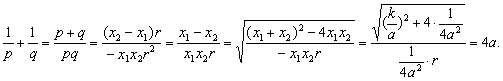 答(A)。
答(A)。
(另解)按选择题4选1的规定,本题中4个选择支都是常数,故应有 ![]() 常数。过F作
常数。过F作![]() ∥x轴,则易得
∥x轴,则易得![]() 答(A)。
答(A)。
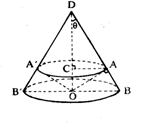 (12)如图,设
(12)如图,设![]() 则
则![]()
由题意知![]() 故知
故知![]() 答(D)。
答(D)。
二、填空题:
 (13)
(13)![]() 正确答案是252。
正确答案是252。
(14)如图,设![]() 则
则![]() 且
且![]() 是钝角
是钝角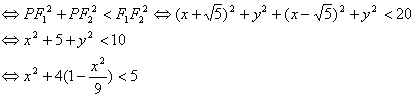
![]() 正确答案是
正确答案是![]()
(15)![]() (另解
(另解![]() 不合题意舍去),
不合题意舍去),![]() 即
即![]() 正确答案是
正确答案是![]()
(16)平行四过形![]() 投影于左、右两侧得图③,投影于上、下、前、后四侧面都得图②。正确答案是②③。
投影于左、右两侧得图③,投影于上、下、前、后四侧面都得图②。正确答案是②③。
三、解答题
(17)
解:(I)![]()
![]()
![]()
![]()
y 取得最大值必须且只需
![]()
即 ![]() ,
,![]() 。
。
所以,当函数![]() 取得最大值的自变量
取得最大值的自变量![]() 的集合为
的集合为
![]() 。
——6分
。
——6分
(II)变换的步骤是:
(i) 把函数![]() 的图象向左平移
的图象向左平移![]() ,得到函数
,得到函数
![]() 的图象;
——9分
的图象;
——9分
(ii) 令所得到的图象上各点横坐标不变,把纵坐标伸长到原来的2倍),得到函数
![]() 的图象;
的图象;
经过这样的变换就得到函数![]() 的图象。 ——12分
的图象。 ——12分
(18) 解:设等比数列![]() 的公比为q,则
的公比为q,则
![]()
∵ ![]()
(Ⅱ) 解法一:由(I)知 ![]() 故
故![]() 因此
因此![]()
![]()
![]()
![]()
![]()
![]()
解法二:设![]()
由(I)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(19)
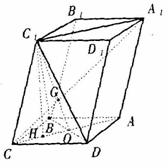 (I)证明:连结
(I)证明:连结![]() 、AC,AC和BD交于O,连结
、AC,AC和BD交于O,连结![]() 。
。
∵ 四边形ABCD是菱形,
∴ AC⊥BD,BC=CD。
又∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵ DO=OB,
∴ ![]() BD,
BD,
但 AC⊥BD,AC∩![]() =O,
=O,
∴ BD⊥平面![]() 。
。
又 ![]() 平面
平面![]() ,
,
∴ ![]() BD。
BD。
(II)当![]() 时,能使
时,能使![]() ⊥平面
⊥平面![]() 。
。
证明一:
∵ ![]() ,
,
∴ BC=CD=![]() ,
,
又 ![]() ,
,
由此可推得BD=![]() 。
。
∴ 三棱锥C- ![]() 是正三棱锥。
是正三棱锥。
设![]() 与
与![]() 相交于G。
相交于G。
∵ ![]() ∥AC,且
∥AC,且![]() ∶OC=2∶1,
∶OC=2∶1,
∴ ![]() ∶GO=2∶1。
∶GO=2∶1。
又 ![]() 是正三角形
是正三角形![]() 的BD边上的高和中线,
的BD边上的高和中线,
∴ 点G是正三角形![]() 的中心,
的中心,
∴ CG⊥平面![]() 。
。
即 ![]() ⊥平面
⊥平面![]() 。
。
证明二:
由(I)知,BD⊥平面![]() ,
,
∵ ![]()
![]() 平面
平面![]() ,∴ BD⊥
,∴ BD⊥![]() 。
。
当 ![]() 时 ,平行六面体的六个面是全等的菱形,
时 ,平行六面体的六个面是全等的菱形,
同BD⊥![]() 的证法可得
的证法可得![]() ⊥
⊥![]() 。
。
又 BD∩![]() =B,
=B,
∴![]() ⊥平面
⊥平面![]() 。
。
(20) 解:(I)不等式![]() 即
即
![]() ,
,
由此得![]() ,即
,即![]() ,其中常数
,其中常数![]() 。
。
所以,原不等式等价于
![]()
即 ![]()
所以,当![]() 时,所给不等式的解集为
时,所给不等式的解集为![]() ;
;
当![]() 时,所给不等式的解集为
时,所给不等式的解集为![]() 。
。
(II)证明:在区间![]() 上任取
上任取![]() ,
,![]() ,使得
,使得![]() <
<![]() 。
。
![]()
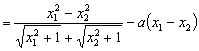
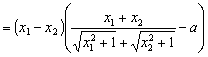 。
。
∵ ![]() ,且
,且![]() ,
,
∴ ![]() ,
,
又 ![]() ,
,
∴ ![]() ,
,
即 ![]() 。
。
所以,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是单调(递减)函数。
上是单调(递减)函数。
(21) 解:(I)由图一可得市场售价与时间的函数关系为
![]() ——2分
——2分
由图二可得种植成本与时间的函数关系为
![]() ,
, ![]() ——4分
——4分
(II)设![]() 时刻的纯收益为
时刻的纯收益为![]() ,则由题意得
,则由题意得
![]() ,
,
即 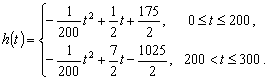 ——6分
——6分
当![]() 时,配方整理得
时,配方整理得
![]() ,
,
所以,当![]() =50时,
=50时,![]() 取得区间
取得区间![]() 上的最大值100;
上的最大值100;
当 ![]() 时,配方整理得
时,配方整理得
![]() ,
,
所以,当![]() 时,
时,![]() 取得区间
取得区间![]() 上的最大值87.5。
上的最大值87.5。
综上,由100>87.5可知,![]() 在区间
在区间![]() 上可以取最大值100,此时,
上可以取最大值100,此时, ![]() ,即从二月一日开始的第50天时,上市的西红柿纯收益最大。
,即从二月一日开始的第50天时,上市的西红柿纯收益最大。
(22)
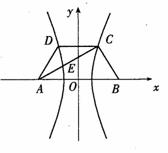 解:如图,以AB为垂直平分线为
解:如图,以AB为垂直平分线为![]() 轴,直线AB为
轴,直线AB为![]() 轴,建立直角坐标系
轴,建立直角坐标系![]() ,则CD⊥
,则CD⊥![]() 轴。
轴。
因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于![]() 轴对称。
轴对称。
依题意,记A![]() ,C
,C![]() ,E
,E![]() ,其中
,其中![]() 为双曲线的半焦距,
为双曲线的半焦距,![]() 是梯形的高。
是梯形的高。
由定比分点坐标公式得
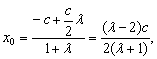
![]()
设双曲线的方程为![]() ,则离心率
,则离心率![]() 。
。
由点C、E在双曲线上,将点C,E的坐标和![]() 代入双曲线的方程,得
代入双曲线的方程,得
![]() ①
①
![]() ②
②
由①式得![]() ,③
,③
将③代入②式,整理得![]() ,
,
故
![]()
由题设![]() 得,
得,
![]()
解得![]()
故双曲线的离心率的取值范围为![]()