高三第一轮复习导数、测试

高三第一轮复习导数、测试

一、选择题（本题每题5分，共60分）

1． ，则　　　　　　　　　　　　　　　　 　　　　　　　　（　　）

　　　A． 　B．　　C．　　　D．

2．以下结论不正确的是（ 　　）

A．函数在处的导数的几何意义就是曲线在点处的切线的斜率

B．函数在开区间内每一点可导才能说该函数在该区间内可导

C．函数在的导数为-4

D．两个不同的函数与在处的导数可能相同

3．设在处可导，且，则等于　　 （　　）

A．1　　　　　　　 B．0　　　　　　　 C．3　　　　 　　　D．

4．设对于任意的，都有，则=（　　）

A．　　　　　　  B．　　　　　　  C．　　　　　　　 D．

5．函数的单调递增区间为　　　　　　　　　　　　　　　 （　 ）

A．　B． C．　D．

6．下列函数中，是极值点的函数是　　　　　　　　　　　　　　 　（　　 ）

A．　　　 B．　　　　C．　　D．

7．函数在区间[－2，3]上的最大值与最小值分别是　　 （　　）

　　 A．5，4　　　　　　　　　　 B．13，4　　　　　　　　 C．68，4　　　　　　　　 D．68，5

8．设在［０，1］上函数的图象是连续的，且，则下列关系一定成立的是　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　A．　　　　　　B．　　　　　　C．　　　　D．

9．若曲线在点P处的切线平行于直线，则点P的坐标为（　　）

　　　　A．（1，3）　　　　　　　　 B．（，3）　　　　　　　　 C．（1，0）　　　　　　　　　 D．（－1，0）

10．函数，其中为实数，当时，是 （　　）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　 　A． 增函数　B． 减函数　　　 C． 常数　　　D． 既不是增函数也不是减函数

11．下列说法正确的是（　　）

A．函数在闭区间上的极大值一定比极小值大 B．函数在闭区间上的最大值一定是极大值

C．对于，若，则无极值

D．函数在区间上一定存在最值

12．已知函数有极大值和极小值，则实数a的取值范围是（　）

　 A．　B．　 C．　　　　　　 D．

二、填空题（本题每小题4分，共16分）

13．已知函数在x=1处有极值为10，则f(2)等于　　　　　　 .

14．二次函数，则实数a的取值范是　　　　　　 .

15．曲线在点M（1，）处的切线方程是_______.

16．某质点的运动方程是，则在t=1时的瞬时速度为__　　 _____.

三、解答题（本题17—21小题每题12分，22小题14分，共74分）

17．已知为实数,且 ,其中是自然对数的底, 证明.

18．已知抛物线C₁：y=x²+2x和：y=－x²+a，如果直线l同时是C₁和C₂的切线，称l是C₁和C₂的公切线，公切线上两个切点之间的线段，称为公切线段.

　 （Ⅰ）a取什么值时，C₁和C₂有且仅有一条公切线？写出此公切线的方程；

　 （Ⅱ）若C₁和C₂有两条公切线，证明相应的两条公切线段互相平分.

　

　

19．用总长44.8m的钢条制做一个底面是等腰三角形的直三棱柱容器的框架，如果所制做容器的底面的腰长比底边长的一半长1m，那么底面的底边，腰及容器的高为多少时容器的容积最大？

（参考数据2.66²=7.0756，3.34²=11.1556）

20．设，函数的最大值为1，最小值为，求常数。

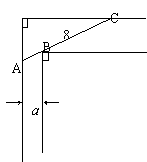21．宽为a的走廊与另一走廊垂直相连，如果长为8a的细杆能水平地通过拐角，向另一走廊的宽度至少是多少？

 

22．已知上是增函数，在[0，2]上是减函数，且方程

有三个根，它们分别为.

　　　（Ⅰ）求c的值；　　 （Ⅱ）求证　（Ⅲ）求的取值范围.

 

　

　高三第一轮复习 导数 测试 参考答案

一、1． D　2． C　3． D 4．B　5． A　 6． B　7． C　8． C　9． C　10．  A　 11．  C  12．  C

二、13． 18　　14． 　 15． 　　 16．  

三、17．  当时，要证，只要证 ，即只要证 ，

考虑函数，因为当 时， 函数在内是减函数，由于，　即.

18．（Ⅰ）函数y=x²+2x的导数y′=2x+2,曲线C₁在点P（x₁,x+2x₁）的切线方程是

y－(x+2x₁)=(2x₁+2)(x－x₁),即 y=(2x₁+2)x－x　①

函数y=－x²+a的导数y′=－2x, 曲线C₂ 在点Q（x₂,－x+a）的切线方程是

y－(－x+a)=－2x₂(x－x₂).　　y=－2x₂x+x+a .　　 ②

如果直线l是过P和Q的公切线，则①式和②式都是l的方程，

 x₁+1=－x_2,

所以　　 － x=x+a.　　消去x₂得方程　2x+2x₂+1+a=0.

若判别式△=4－4×2（1+a）=0时，即a=－时解得x₁=－，此时点P与Q重合.

即当a=－时C₁和C₂有且仅有一条公切线，由①得公切线方程为  y=x－ .

　 （Ⅱ）由（Ⅰ）可知.当a<－时C₁和C₂有两条公切线

设一条公切线上切点为：P（x₁,y₁）, 　　　　　　　 Q（x₂ , y₂ ）.　其中P在C₁上，Q在C₂上，则有

x₁+x₂=－1,　 y₁+y₂=x+2x₁+(－x+a)= x+2x₁－(x₁+1)²+a=－1+a .

线段PQ的中点为　同理，另一条公切线段P′Q′的中点也是

所以公切线段PQ和P′Q′互相平分.

19．设容器底面等腰三角形的底边长为2xm，则腰长为高为.　

设容器的容积为Vm³，底面等腰三角形底边上的高

.

　　　　　令.

　　　　 当有最大值.

　　　　　这时容器的底面等腰三角形的底边长为6m，腰长为4m，容器的高为5.6m..

20．解：令得或，

当时，；当时，；当时，。

故函数有极大值，极小值，

又，，由于，

∵，，又，故最大值为，

同理，，故最小值为

21．设细杆与另一走廊一边的夹角为，又设另一走廊的宽为y．

，　．

依题意必存在一个适当的θ值使y最小．

由. 令，得

因为只有一个极值，所以它是最小值，这时y=，即另一走廊的宽度至少是．

22．(Ⅰ)　上是增函数，在[0，2]上是减函数，

　 　∴当取到极大值，

（Ⅱ）的两个根分别为

　　　　∵函数上是减函数，.

　　　　

（Ⅲ）

　　　　

　　　　

　　　　

　　　　.
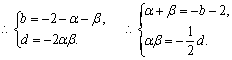