高考数学模拟试题四答案

高考数学模拟试题四NJGZ

一、选择题（每题只有一个正确答案，每小题5分，共60分）

1．已知集合，则实数a的取值

　 范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（B）

　　　 A．[1，2]　　　　　　　　B．（－1，2）　　　　　C．[－1，2]　　　　　　 D．（－2，1）

2．在数列，则该数列中相邻两项的乘积是负数的

　 是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （C）

　　　 A．　　　　　　 B．a₂₂·a₂₃　　　　　　　　 C．a₂₃·a₂₄　　　　　　　　D．a₂₄·a₂₅

3．要使函数上存在反函数，则a的取值范围是　　　　　　　　　（C）

　　　 A．　　　　　　　　 B．　　　　　　　　C．或　　D．

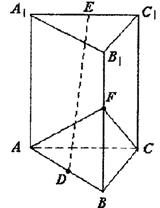
4．已知长方体ABCD－A₁B₁C₁D₁中，AB=BC=4，CC₁=2，则直线BC₁和平面DBB₁D₁所成

　 角的正弦值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（C）

　　　 A．　　　　　　　　　 B．　　　　　　　　　 C．　　　　　　　　 D．

5．函数在闭区间[－1，1]上的最大值是　　　　　　　　　　　　　　　　　　（A）

　　　 A．　　　　　　　　　　B．　　　　　　　　　　C．0　　　　　　　　　　　　D．－

6．随机变量ξ的概率分布规律为其中a是常数，则

　 的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （D）

　　　 A．　　　　　　　　　　　B．　　　　　　　　　　　C．　　　　　　　　　　　D．

7．已知点A（－2，0）及点B（0，2），C是圆x²+y²=1上一个动点，则△ABC的面积的最

　 小值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（A）

　　　 A．2　　　　　　　 B．2+　　　　　　　　C．2　　　　　　　　　　　　D．

8．从8盆不同的鲜花中选出4盆摆成一排，其中甲、乙两盆不同时展出的摆法种数为

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（A）

　　　 A．1320　　　　　　　　　 B．960　　　　　　　　　　 C．600　　　　　　　　　　 D．360

9．使不等式成立的x的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　（A）

　　　 A．（0，1）　　　　　　　B．　　　　　　　　 C．　　　　　　　 D．

10．将3种农作物都种植在如图的4块试验田里，每块种值一种

　 农作物，要求相邻的试验田不能种植同一种作物，则不同的

　 种植方法共有　　　　　　　　　　　　　　  （C）

　　　 A．6种　　　　　　　　　　B．12种　　　　　　　　　C．18种　　　　　　　　　D．24种

11．一机器狗每秒钟前进或后退一步，程度设计师让机器狗以前进3步，然后再后退2步的规律移动. 如果将此机器狗放在数轴的原点，面向正的方向，以1步的距离为1单位长，令P（n）表示第n秒时机器狗所在位置的坐标，且P（0）=0，那么下列结论中错误的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（D）

　　　 A．P（3）=3　　　　　　　　　　　　　　　　　　　　　 B．P（5）=1

　　　 C．P（101）=21　　　　　　　　　　　　　　　　　　　D．P（103）<P（104）

12．已知定义在R上的函数y=f(x)满足下列三个条件：①对任意的x∈R都有②对于任意的，都有③的图象关于y轴对称，则下列结论中，正确的是　　　　　　　　　　　　　　　　　　　　　（B）

　　　 A．　　　　　　　　　 B．

　　　 C．　　　　　　　　　 D．

二、填空题（每小题4分，共16分）

13．当=2

14．设非零复数x，y满足，则代数式的值是1.

15．（理）定义运算：，若复数满足的模等于x，则复数z对应的Z（x，y）的轨迹方程为：；

16．若函数的值域是R，则实数a的取值范围

是（0，1）∪（1，4

三、解答题（本大题共6小题，共74分）

17．（本小题满分12分）

　　　 已知A、B、C的坐标分别为A（3，0），B（0，3），C（），

　　　 （I）若求角的值；

　　　 （II）若的值.

解：（1）

 ，

.

由得.　　 又.（2）由

①又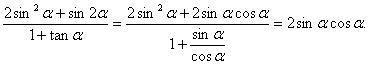由①式两分平方得

18．（本题满分12分）

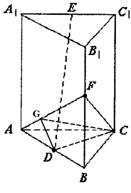
如图，正三棱柱AC₁中，AB=2，D是AB的中点，E是A₁C₁的中点，F是B₁B中点，异面直线CF与DE所成的角为90°.

　 （1）求此三棱柱的高；

　 （2）求二面角C—AF—B的大小.

解：（1）取BC、C₁C的中点分别为H、N，连结HC₁，

连结FN，交HC₁于点K，则点K为HC₁的中点，因

FN//HC，则△HMC∽△FMK，因H为BC中点

BC=AB=2，则KN=，∴

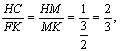
则HM=，在Rt△HCC₁，HC²=HM·HC₁，

解得HC₁=，C₁C=2.

另解：取AC中点O，以OB为x轴，OC为y轴，按右手系建立空间坐标系，设棱柱高为h，则C（0，1，0），F（），D（），E（0，0，h），

∴，由CF⊥DE，得，解得h=2.

　 （2）连CD，易得CD⊥面AA₁B₁B，作DG⊥AF，连CG，

由三垂线定理得CG⊥AF，所以∠CGD是二面角C—AF—B

的平面角，又在Rt△AFB中，AD=1，BF=1，AF=，

从而DG=∴tan∠CGD=，

故二面角C—AF—B大小为arctan.

19．（本题满分12分）

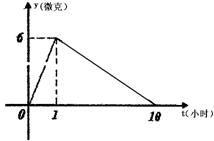
某医药研究所开发一种新药，如果成人按规定的剂量服用，据监测：服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.

　 （1）写出服药后y与t之间的函数关系式；

　 （2）据测定：每毫升血液中含药量不少于4微克时治疗疾病有效，假若某病人一天中第一次服药时间为上午7:00，问一天中怎样安排服药的时间（共4次）效果最佳？

解：（1）依题得，y=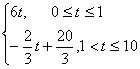

　 （2）设第二次服药时在第一次服药后t₁小时，则因而第二次服药应在11:00；

　　　　设第三次服药在第一次服药后t₂小时，则此时血液中含药量应为两次服药量的和，即有解得t₂=9小时，故第三次服药应在16:00；

　　　　设第四次服药在第一次后t₃小时（t₃>10），则此时第一次服进的药已吸收完，此时血液中含药量应为第二、三次的和，解得

　　　　t₃=13.5小时，故第四次服药应在20:30.

20．（本小题满分12分）

　 （理）设函数是定义在上的奇函数，当时为实数）.

（I）当时，求的解析式；

（II）若，试判断上的单调性，并证明你的结论；

（III）是否存在a，使得当有最大值－6？

（理）解：（I）设

　　　　 ………3分

　 （II）

　　　　

　　　　上是单调递增的.……………………………………7分

　 （III）当单调递增，

　　　　 （不合题意，舍去）

　　　　 当，……………………………………………10分

　　　　 如下表，，

x
	+	0	－
		最大值

　　　　

　　　　∴存在上有最大值－6

21．（本题满分12分）

如图，过点（1，0）的直线l与中心在原点，焦点在x轴上且离心率为的椭圆相交于A、B两点，直线过线段AB的中点M，同时椭圆上存在一点与右焦点F关于直线l对称，求直线l和椭圆的方程.

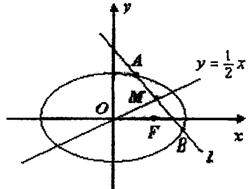
解：由题意，

 ∴椭圆方程可设为：

　  设直线l：y=k(x－1)，

显然k≠0，将直线方程代入椭圆方程：

　　

　　 整理得：　①

　　 设交点A（），B（），中点M（），而中点在直线上，

　　 ∴　∴，

　　 求得：k=－1，将k=－1代入①，其中△>0求得，点

F（c，0）关于直线l：y=－x+1的对称点（1，1－c）在椭圆上，代入椭圆方程：

∴1+2(1－c)²－2c²=0， ∴c=

∴所求椭圆为C：，直线l方程为：

22．（本题满分14分，附加题4分）

　 （Ⅰ）已知a>0，函数

　 （1）当b>0时，若对任意；

　 （2）当b>1时，证明：对任意的充要条件是；

解：（1）证明：由题设，对任意 ∵

∴　∵a>0，b>0，

　 （2）证明：必要性：对任意因此，

即　对任意

可推出　 即

充分性：因为b>1，对任意，可以推出

因为，b>1，对任意，可以推出

综上，当b>1时，对任意，的充要条件是：