高考数学模拟试题五NJGZ
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的.)
1.集合![]() ( )
( )
A.{(1,0)} B.{y0≤y≤1} C.{1,0} D.φ
2.设随机变量ξ服从正态分布![]() 则下列结论不正确的是( )
则下列结论不正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.如果![]() 等于 ( )
等于 ( )
A.2003 B.1001 C.2004 D.2002
4.若x∈R、n∈N*,定义:![]() =(-5)(-4)
=(-5)(-4)
(-3)(-2)(-1)=-120,则函数![]() 的奇偶性为 ( )
的奇偶性为 ( )
A.是偶函数而不是奇函数 B.是奇函数而不是偶函数
C.既是奇函数又是偶函数 D.既不是奇函数又不是偶函数
![]() =x·(x-9)(x-8)x(x+8)[(x-9)+19-1]=x2(x2-9)…(x2-1).
=x·(x-9)(x-8)x(x+8)[(x-9)+19-1]=x2(x2-9)…(x2-1).
5.二次函数![]() 满足
满足![]() ,又
,又![]() ,若在
,若在![]() 有最大值3,最小值1,则
有最大值3,最小值1,则![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
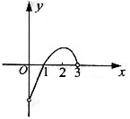 6.已知
6.已知![]() 的定义在(-3,3)上的奇函数,当0<x<3时,
的定义在(-3,3)上的奇函数,当0<x<3时,![]() 的图象如图所示,那么不等式
的图象如图所示,那么不等式![]() 的解集是
( )
的解集是
( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
7.函数![]() ,且
,且![]() )是偶函数,且在
)是偶函数,且在![]() 上单调递减,则
上单调递减,则
![]() 与
与![]() 的大小关系是 ( )
的大小关系是 ( )
A.![]() >
>![]() B.
B.![]()
![]()
![]()
C.![]()
![]()
![]() D.
D.![]() <
<![]()
8. 由等式![]()
定义![]() ,则
,则![]() 等于 ( )
等于 ( )
A.(1,2,3,4,) B.(0,3,4,0,)
C.(-1,0,2,-2) D.(0,-3,4,-1).
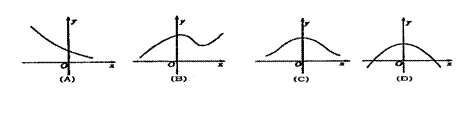
9.![]() 的部分图象大致是 ( )
的部分图象大致是 ( )
 |
|
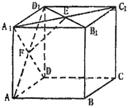
ADD1A1的中心,则EF和CD所成的角是 ( )
A.60° B.45° C.30° D.90°
11.对某种产品的6件不同正品和4件不同次品,一一进行测试,到区分出所有次品为止。
若所有次品恰好在第五次测试被全部发现,则这样的测试方法有 ( )
A.24种 B.96种 C.576种 D.720种
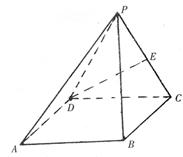
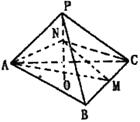 12.三棱锥P—ABC的高PO=8,AC=BC=3,∠ACB=30°,
12.三棱锥P—ABC的高PO=8,AC=BC=3,∠ACB=30°,
M,N分别在BC和PO上,且CM=x,PN=2CM,试问
下面的四个图象中哪个图象大致描绘了三棱锥N—AMC
|
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分)
|
14.如右图,它满足:(1)第n行首尾两数均为n,
(2)表中的递推关系类似杨辉三角,则第n行
(n≥2)第2个数是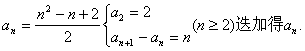
15.国家规定个人稿费纳税办法是:不超过800元的不纳税;超过800 元而不超过4000元的按超过800元部分的14%纳税;超过4000元的按全部稿酬的11%纳税.已知某人出版一本书,共纳税420元时,这个人应得稿费(扣税前)为:
16. 若直线![]() 按向量
按向量![]() 平移后与圆
平移后与圆![]() 相切,则实数
相切,则实数![]() 的值为:
的值为:
三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程,或演算步骤)
17.(本小题满分12分)
已知向量![]() 向量
向量![]() 与向量
与向量![]() 夹角为
夹角为![]() ,且
,且![]() .(1)求向量
.(1)求向量![]() ;
;
(2)若向量![]() 与向量
与向量![]() =(1,0)的夹角为
=(1,0)的夹角为![]() ,其中A,C
,其中A,C
为△ABC的内角,且A,B,C依次成等差数列,试求求![]() +
+![]() 的取值范围.
的取值范围.
18.(本小题满分12分)
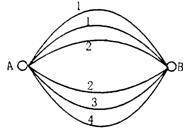
如图,A、B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4.现从中任取三条网线且使每条网线通过最大的信息量.
(I)设选取的三条网线由A到B可通过的信息总量为x,当x≥6时,则保证信息畅通.求线路信息畅通的概率;
|
19.(本小题满分12分)
如图,四棱锥P—ABCD中,底面四边形ABCD是正方形,侧面PDC是边长为a的正
|
(I)求异面直线PA与DE所成的角;
(II)求点D到面PAB的距离.
20.(本小题满分12分)
已知定点![]()
(Ⅰ)求动点P的轨迹方程,并说明方程表示的曲线;
(Ⅱ)当![]() 的最大值和最小值.
的最大值和最小值.
21.(本小题满分14分)
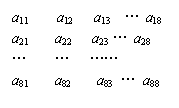 已知64个正整数排成如图所示的8行8列,在符号
已知64个正整数排成如图所示的8行8列,在符号![]() 中,
中,![]() 表示该数所在行数,
表示该数所在行数,![]() 表示该数所在列数.已知每一行的数成等差数列,每一列的数成等比数列,并且所有公比都等于
表示该数所在列数.已知每一行的数成等差数列,每一列的数成等比数列,并且所有公比都等于![]() .若
.若![]()
(1)求![]() 的通项公式;
的通项公式;
(2)记第![]() 行各项和为
行各项和为![]() ,求
,求![]() 的值及数列{
的值及数列{![]() }的通项公式;
}的通项公式;
(3)若![]() <1,求
<1,求![]() 的值.
的值.
22.(本小题满分14分) 已知函数![]() 为实数),
为实数),![]()
![]()
(1)若f (-1) = 0,且函数![]() 的值域为
的值域为![]() ,求
,求![]() 表达式;
表达式;
(2)在(1)的条件下,当![]() 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;
(3)设![]() 为偶函数,判断
为偶函数,判断![]() 能否大于0.
能否大于0.