高考数学普通高等学校招生全国统一考试8
本试卷共22道题，满分150分。考试时间120分钟。
第Ⅰ卷 （共110分）
一、填空题（本大题满分48分）本大题共有12题，只要求直接填写结果，每个空格填对得
4分，否则一律得零分。
1．函数
的最小正周期T=
.
2．若
.
3．在等差数列
中，a5=3,
a6=－2,则a4+a5+…+a10=
.
4．在极坐标系中，定点A
点B在直线
上运动，当线段AB最短
时，点B的极坐标是 .
5．在正四棱锥P—ABCD中，若侧面与底面所成二面角的大小为60°，则异面直线PA与BC所成角的大小等于 .（结果用反三角函数值表示）
6．设集合A={xx<4},B={xx2－4x+3>0}, 则集合{xx∈A且
=
.
7．在△ABC中，sinA;sinB:sinC=2:3:4,则∠ABC= .（结果用反三角函数值表示）
8．若首项为a1，公比为q的等比数列的前n项和总小于这个数列的各项和，则首项a1，公比q的一组取值可以是（a1，q）=
.
9．某国际科研合作项目成员由11个美国人、4个法国人和5个中国人组成.现从中随机选出两位作为成果发布人，则此两人不属于同一个国家的概率为 .（结果用分数表示）
10．方程x3+lgx=18的根x≈ .（结果精确到0.1）
11．已知点
其中n的为正整数.设Sn表示△ABC外接圆的面积，则
=
.
12．给出问题：F1、F2是双曲线
=1的焦点，点P在双曲线上.若点P到焦点F1的距离等于9，求点P到焦点F2的距离.某学生的解答如下：双曲线的实轴长为8，由
PF1－PF2=8，即9－PF2=8，得PF2=1或17.
该学生的解答是否正确？若正确，请将他的解题依据填在下面空格内，若不正确，将正确的结果填在下面空格内.
二、选择题（本大题满分16分）本大题共4题，每题都给出代号为A、B、C、D的四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分.
13．下列函数中，既为偶函数又在（0，π）上单调递增的是 （ ）
A．y=tgx. B．y=cos(－x).
C．
D．
.
14．在下列条件中，可判断平面α与β平行的是 （ ）
A．α、β都垂直于平面r.
B．α内存在不共线的三点到β的距离相等.
C．l，m是α内两条直线，且l∥β，m∥β.
D．l，m是两条异面直线，且l∥α，m∥α, l∥β，m∥β.
15．a1、b1、c1、a2、b2、c2均为非零实数，不等式a1x2+b1x+c1>0和a2x2+b2x+c2>0的解集分别为集合M和N，那么“
”是“M=N”的 （ ）
A．充分非必要条件. B．必要非充分条件.
C．充要条件 D．既非充分又非必要条件.
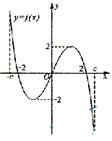
16．f(
)是定义在区间[－c,c]上的奇函数，其图象如图所示：令g（）=af（）+b，则下
|
）的叙述正确的是 （ ）
A．若a<0,则函数g（）的图象关于原点对称.
B．若a=－1，－2<b<0,则方程g（）=0有大于2的实根.
C．若a≠0,b=2,则方程g（）=0有两个实根.
D．若a≥1,b<2,则方程g（）=0有三个实根.
三、解答题（本大题满分86分）本大题共有6题，解答下列各题必须写出必要的步骤.
17．（本题满分12分）
已知复数z1=cosθ－i，z2=sinθ+i，求 z1·z2的最大值和最小值.
18．（本题满分12分）
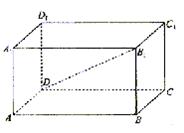
已知平行六面体ABCD—A1B1C1D1中，A1A⊥平面ABCD，AB=4，AD=2.若B1D⊥BC，直线B1D与平面ABCD所成的角等于30°，求平行六面体ABCD—A1B1C1D1的体积.
|
19．（本题满分14分）本题共有2个小题，第1小题满分5分，第2小题满分9分.
已知数列（n为正整数）是首项是a1，公比为q的等比数列.
（1）求和：
（2）由（1）的结果归纳概括出关于正整数n的一个结论，并加以证明.
20．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.
|
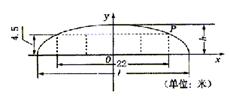
（1）若最大拱高h为6米，则隧道设计的拱
宽l是多少？
（2）若最大拱高h不小于6米，则应如何设
计拱高h和拱宽l，才能使半个椭圆形隧
道的土方工程量最最小？
（半个椭圆的面积公式为
，柱体体积为：底面积乘以高.本题结果精确到0.1米）
21．（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分5分，第3小题满分7分.
在以O为原点的直角坐标系中，点A（4，－3）为△OAB的直角顶点.已知AB=2OA，且点B的纵坐标大于零.
（1）求向量
的坐标；
（2）求圆
关于直线OB对称的圆的方程；
（3）是否存在实数a，使抛物线
上总有关于直线OB对称的两个点？若不存在，说明理由：若存在，求a的取值范围.
22．（本题满分18分）本题共有3个小题，第1小题满分5分，第2小题满分6分，第3小题满分7分.
已知集合M是满足下列性质的函数f(x)的全体：存在非零常数T，对任意x∈R，有f(x+T)=T f(x)成立.
（1）函数f(x)= x 是否属于集合M？说明理由；
（2）设函数f(x)=ax（a>0,且a≠1）的图象与y=x的图象有公共点，证明：
f(x)=ax∈M；
（3）若函数f(x)=sinkx∈M ,求实数k的取值范围.
普通高等学校招生全国统一考试（上海卷）
数学（理工农医类）答案
一、（第1题至第12题）
1．π. 2．
. 3．－49 . 4．
. 5．arctg2. 6．[1,3].
7．
8．
的一组数）. 9．
10．2.6 . 11．4π 12．PF2=17.
二、（第13题至第16题）
| 题 号 | 13 | 14 | 15 | 16 |
| 代 号 | C | D | D | B |
三、（第17题至第22题）
17．[解]
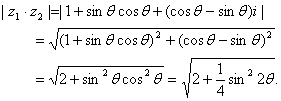
故
的最大值为
最小值为
.
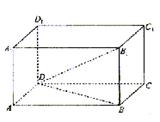
18．[解]连结BD，因为B1B⊥平面ABCD，B1D⊥BC，所以BC⊥BD.
|
.
又因为直线B1D与平面ABCD所成的角等于30°，所以
∠B1DB=30°，于是BB1=
BD=2.
故平行六面体ABCD—A1B1C1D1的体积为SABCD·BB1=
.
19．[解]（1）
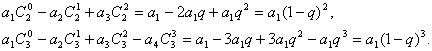
（2）归纳概括的结论为：
若数列是首项为a1，公比为q的等比数列，则
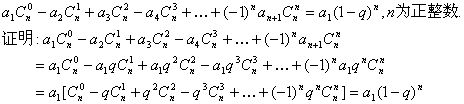
20．[解]（1）如图建立直角坐标系，则点P（11，4.5）， 椭圆方程为
.
|
.因此隧道的拱宽约为33.3米.
（2）[解一]
由椭圆方程，得
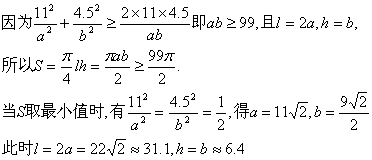
故当拱高约为6.4米、拱宽约为31.1米时，土方工程量最小.
[解二]由椭圆方程，得 于是
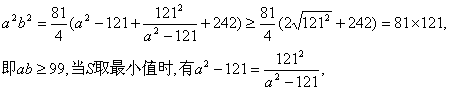
得
以下同解一.
21．[解]（1）设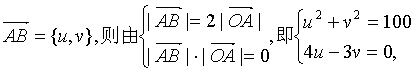
得
所以v－3>0,得v=8,故={6，8}.
（2）由
={10，5}，得B（10，5），于是直线OB方程：
由条件可知圆的标准方程为：(x－3)2+y(y+1)2=10,
得圆心（3，－1），半径为
.
设圆心（3，－1）关于直线OB的对称点为（x ,y）则
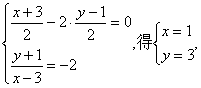故所求圆的方程为(x－1)2+(y－3)2=10.
（3）设P (x1,y1), Q (x2,y2) 为抛物线上关于直线OB对称两点，则
故当
时，抛物线y=ax2－1上总有关于直线OB对称的两点.
22．[解]（1）对于非零常数T，f(x+T)=x+T,
Tf(x)=Tx. 因为对任意x∈R，x+T=
Tx不能恒成立，所以f(x)=
（2）因为函数f(x)=ax（a>0且a≠1）的图象与函数y=x的图象有公共点，
所以方程组：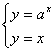
有解，消去y得ax=x,
显然x=0不是方程ax=x的解，所以存在非零常数T，使aT=T.
于是对于f(x)=ax有
故f(x)=ax∈M.
（3）当k=0时，f(x)=0，显然f(x)=0∈M.
当k≠0时，因为f(x)=sinkx∈M，所以存在非零常数T，对任意x∈R，有
f(x+T)=T f(x)成立，即sin(kx+kT)=Tsinkx .
因为k≠0，且x∈R，所以kx∈R，kx+kT∈R，
于是sinkx ∈[－1，1]，sin(kx+kT) ∈[－1，1]，
故要使sin(kx+kT)=Tsinkx .成立，
只有T=
，当T=1时，sin(kx+k)=sinkx
成立，则k=2mπ, m∈Z .
当T=－1时，sin(kx－k)=－sinkx 成立，
即sin(kx－k+π)= sinkx 成立，
则－k+π=2mπ, m∈Z ，即k=－2(m－1) π, m∈Z .
综合得，实数k的取值范围是{kk= mπ, m∈Z}