高考数学模拟试题二答案

高考数学模拟试题二NJGZ

一、选择题（本大题共12小题，每小题5分，共60分.在每小题的四个选项中，只有一项是符合题目要求的）

1.已知直线l、m，平面α、β，且l⊥α,mβ.给出下列四个命题：（1）若α∥β,则l⊥m;(2)若l⊥m,则α∥β;(3)若α⊥β,则l∥m;(4)若l∥m,则α⊥β

其中正确的命题个数是(D)

A.4　　　　　 　　 B.1　　　　　　　　 C.3　 　　　　　　D.2

2.已知数列｛a_n｝的前n项和S_n=aⁿ－1(a∈R,a≠0),则｛a_n｝(C)

A.一定是等差数列　　　　　　　　　　  B.一定是等比数列

C.或者是等差数列，或者是等比数列　　　D.等差、等比数列都不是

3.函数y=1+3x－x³有(D)

A.极小值－1，极大值1　　　　　　　　　B.极小值－2，极大值3

C.极小值－2，极大值2　　　　　　　　  D.极小值－1，极大值3

4.k∈R,直线（k+1）x－ky－1=0被圆（x－1）²+(y－1)²=4截得的弦长是(C)

A.8　　　　　　 B.2　　　　　　 C.4　　　　　　 D.值与k有关

5.异面直线a、b成80°角，P为a、b外一定点，若过P有且仅有2条直线与a、b所成角都为θ，则θ∈(B)

A.｛θ｜0°＜θ＜40°｝　　　　  B.｛θ｜40°＜θ＜50°｝

C.｛θ｜40°＜θ＜90°｝　　　　 D.｛θ｜50°＜θ＜90°｝

6.椭圆=1(a＞b＞0)的四个顶点为A、B、C、D，若菱形ABCD的内切圆恰好过焦点，则椭圆的离心率是(D)

A.　　　 B. 　　　　C. 　　　　 D.

依题意c=即c²(a²+b²)=a²b²又b²=a²－c²故c⁴－3a²c²+a⁴=0

即()⁴－3()²+1=0故e²=()²=(舍正)，e=

7.在椭圆=1上有一点P，F₁、F₂是椭圆的左右焦点，△F₁PF₂为直角三角形，则这样的点P有(D)

A.2个　　　　　　　　　　　　　B.4个　　　　　　　　　　　　　C.6个　　　　　　　　　　　　　D.8个

8.抛物线的焦点是（2，1），准线方程是x+y+1=0，则抛物线的顶点是(B)

A.（0，0）　　　　　　　　　B.（1，0）　　　　　　　　　　　　 C.(0, －1)　　　　　　　　　　　　　 D.(1,1)

9.函数y=f(x)和函数y=g(x)的图象如下图所示，则y=f(x)·g(x)的图象可能是(A)

 

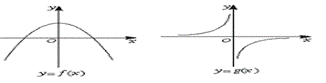
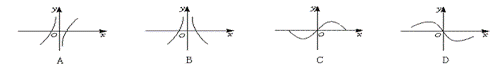
10.把长12厘米的细铁丝截成两段，各自围成一个正三角形，那么这两个正三角形面积之和的最小值是（D）

A. cm² B.4 cm²　　　　 C.3 cm²D.2 cm²

11.学校要从4名爱好摄影的同学中选派3名分别参加校外摄影小组的3期培养（每期只派1名），由于时间上的冲突，甲、乙两人都不能参加第1期培训，则不同的选派方式有(C)

A.6种　　　　　　　　　　　　　　　　 B.8种　　　　　　　　　　　　　C.12种　　　　　　　　 D.16种

12.△ABC中，AB=9，AC=15，∠BAC=120°，△ABC所在平面外一点P到三个顶点A、B、C的距离都是14，那么点P到平面α的距离为(A)

A.7　　　　　　　　　　　　　　　　　　 B.9　　　　　　　　　　　　　　　C.11　　　　　　　　　　　D.13

二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）

13.设f(x)=x²+x+的定义域是［n,n+1］（n∈N^*）,则函数f(x)的值域中含有的整数的个数为2n+2.

14.若抛物线上的各点与焦点距离最小值是2，则过焦点与抛物线的对称轴成角的弦长是

15.已知函数f(x)满足：f(p+q)=f(p)f(q),f(1)=3,则

=_______________.

.解：观察得和式通项为.由已知

令p=q=n得f²(n)=2n又f(2n)=f［(2n－1)+1］=f(2n－1)f(1),及f(1)=3,

故f(2n)=3f(2n－1),故通项为=2×3=6,原式=4×6=24.

16．为顶点的与圆(r>0)没有公共点，则

圆的半径r的取值范围：

三、解答题（本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤）

17.（本小题满分12分）

甲、乙两个乒乓球运动员进行乒乓球单打比赛，已知在一局比赛中甲获胜的概率为0.6，乙获胜的概率为0.4，比赛时可以用三局两胜或五局三胜制，问在哪一种比赛制度下甲获胜的可能性较大？

①如果采用三局二胜制，则甲在下列两种情况下获胜：A－2∶0（甲净胜两局）；A₂－2∶1(前两局各胜一局，第三局甲胜).

P(A₁)=P₂(0)=·0.6²×0.4⁰=0.36,P(A₂)=P₂(1)×0.6=·0.6×0.4×0.6=0.288.

因A₁，A₂互斥，故甲获胜的概率为P（A₁+A₂）=P（A₁）+P（A₂）=0.648.

②如果采用五局三胜制，则甲在下列三种情况下获胜：B₁－3∶0（甲净胜三局）

B₂－3∶1（前三局中甲胜两局，负一局，第四局甲胜）；

B₃－3∶2（前四局中甲、乙各胜两局，第五局甲胜）；同①可求甲获胜的概率为0.682.

由①②的结果知，甲在五局三胜制中获胜的可能性更大.

18.如图，四棱锥P—ABCD中，PD⊥平面ABCD，PA与平面

ABCD所成的角为60°,在四边形ABCD中，∠D=∠DAB=90°，

AB=4，CD=1，AD=2.

　　　 （Ⅰ）建立适当的坐标系，并写出点B、P的坐标；

　　　 （Ⅱ）求异面直线PA与BC所成的角；

　　　 （Ⅲ）若PA的中点为M，求证：平面AMC⊥平面PBC.

解（Ⅰ）建立如图所示的空间直角坐标系

　　　　　 ∵∠D=∠DAB=90°，AB=4，CD=1，AD=2，

　　　　　 ∴A（2，0，0），C（0，1，0），B（2，4，0）.

　　　　　 由PD⊥平面ABCD，得∠PAD为PA与平面ABCD所成的角，∴∠PAD=60°.

　　　　　 在Rt△PAD中，由AD=2，得PD=，

　　　　　 ∴.

　　　　　 （Ⅱ）

　　　　　

　　　　　 所以PA与BC所成的角为

　　　　　 （Ⅲ）.

　　　　　  

　　　　　 ，

　　　　　  

　　　　　

　　　 .

19.（本小题满分12分）

 市场营销人员对过去几年某产品的价格及销售数量的关系做数据分析，有如下的规律，该商品的价格每上涨x%(x＞0),销售量就减少kx%（其中k为正常数），目前该商品定价为a元，统计其销售量为b个.

（1）当k=时，该商品的价格上涨多少，就能使销售的总金额达到最大？

（2）在适当的涨价过程中，求使销售总金额不断增加时，k的取值范围.

解：设销售总额为y,由已知条件知y=a(1+x%)·b(1-kx%)=ab(1+x%)(1-kx%)

(1)当k=时，y=ab(1+)(1-)= (100+x)(200-x)

= (-x²+100x+20000)

x=50时，y_max=ab，即在价格上涨50%时，销售总额最大值为ab.

(2)y=［-kx²+100(1-k)x+10000］定义域为(0,)

由题设知函数y在（0，）内是单调递增函数∴＞0,0＜k＜1

20.（本小题满分12分）

直线l：y=mx+1与椭圆C：ax²+y²=2交于A、B两点，以OA、OB为邻边作平行四边形OAPB（O为坐标原点）

（1）当a=2时，求点P的轨迹方程；

（2）当a,m满足a+2m²=1，且记平行四边形OAPB的面积函数S（a）,求证：2＜S(a)＜4.

（1）解：设P（x,y），则OP中点为E（）

由消去y得（2+m²）x²+2mx-1=0设A(x₁,y₁),B(x₂,y₂)

则=－,=m+1=

即AB的中点为E（－,）

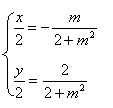于是

消去m,得点P的轨迹方程为2x²+y²-2y=0

 (2)证明：由消去y得(a+m²)x²+2mx-1=0进一步就可以求出AB=

∵O到AB的距离d=·S(a)=ABd=

∵a+2m²=1∴0＜a＜1∴2＜S(a)＜4

21.（本小题满分12分）

设f(x)=ax²+bx+c(a＞b＞c),f(1)=0,g(x)=ax+b.

（1）求证：函数y=f(x)与y=g(x)的图象有两个交点；

（2）设f(x)与g(x)的图象交点A、B在x轴上的射影为A₁、B₁，求｜A₁B₁｜的取值范围；

（3）求证：当x≤－时，恒有f(x)＞g(x).

（1）证明： 　　　y=f(x)=ax²+bx+c

　　　　　　　　  y=g(x)=ax+b　得ax²+(b－a)x+(c－b)=0　

Δ=(b－a)²－4a(c－b)∵f(x)=ax²+bx+c,f(1)=0　

∴f(1)=a+b+c=0又a＞b＞c　∴3a＞a+b+c＞3c即a＞0,c＜0

∴b－a＜0,c－b＜0,a＞0∴Δ=(b－a)²－4a(c－b)＞0

故函数y=f(x)与y=g(x)的图象有两个交点；

（2）解：设A、B的坐标分别为（x₁,y₁）、（x₂，y₂），

则x₁、x₂是方程（*）的两根故x₁+x₂=－,

x₁x₂=,所以｜A₁B₁｜=｜x₁－x₂｜=

==又a+b+c=0,故b=－(a+c)

因而(b－a)²－4a(c－b)=(－2a－c)²－4a(a+2c)=c²－4ac

故｜A₁B₁｜===

∵a＞b＞c,a+b+c=0∴a＞－(a+c)＞c　

∴－2＜＜－∴｜A₁B₁｜的取值范围是（，2）.

(3)证明：不妨设x₁＞x₂,则由（2）知：

＜x₁－x₂＜2　x₁+x₂=－=1－由a＞b＞c得：＜＜1,

故0＜1－＜1－ 又－2＜＜－,故＜1－＜3,

因而0＜1－≤即0＜x₁－x₂≤ 由①、②得：－＜x₂≤0,

即方程（*），也就是方程f(x)－g(x)=0的较小根的范围是（－，0].

又a＞0,故当x≤－时，f(x)－g(x)＞0恒成立，即当x≤－时，恒有f(x)＞g(x).

22.（本小题满分12分）

已知函数f(x－2)=ax²－(a－3)x+a－2(a＜0,a∈Z)的图象与x轴有交点.

（1）求a的值；（2）求f(x)的解析式；

（3）若g(x)=1－［f(x)］²,F(x)=c·g(x)+d·f(x)，问是否存在c(c＞0)，d使得在区间（-∞,f(2)）内是单调递增函数，而在区间（f(2),0)内是单调递减函数？若存在，求c,d之间的关系，并写出推理过程；若不存在，说明理由.

解：

（1）a=－1;

(2)f(x)=－x²+1

(3)g(x)=－x⁴+2x²,F(x)=－cx⁴+(2c－d)x²+d(c＞0).

若F(x)在（－∞,f(2)）,即在（－∞，－3）上为增函数，则当x₁＜x₂＜－3时F（x₂)－F(x₁)＞0,于是有（x₂²－x₁²)［－c(x₁²+x₂²)+2c－d］＞0.

∵x₂²－x₁²＜0,∴－c(x₁²+x₂²)+2c－d＜0.

∴x₁²+x₂²＞.

要使该式在（－∞,3）上恒成立，只须≤(－3)²+(－3)²=18,即16c+d≥0,同样的方法可得，要使F(x)在（－3，0）上为减函数，只须16c+d≤0,因此当16c+d=0时满足给出的所有条件.

另解：依题意，F（x)在x=－3时有极大值，

∵F′(x)=－4cx³+2(2c－d)x,

∴F′(x)_x=－3=0,同样可得16c+d=0.