高考数学模拟试题七NJGZ
第I卷（选择题，共60分）
一、选择题（本大题共12个小题，每小题5分；共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．
的值为 （B）
A．1 B．i C．－i D．－1
2．设函数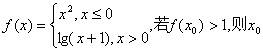
的取值范围为 （D）
A．（－1，1） B．（－1，+∞） C．
D．
3．若过球面上A、B、C三点的截面与球心的距离恰为球半径的一半，且AB=BC=CA=2，
则球体积为 （D）
A．
B．
C．
D．
4．椭圆
的焦点为F1和F2，点P在椭圆上，若线段PF1的中点在y轴上，那么
PF1 : PF2的值为 （B）
A．
B．
C．
D．
5．已知A、B、C、D是坐标平面上不共线的四点，则
共线是
=0
的什么条件 （B）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
6．设函数
的图象关于直线
对称，它的周期是
，则 （C）
A．
B．
C．
D．
7．O是平面上一定点，A、B、C是平面上不共线的三点，动点P满足
，则P的轨迹一定通过△ABC的 （C）
A．外心 B．重心 C．内心 D．垂心
8．设f (x)是一个元三次函数
等于 （A）
A．2 B．
C．
D．4
9．对于任意
的值恒大于零，那么x的取值范围是 （B）
A．（1，3） B．
C．（1，2） D．
10．过圆锥曲线C的一个焦点F的直线l交C于A、B，且以AB为直径的圆与F相对应的准线相交，则曲线C是 （B）
A．椭圆 B．双曲线 C．抛物线 D．以上都有可
11．等边△ABC的边长为a，将它沿平行于BC的线段PQ折起，使平面APQ⊥平面BPQC，若折叠后AB的长为d，则d的最小值是 （D）
A．
B．
C．
D．
12．函数
，给出下述命题：
①
有最小值； ②当
的值域为R；
③当
上有反函数，则其中正确的命题是 （B）
A．①②③ B．②③ C．①② D．①③
第Ⅱ卷（非选择题，共90分）
二、填空题（本大题共4个小题，每小题4分，共16分，将答案填在题中的横线上.）
13．已知曲线
则在曲线上:（4，5）点处的切线与直线
垂直.
14．已知F1、F2是椭圆C的两个焦点，P为C上一点，且P到一条准线的距离是PF1、PF2的等差中项，则C的离心率的取值范围是: 
.
15．关于
:
.
16．如图，一条直角走廊宽为1.5m，一转动灵活的平板手推车，其平板面为矩形，宽
为1m.问：要想顺利通过直角走廊，平板手推车的长度不能超过：
米.
三、解答题（本大题共6个小题，共74分，解答要写出文字说明、证明过程或解题步骤）
17．（本小题满分12分）
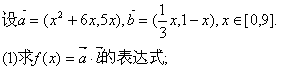
(2)求
的单调增区间；(3)求的最大值和最小值.
解：（1）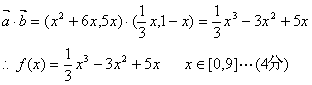
（2）
18．（本小题满分10分）
甲、乙两名篮球运动员，各自的投篮命中率分别为0.7与0.8，如果每人投篮两次.
（1）求甲比乙多投进一次的概率；
（2）若投进一个球得2分，未投进得0分，求两人得分之和的期望值.
解：（1）设甲进一球，乙一球没进为事件A
甲进两球，乙进一球设为事件B
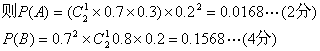
所以甲比乙多进一球的概率
P=P（A+B）=P（A）+P（B）=0.1736……（6分）
（2）设ξ表示两人投球后的得分和
| ξ | 0 | 2 | 4 | 6 | 8 |
| P | 0.0036 | 0.0456 | 0.2116 | 0.4256 | 0.3136 |
……（10分）
……（12分）
19．（本小题满分12分）如图，正四棱锥P—ABCD中，AB=2，侧棱PA与底面ABCD所成的角为60°。（1）求侧面与底面所成的二面角（锐角）的大小；
（2）在线段PB上是否存在一点E，使得AE⊥PC，若存在，试确定点E的位置，并加以证明，若不存在，请说明理由.
解：（1）如图O为底面ABCD的中心
则∠PAO为PA与底面所成的角
∴∠PAO=60°
∵
∴
……（2分）
过O作OM⊥BC于M，连PM由三垂线定理得BC⊥PM
∴∠PMO为侧面与底面所成二面角平面角……（4分）
∵OM=1，PO=
……6分
（2）如图建立空间直角坐标系
20．（本小题满分12分）
已知数列
总成等差数列.
（1）求a2，a3，a4的值；（2）求通项an；（3）计算
解：（1）由题意知
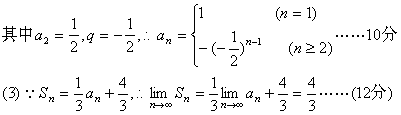
21．（本小题满分12分）
已知奇函数
又有函数
（1）求
（2）求
解：（1）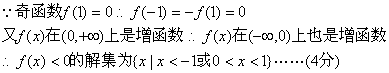
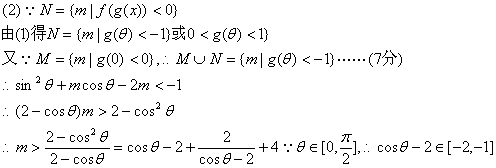
22．（本小题满分14分）
已知曲线
（1）求：当k=1时C′的方程;
（2）求证：对任意实数k，C与C′恒有公共点.
解：（1）设点P′(x,y)为C′上任一点，则P′关于l的对称点P(x0,y0)在C上…（1分）
（2）当l与C有公共点或C上有两不同点关于l对称时，C与C′有交点，当l与C有公共点时
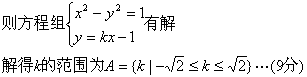
当C上存在两不同点
则lAB与C有交点且中点M在l上
