高三联考数学试卷1

高三联考数学试卷1

本试卷分第I卷（选择题）和第II卷（非选择题）两部分。共150分。考试时间120分钟。

第I卷（选择题　　　　共60分）

参考公式：

如果事件A、B互斥，那么P（A+B）=P（A）+P（B）

如果事件A、B互相独立，那么P（A·B）=P（A）·P（B）

如果事件A在一次试验中发生的概率是P，那么它在n次独立重复试验中恰好发生k次的概率

P（k）=CP（1－P）

正棱锥、圆锥的侧面积公式S=cl　其中c表示底面周长，l表示斜高或母线长

球的体积公式V=　其中R表示球的半径

一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题

目要求的。

1．　设I={1，2，3，4}，A与B是I的子集，若AB={1，3}，则称（A、B）为一个“理想配集”。那么符合此条件的“理想配集”的个数是（规定（A、B）与（B、A）是两个不同的“理想配集”）

　　　 A．4　　　　　　　　　　　　　　B．8　　　　　　　　　　　　　　C．9　　　　　　　　　　　　　　D．16

2．　函数y =sin x+cos x，x[－]的值域是

　　　 A．[－，3]　　　　　　B．[－2，2]　　　　　　　　 C．[0，2]　　　　　　　　　　D．[0，]

3．　  已知向量a =（2，3），b =（－1，2），若ma+b与b－2b平行，则m等于

A．－2　　　　　　　　　　　　B．2　　　　　　　　　　　　　　C．－　　　　　　　　　　　D．

4．　  a =－1是直线ax+（2a－1）y+1=0和直线3x+ay+3=0垂直的

A．充分不必要条件　　　　　　　　　　　　　B．必要不充分条件

C．充要条件　　　　　　　 　　　　　　　　　　 D．既不充分又不必要条件

5．　  已知直线a、b与平面，给出下列四个命题

①若a//b，b，则a//　　　　　 ②若a//，b，则a//b；

③若a//，b//，则a//b　　　 ④a，b//，则ab。

其中正确的命题是

A．①和②　　　　　 B．①和④　　　　　 C．③和④　　　　　 D．只有④

6．　  某池塘有A、B、C三只小船，A船可坐3人，B船可坐2人，C船可坐1人。今有2个成人和2个儿

童分乘这些船只，为安全起见，儿童必须由成人陪同才能乘船，他们分乘这些船只的方法共有

A．12种　　　　　　　　　　　B．8种　　　　　　　　　　　　C．7种　　　　　　　　　　　 D．2种

7．　  设a、b、u都是正实数，且a、b满足，则使得a+bu恒成立的u范围是

A．（0，16）　　　　　　　 B．（0，12）　　　　　　　　C．（0，10）　　　　　　　 D．（0，8）

8．　　在研究复数性质时，规定：如果对n个复数a，a，a，…，a，存在不全为零的n个实数k，k，k，…，k，使得ka+ ka+ ka+…+ ka=0成立，那么叫做“线性相关”。依此规定，能使a=1，a=1－i，a=2+2i“线性相关”的实数k，k，k可以取

A．k=1，k=2， k=3　　　　　　　　　B．k=－4， k=2， k=1

C．k=－1，k=0，k=1　　　　　　　　D．k=0，k=0，k=0

9．　  已知{ a}的前n项和S=n－4n+1，则 a + a+…+ a=

A．68　　　　　　　　　 B．67　　　　　　　　　 C．61　　　　　　　　　 D．60

10．若双曲线x－y=1的左支上一点P（a，b）到直线y = x的距离为，则a+b的值为

A．－　　　　　　　 B．　　　　　　　　　 C．－2　　　　　　　　 D．2

11．用记号“”表示求两个实数a与b的算术平均数的运算，即ab=。已知数列{x}满足x=0,

　　　 x=1，x=xx（n），则lim　x等于

　　　 A．0　　　　　　　　　　　　　　B．　　　　　　　　　 C．　　　　　　　　　D．1

12．某债券市场常年发行三种债券，A种面值1000元，一年到期本息和为1040元；B种贴水债券面值为

1000元，但买入价为960元，一年到期本息和为1000元；C种面值为1000元，半年到期本息和为1020元。设这三种债券的年收益率分别为a、b、c，则a、b、c的大小关系是

A．a = c且a<b　　　　　　B．a<b<c　　　　　　　C．a<c<b　　　　　　 D．c<a<b

第II卷（非选择题　共90分）

二、填空题：本大题共4小题，每小题4分，共16分。把答案直接填在题中横线上。

13．函数y = x+sincos的导数是　　　　　　　  。

14．袋中有些大小相同的小球，其中号数为1的小球1个，号数为2的小球2个，号数为3的小球3个，

　　　 …，号数为n的小球n个，从袋中取一球，其号数记为随机变量，则的数学期望E=　　　　。

15．三棱台ABC—ABC上、下底面面积分别为S、S（S>S），棱BC与截面ABC的距离等于这个棱台的高，则ABC的面积等于　　　　　　　　  。

16．已知OFQ的面积为S，且·=1。若<S<2，则向量与的夹角的取

　　　 值范围是　　　　　　　　　　  。

三、解答题：本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。

17．（本小题满分12分）

已知：定义在区间[－，]上的函数y = f（x）的图象关于直线x =对称，当x时，函数f（x）=sin x 。

（1）　　　 求f（－），f（－）的值；

（2）　　　 求y = f（x）的函数表达式；

（3）　　　 如果关于x的方程f（x）= a有解，那么将方程在a取某一确定值时所求得的所有解的和记为M。求M的所有可能取值及相对应的a的取值范围。

18．（本小题满分12分）

如图：用A、B、C、D四类不同的元件连接成系统N，当元件A正常工作且元件B、C都正常工作或当元件A正常工作且元件D正常工作时，系统N正常工作。已知元件A、B、C、D正常工作的概率依次为、、、。

（1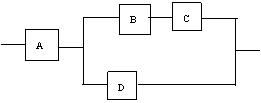）　　　 求元件A不正常工作的概率；

（2）　　　 求元件A、B、C都正常工作的概率；

（3）　　　 求系统N正常工作的概率。

19．（本小题满分12分）

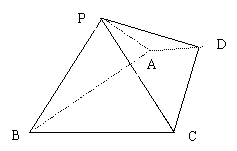　　　 如图：已知四棱锥P—ABCD的底面为直角梯形，AD//BC，BCD=90，

PA=PB，PC=PD。

（1）　　　 证明CD与平面PAD不垂直；

（2）　　　 证明平面PAB平面ABCD；

（3）　　　 如果CD=AD+BC，二面角P－BC－A等于60，求二面角P－CD－A的大小。

20．（本小题满分12分）

　　　 已知函数f（x）=－x+ax在区间（0，1）上是单调递增函数。

（1）　　　 求实数a的取值范围；

（2）　　　 当a取最小值时，定义数列{a}：a=b，a= f（a），若b（0，1），求证a（0，1）。

21．（本小题满分12分）

某城市为了改善交通状况，需进行网络改造。已知原有道路a个标段（注：1个标段是指一个定长度的机动车道），拟增建x个标段的新路口和n个道路交叉口，n与x满足关系n = ax+b，其中b为常数。设新建1个标段道路的平均造价为k万元，新建1个道路交叉口的平均造价是新建1个标段道路的平均造价的倍（1），n越大，路网越通畅，设路网的堵塞率为，它与的关系为=。

（1）　　　 写出新建道路交叉口的总造价y（万元）与x的函数关系式；

（2）　　　 若要求路网的堵塞率介于5％与10％之间，而且新增道路标段为原有道路标段数的25％，求新建的x个标段的总造价与新建道路交叉口的总造价之比P的取值范围；

（3）　　　 当b =4时，在（2）的假设下，要使路网最通畅，且总造价比P最高，问原有道路标段为多少个？

22．（本小题满分14分）

如图，设曲线C：y=x（y0）上的点P的坐标为（x，y），过P做斜率为的直线，与y轴交于Q，过Q点做平行于x轴的直线与曲线C交于P（x，y），然后再过P做斜率为的直线交y轴于Q，过Q点做平行于x轴的直线与曲线C交于P（x，y），仿此，做出如下点列：

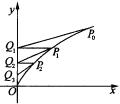P，Q，P，Q，P，Q，…，P，Q，…。已知x=1，设P（x，y）。

（1）　　　 设x=f（n）（n = 0，1，2…），求f（n）的表达式；

（2）　　　 计算：SPQP+SPQP+…+SPQP+… ；

（3）　　　 求 lim  。

高三联考答案

1．  D

2．  D　y=2sin（x+30）

3．  C　xy－xy=0

4．  A

5．  D

6．  B

7．  A

8． 

n=1 n

B

9．  B　a=S=－2，又a=S－S，（n2）， a=2n－5， a=

10．A　设a=sec，b=tan，d==sin=－，cos=－.

11．C　　 x+x= x+x=…=1+×0　lim（x+x）=1lim x=

12．C　　 a=，b=，c=（1+2℅）－1

13．1+cos x

14．（2n+1）/3

15．

16．（，arctan4）　 S= OF · FQ sin〈·〉　

　　　·= · 　cos〈·〉　 S=tan〈·〉

　　　 <S<2， 1< tan〈·〉<4　 又[0，]　 （，arctan4）

17．（1）f（－）= f（）=sin=0，f（－）= f（）=sin=

（2）当－x<时，f（x）= f（－x）=sin（－x）=cos x　 f（x）=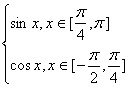

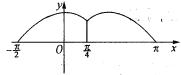（3）做函数f（x）的图象

显然，若f（x）=a有解，则a[0，1]

①0a<，f（x）=a有两解，M=。

②a=，f（x）=a有三解，M=。

③<a<1，f（x）=a有四解，M=。

④a=1，f（x）=a有两解，M=。

18．（1）元件A正常工作的概率P（A）=，它不正常工作的概率P（）=1－P（A）=。

　  （2）元件A、B、C都正常工作的概率P（A·B·C）=P（A）·P（B）·P（C）=··=。

　　　 　 （3）系统N正常工作可分为A、B、C都正常工作和A、D正常工作但B、C不都正常工作两种情况，

　　　　　　　　　　 前者概率为，后者的概率为P（A··C·D）+P（A·B··D）+P（A···D）

　　　　　　　　　　 =···+···+···=，所以系统N正常工作的概率是+=.

19．（1）若CD平面PAD，则CDPD，由已知PC=PD，得PCD=PDC<90°，这与CDPD矛盾，所以CD与平面QAD不垂直。

（2）取AB、CD的中点E、F，联结PE、PF、EF，由PA=PB，PC=PD，得PEAB，PFCD。EF为直角梯形的中位线，EFCD，又PFEF=F，CD平面PEF，由PE平面PEF，得CDPE，又ABPE且梯形两腰AB、CD必相交，PE平面ABCD，又PE墙面PAB，平面PAB平面ABCD。

～

（3）由（2）及二面角定义可知PFE为二面角P－CD－A的平面角，做EGBC于G，连PG，由三垂线定理得BCPG，故PGE为二面角P－CD－A的平面角，即PGE=60°，由已知，得EF=（AD+BC）=CD，又EG=CF=CD。EF=EG，易证得RtPEF = RtPEG。PFE=PGE=60°，即为所求。

20．（1）x，x（0，1），且x<x，则f（x）－f（x）=－（x－x）（x+ xx+x－a）<0，

　　　　　　　x+ xx+x－a，a> x+ xx+x，而x+ xx+x<（x+x）+（x+x）=（x+x）

　　　　　　　<×2=3，a3。

　　　 （2）当a=3时，a=－a+a。下面用数学归纳法证明：0< a<1。

　　　　　　　 当n=1时，a（0，1）；

　　　　　　　 假设n = k时，a（0，1），则a=a（3－a）>0，f（x）在（0，1）上递增，0< a<1，

　　　　 　a=a+a<－·1+·1=1。0< a<1，即n =k+1时，也成立。a（0，1）。

21．（1）依题意得，新建道路交叉口的总造价（单位：万元）为y=kn=k（ax+b）。

　　　（2）P=。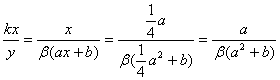

　　　 由于5﹪10﹪，有0.050.1。

　　　 则0.10.2，0.051+10，49，，又由已知P>0，从而>0。

　　　 　　　 P的取值范围是P（无等号不扣分）

　　　（3）当b=4时，在（2）的条件下，若路网最通畅，则=9，又总造价比最高，P=。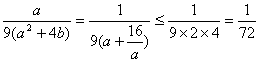

　　　 当且仅当a=时，即a=4时取等号，满足（3）的条件的原有道路路标段是4个

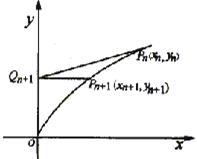22．（1）如图，kQ=，PQ的方程为y－y=（x－x）， y=，y－=（x－x）。令x=0，得y=，又P在y=x

上，y=x，即（）= x=，{ x}是等比数

列，x=f（n）=（）（其中n=0，1，2，…）。

（2）PQP的面积记为S，则S=x（y－y），

而x=（），y==（）， S=（）[（）－（）]=（）。{ S}是首项为S=（）、公比为（）的无穷递缩数列， S+S+S+…+ S+…=

（3） PP==

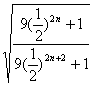（），lim=2 lim=2