 高三联考数学试题
高三联考数学试题
数学试题(文科)
一:选择题:(本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
1. P={1,2,3,4,5},Q={3,4,5,6,7,8},定义P※Q={(a,b)a∈P,b∈Q}
则P※Q中元素的个数为 ( ) 。
(A)4 (B)5 (C)30 (D)120
2.函数![]() , 如果方程
, 如果方程![]() 有且只有一个实根,那么实数
有且只有一个实根,那么实数![]() 应满( ) (A)
应满( ) (A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
3.已知直线y=kx+1与曲线y=x3+ax+b切于点(1,3),则b的值为………( )
(A)3 (B)-3 (C)5 (D)-5
4. 已知i, j为互相垂直的单位向量,a = i – 2j, b =
i + λj,且a与b的夹角为锐角,则实![]() 的取值范围是(
)。
的取值范围是(
)。
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D)
![]()
5. 等比数列{an}中,已知 a1+a2+a3+a4=10, a5+a6+a7+a8=-5,
则数列{an}的前16项和S16为 ( )。.
(A).-50 (B).![]() (C).
(C).![]() (D).-
(D).-![]()
6.宁远一中高三文科一班学生开展研究性学习活动,他们从水市水库中打一网鱼共200kg, 做上记号再放回水库中, 数天后再打一网鱼共有300kg, 其中有5kg有记号, 则能估计水市水库中有鱼 ( )吨。
(A) 12 (B) 10/3 (C) 12/41 (D) 7.5
 7. 设甲、乙两地的距离为a (a>0),小王骑自行车以匀速从甲地到乙地用了20分钟,在乙地休息10分钟后,他又以匀速从乙地返回甲地用了30分钟,则小王从出发到返回原地所经过的路程y和其所用的时间x的函数的图象为 ( )
7. 设甲、乙两地的距离为a (a>0),小王骑自行车以匀速从甲地到乙地用了20分钟,在乙地休息10分钟后,他又以匀速从乙地返回甲地用了30分钟,则小王从出发到返回原地所经过的路程y和其所用的时间x的函数的图象为 ( )
( A ) ( B ) ( C ) ( D ) .
8.已知直线l1的方程为y=x,直线l2的方程为y=ax+b(a,b为实数),当直线l1与l2
夹角的范围为[0,![]()
![]() 时,a的取值范围是 ( )
时,a的取值范围是 ( )
A. (![]() ,1)∪(1,
,1)∪(1,![]() ) B.(
) B.(![]() ,
,![]() )
)
C. (0,1) D.(1,![]() )
)
9.如图①是一个正三棱柱形容器,底面边长为a,高为2a,内装水若干.将容器放倒,把一个侧面作为底面,如图②,这时水面恰好为中截面.请问图①中容器内水面的高度是( )。
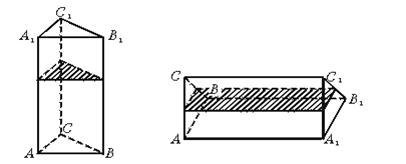
图① 图②
(A) a (B)![]() a (C)
a (C) ![]() a (D)
a (D) ![]() a
a
10. 命题P:如果x2+2x+1-a2<0,那么-1+a<x<-1-a. 命题Q:a<1.那么,
Q是P的 ( )。
(A)必要不充分条件 (B).充分不必要条件
(C 充要条件 (D).既不充分也不必要条件
11.
若f(x)是偶函数,且当x∈[0,+∞![]() 时,f(x)=x-1,则不等式f(x-1)>1的解集是( )
时,f(x)=x-1,则不等式f(x-1)>1的解集是( )
(A).{x-1<x<3} (B).{xx<-1,或x>3}
(C).{xx>2} (D).{xx>3}
![]() 12.将函数y=cos2x的图象F按向量a=(-
12.将函数y=cos2x的图象F按向量a=(-![]() )平移到L,则L的解析式是( )
)平移到L,则L的解析式是( )
A.y=cos(2x+![]() )+
)+![]() B.y=cos(2x-
B.y=cos(2x-![]() )+
)+![]()
C.y=cos(2x+![]() )+
)+![]() D.y=cos(2x-
D.y=cos(2x-![]() )+
)+![]()
(请将选择题的答案填在下面的表內)
![]()
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 |
![]() 二、填空题:(共4小题,每小题4分,共16分.把答案填在题中的横线上).
二、填空题:(共4小题,每小题4分,共16分.把答案填在题中的横线上).
13.已知M为△ABC边AB上一点,且△AMC的面积是△ABC面积的![]() ,则B分
,则B分![]() 所成的比为______.
所成的比为______.
14.甲射击命中目标的概率是![]() ,乙射击命中目标的概率是
,乙射击命中目标的概率是![]() ,丙射击命中目标的概率是
,丙射击命中目标的概率是![]() ,现在三人同时射击目标,则目标被击中的概率为______.
,现在三人同时射击目标,则目标被击中的概率为______.
15.已知数列![]() 满足:
满足:![]() ,则使
,则使![]() 成立的
成立的![]() 的值是 .
的值是 .
16.永州电视台为某个广告公司特约播放赵本山的两个小品。其中小品甲播映时间为20分钟,广告时间为1分钟,收视观众为60万,小品乙播映时间为10分钟,广告时间为1分钟,收视观众为20万。广告公司规定每周至少有6分钟广告,而电视台每周只能为该公司提供不多于86分钟的节目时间。为获得最高的收视率,电视台每周应播映小品甲 次, 小品乙 次。
三、解答题:(本大题共6小题,共74分)
17.(本小题满分12分)
已知函数f(x)=2cos2x+![]() sin2x+a.若x∈[0,
sin2x+a.若x∈[0,![]() ],且f(x)<2,求实数a的取值范围.
],且f(x)<2,求实数a的取值范围.
 18.(本小题满分12分)
18.(本小题满分12分)
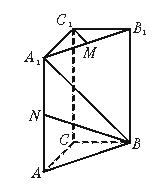
 如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
(1)求BN的长;
(2)求直线BA1与CB1所成角的余弦值
(3)求证:A1B⊥C1M.

![]() 19(本小题满分12分)
19(本小题满分12分)
新田一中高三文科一班学生开展研究性学习活动,他们在学校大门口观察发现:有A、B、C三辆公汽按A、B、C顺序依次连续不断在校门口载客;候车人中大约有三分之一是学生。公汽公司为鼓励学生乘车,每月给第一个乘坐公汽的学生免收一个月的乘车费。你认为乘坐哪一辆公汽最有可能免收一个月的乘车费?并说明理由。
20.(本小题满分12分)
已知![]() ,设
,设 ![]()
![]() ,
,
试寻求使得![]() 都成立的
都成立的![]() 的集合.
的集合.
![]()
![]()
![]()
![]()
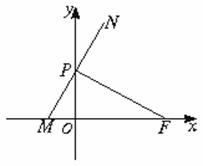
![]() 21.(本小题满分12分)如图,点F(a,0)(a>0),点P在y轴上运动,M在x轴上,N为动点,且
21.(本小题满分12分)如图,点F(a,0)(a>0),点P在y轴上运动,M在x轴上,N为动点,且![]() 0.
0.
(1)求点N的轨迹C的方程;
(2)过点F(a,0)的直线l(不与x轴垂直)与曲线C交于A、B两点,设点
![]()
![]()
 K(-a,0),
K(-a,0),![]() 与
与![]() 的夹角为θ ,
求证0<θ <
的夹角为θ ,
求证0<θ <![]() .
.
22.(本小题满分14分)
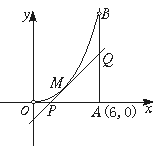 如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于点P,交线段AB于点Q,
如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于点P,交线段AB于点Q,
(1)试用t表示切线PQ的方程;
(2)试用t表示出△QAP的面积g(t);若函数g(t)在(m,n)上单调递减,试求出m的最小值;
(3)若S△QAP∈[![]() ,64],试求出点P横坐标的取值围。 .
,64],试求出点P横坐标的取值围。 .
 高三联考
高三联考
数学试题(文科)及参考答案
一:选择题:(本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
2. P={1,2,3,4,5},Q={3,4,5,6,7,8},定义P※Q={(a,b)a∈P,b∈Q}
则P※Q中元素的个数为 ( ) 。
(A)4 (B)5 (C)30 (D)120
解:5X6=30 选C
2.函数![]() , 如果方程
, 如果方程![]() 有且只有一个实根,那么实数
有且只有一个实根,那么实数![]() 应满( ) (A)
应满( ) (A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
![]()
![]()
![]() 解:选C
解:选C
3.已知直线y=kx+1与曲线y=x3+ax+b切于点(1,3),则b的值为………( )
(A)3 (B)-3 (C)5 (D)-5
![]() 解:把(1,3)代入y=kx+1得k=2 由f /
(1)=2 (3x2+a) x=1=2 3x12+a=2
解:把(1,3)代入y=kx+1得k=2 由f /
(1)=2 (3x2+a) x=1=2 3x12+a=2
a=-1 f(1)=3 1+a+b=3 b=3 故选A
4. 已知i, j为互相垂直的单位向量,a = i – 2j, b =
i + λj,且a与b的夹角为锐角,则实![]() 的取值范围是(
)。
的取值范围是(
)。
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D)
![]()
解:a*b=( i – 2j )*( i + λj ) =i2-2λj2+(λ-2) i*j
=1-2λ>0 λ<1/2 但不等于-2 故选B
5. 等比数列{an}中,已知 a1+a2+a3+a4=10, a5+a6+a7+a8=-5,
则数列{an}的前16项和S16为 ( )。.
(A).-50 (B).![]() (C).
(C).![]() (D).-
(D).-![]()
解:等比数列每连续四项的和也成等比数列,即已知b1=10 q= -1/2
求{bn}的前四项的和T4=?故选B
6.宁远一中高三文科一班学生开展研究性学习活动,他们从水市水库中打一网鱼共200kg, 做上记号再放回水库中, 数天后再打一网鱼共有300kg, 其中有5kg有记号, 则能估计水市水库中有鱼 ( )吨。
(A) 12 (B) 10/3 (C) 12/41 (D) 7.5
解:5:300=200:x 选A
 7. 设甲、乙两地的距离为a (a>0),小王骑自行车以匀速从甲地到乙地用了20分钟,在乙地休息10分钟后,他又以匀速从乙地返回甲地用了30分钟,则小王从出发到返回原地所经过的路程y和其所用的时间x的函数的图象为 ( )
7. 设甲、乙两地的距离为a (a>0),小王骑自行车以匀速从甲地到乙地用了20分钟,在乙地休息10分钟后,他又以匀速从乙地返回甲地用了30分钟,则小王从出发到返回原地所经过的路程y和其所用的时间x的函数的图象为 ( )
( A ) ( B ) ( C ) ( D ) .
解:选D
8.已知直线l1的方程为y=x,直线l2的方程为y=ax+b(a,b为实数),当直线l1与l2
夹角的范围为[0,![]()
![]() 时,a的取值范围是 ( )
时,a的取值范围是 ( )
A. (![]() ,1)∪(1,
,1)∪(1,![]() ) B.(
) B.(![]() ,
,![]() )
)
C. (0,1) D.(1,![]() )
)
解:tan![]() =2-
=2-![]()
![]() 选B
选B
9.如图①是一个正三棱柱形容器,底面边长为a,高为2a,内装水若干.将容器放倒,把一个侧面作为底面,如图②,这时水面恰好为中截面.请问图①中容器内水面的高度是( )。
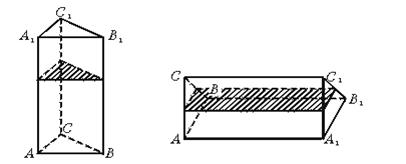
图① 图②
(A) a (B)![]() a (C)
a (C) ![]() a (D)
a (D) ![]() a
a
解:![]() 故选C
故选C
10. 命题P:如果x2+2x+1-a2<0,那么-1+a<x<-1-a. 命题Q:a<1.那么,
Q是P的 ( )。
(A)必要不充分条件 (B).充分不必要条件
(C 充要条件 (D).既不充分也不必要条件
![]() 解:x2+2x+1-a2<0 (x+1)2<a2 与-1+a<x<-1-a.比较知.
解:x2+2x+1-a2<0 (x+1)2<a2 与-1+a<x<-1-a.比较知.
![]()
![]()
![]() 命题P:a≤0 命题Q:a<1 命题Q:a<1 命题P:a≤0
命题P:a≤0 命题Q:a<1 命题Q:a<1 命题P:a≤0
故选A
11.
若f(x)是偶函数,且当x∈[0,+∞![]() 时,f(x)=x-1,则不等式f(x-1)>1的解集是( )
时,f(x)=x-1,则不等式f(x-1)>1的解集是( )
(A).{x-1<x<3} (B).{xx<-1,或x>3}
(C).{xx>2} (D).{xx>3}
![]() 12.将函数y=cos2x的图象F按向量a=(-
12.将函数y=cos2x的图象F按向量a=(-![]() )平移到L,则L的解析式是( )
)平移到L,则L的解析式是( )
A.y=cos(2x+![]() )+
)+![]() B.y=cos(2x-
B.y=cos(2x-![]() )+
)+![]()
C.y=cos(2x+![]() )+
)+![]() D.y=cos(2x-
D.y=cos(2x-![]() )+
)+![]()
![]()
![]() 解:点移加,线移减 y-1/2=cos2[x-(-
解:点移加,线移减 y-1/2=cos2[x-(-![]() )]
y=cos(2x+
)]
y=cos(2x+![]() )+
)+![]()
故选A
(请将选择题的答案填在下面的表內)
![]()
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 | C | C | A | B | B | A | D | B | C | A | B | A |
![]() 二、填空题:(共4小题,每小题4分,共16分.把答案填在题中的横线上).
二、填空题:(共4小题,每小题4分,共16分.把答案填在题中的横线上).
13.已知M为△ABC边AB上一点,且△AMC的面积是△ABC面积的![]() ,则B分
,则B分![]() 所成的比为______ -
8/7 C
所成的比为______ -
8/7 C
![]()
![]()
![]() A 1 M 7 B
A 1 M 7 B
14.甲射击命中目标的概率是![]() ,乙射击命中目标的概率是
,乙射击命中目标的概率是![]() ,丙射击命中目标的概率是
,丙射击命中目标的概率是![]() ,现在三人同时射击目标,则目标被击中的概率为______. 0.75
,现在三人同时射击目标,则目标被击中的概率为______. 0.75
解:
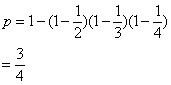
15.已知数列![]() 满足:
满足:![]() ,则使
,则使![]() 成立的
成立的![]() 的值是 . 21
的值是 . 21
解:
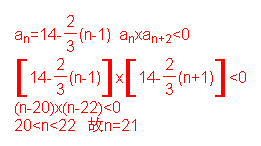
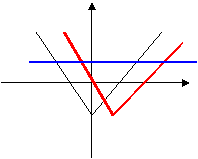
16.永州电视台为某个广告公司特约播放赵本山的两个小品。其中小品甲播映时间为20分钟,广告时间为1分钟,收视观众为60万,小品乙播映时间为10分钟,广告时间为1分钟,收视观众为20万。广告公司规定每周至少有6分钟广告,而电视台每周只能为该公司提供不多于86分钟的节目时间。为获得最高的收视率,电视台每周应播映小品甲 次, 小品乙 次。 2,4。
.设小品甲播映x次,小品乙播映y次. 则有
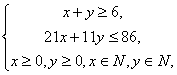
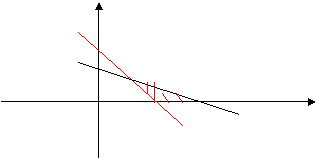
要使收视率最高,则只要z=60x+20y最大即可,由右图可知,当x=2,y=4时,z=60x+20y取得最大值200万.
故电视台每周小品甲和小品乙各播映4集和2集,其收视率最高.
 |
三、解答题:(本大题共6小题,共74分)
17.(本小题满分12分)
已知函数f(x)=2cos2x+![]() sin2x+a.若x∈[0,
sin2x+a.若x∈[0,![]() ],且f(x)<2,求实数a的取值范围.
],且f(x)<2,求实数a的取值范围.
![]() 解:f(x)=cos2x+
解:f(x)=cos2x+![]() sin2x+a+1=2sin(2x+
sin2x+a+1=2sin(2x+![]() )+a+1. 3分
)+a+1. 3分
![]() ∵0≤x≤
∵0≤x≤![]() ,∴
,∴![]() ≤2x+
≤2x+![]() ≤
≤![]() , 5分
, 5分
![]() ∴a≤f(x)≤a+3. 7分
∴a≤f(x)≤a+3. 7分
![]() 又f(x)<2,∴[a,a+3]
又f(x)<2,∴[a,a+3]![]() (-2,2) 9分
(-2,2) 9分
![]() 于是
于是![]() ,解出-2<a<-1. 12分
,解出-2<a<-1. 12分
![]()
 18.(本小题满分12分)
18.(本小题满分12分)
 如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
(1)求BN的长;
(2)求直线BA1与CB1所成角的余弦值
(3)求证:A1B⊥C1M.
![]()
 解:解法一:(传统解法略写)
解:解法一:(传统解法略写)
解法二:
![]() (1)以C为原点CA所在直线为x轴,CB所在直线为y轴,CC1所在直线为z轴,建立空间直角坐标系O-xyz. 2分
(1)以C为原点CA所在直线为x轴,CB所在直线为y轴,CC1所在直线为z轴,建立空间直角坐标系O-xyz. 2分
则B(0,1,0),N (1,0,1),
![]() 可求得
可求得![]() =
=![]() ; 4分
; 4分
(2)由A1(1,0,2)、B(0,1,0)、C(0,0,0)、B1(0,1,2),
![]() 得
得![]() =(1,-1,2),
=(1,-1,2),![]() =(0,1,2), 6分
=(0,1,2), 6分
![]() 从而得cos<
从而得cos<![]() >=
>=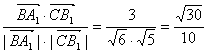 ; 8分
; 8分
(3)又C1(0,0,2)、M(0.5,0.5,2),
![]() 得
得![]() =(-1,1,-2),
=(-1,1,-2),![]() =(0.5,0.5,0) 10分
=(0.5,0.5,0) 10分
所以![]() ·
·![]() =-0.5+0.5+0=0,
=-0.5+0.5+0=0,
![]() 所以
所以![]() ⊥
⊥![]() .
12分
.
12分
19(本小题满分12分)
新田一中高三文科一班学生开展研究性学习活动,他们在学校大门口观察发现:有A、B、C三辆公汽按A、B、C顺序依次连续不断在校门口载客;候车人中大约有三分之一是学生。公汽公司为鼓励学生乘车,每月给第一个乘坐公汽的学生免收一个月的乘车费。你认为乘坐哪一辆公汽最有可能免收一个月的乘车费?并说明理由。
解:A辆公汽乘运第一个学生的概率:
![]()
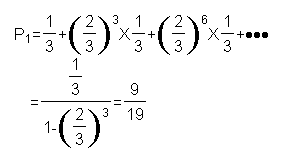 6分
6分
B辆公汽乘运第一个学生的概率:
P2=(![]() )·(
)·(![]() )+(
)+(![]() )4·(
)4·(![]() )+(
)+(![]() )7·(
)7·(![]() )+…
)+…
![]() =
=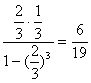 ; 9分
; 9分
C辆公汽乘运第一个学生的概率:
P3=1-![]()
P1>P2>P3
![]() 故乘坐A辆公汽最有可能免收一个月的乘车费
12分
故乘坐A辆公汽最有可能免收一个月的乘车费
12分
20.(本小题满分12分)
已知![]() ,设
,设 ![]()
![]() ,
,
试寻求使得![]() 都成立的
都成立的![]() 的集合.
的集合.
解:由题意得:
![]()
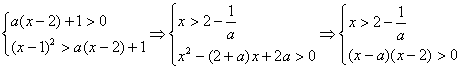 4分
4分
![]() 若
若![]() :则有
:则有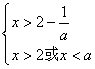 ,而
,而![]() ,所以
,所以![]() ,
,
故![]() ;
8分
;
8分
![]() 若
若![]() :则有
:则有![]() ;
10分
;
10分
![]() 若
若![]() :则有
:则有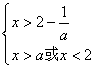 ,故
,故![]() . 12分
. 12分
![]()
![]()
![]()
![]() 21.(本小题满分12分)如图,点F(a,0)(a>0),点P在y轴上运动,M在x轴
21.(本小题满分12分)如图,点F(a,0)(a>0),点P在y轴上运动,M在x轴
上,N为动点,且![]() 0.
0.
(1)求点N的轨迹C的方程;
(2)过点F(a,0)的直线l(不与x轴垂直)与曲线C交于A、B两点,设点
![]()
![]() K(-a,0),
K(-a,0),![]() 与
与![]() 的夹角为θ ,
求证0<θ <
的夹角为θ ,
求证0<θ <![]() .
.

解:.(1)设N(x,y)
![]() 由
由![]() =0,即P是MN的中点,∴M(-x,0),P(0,
=0,即P是MN的中点,∴M(-x,0),P(0,![]() ),
2分
),
2分
![]() ∵
∵![]() =0,∴PM⊥PF,
4分
=0,∴PM⊥PF,
4分
![]() ∴
∴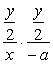 =-1, ∴y2=4ax即为所求.
6分
=-1, ∴y2=4ax即为所求.
6分
(2)设l的方程为y=k(x-a),
![]() 由
由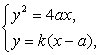 消去x,得y2-
消去x,得y2-![]() y-4a2=0,
8分
y-4a2=0,
8分
![]() 设A(x1,y1),B(x2,y2), 则y1y2=-4a2,
9分
设A(x1,y1),B(x2,y2), 则y1y2=-4a2,
9分
![]()
![]() =(x1+a,y1),
=(x1+a,y1),![]() =(x2+a,y2)
10分
=(x2+a,y2)
10分
![]() ·
·![]() =(x1+a)(x2+a)+y1y2=x1x2+a(x1+x2)+a2+y1y2
=(x1+a)(x2+a)+y1y2=x1x2+a(x1+x2)+a2+y1y2
=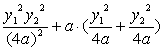 +a2-4a2 =
+a2-4a2 =![]() (y12+y22)-2a2>
(y12+y22)-2a2>![]() (2y1y2)-2a2
(2y1y2)-2a2
![]() =
=![]() ×4a2-2a2=0, ∴cosθ=
×4a2-2a2=0, ∴cosθ=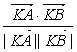 >0,∴0<θ<
>0,∴0<θ<![]() . 12分
. 12分
22.(本小题满分14分)
 如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于点P,交线段AB于点Q,
如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于点P,交线段AB于点Q,
(1)试用t表示切线PQ的方程;
(2)试用t表示出△QAP的面积g(t);若函数g(t)在(m,n)上单调递减,试求出m的最小值;
(3)若S△QAP∈[![]() ,64],试求出点P横坐标的取值围。 .
,64],试求出点P横坐标的取值围。 .
解:(1)设点M(t,t2),又f′(x)=2x,
![]() ∴过点M的切线PQ的斜率为k=2t, 2分
∴过点M的切线PQ的斜率为k=2t, 2分
∴切线PQ的方程为y-t2=2t(x-t),
![]() 即y=2tx-t2. 4分
即y=2tx-t2. 4分
(2)由(1)可求得P(![]() ,0), Q(6,12t-t2)
,0), Q(6,12t-t2)
∴g(t)=S△QAP=![]() (6-
(6-![]() t)(12t-t2)
t)(12t-t2)
![]() =
=![]() t3-6t2+36t,(0<t<
t3-6t2+36t,(0<t<![]() , 6分
, 6分
由于g′(t)=![]() t2-12t+36,
t2-12t+36,
令g′(t)<0,则4<t<12,
又0<t<6,∴4<t<6,
∴g(t)的单调递减区间为(4,6),
![]() 因此m的最小值为4. 9分
因此m的最小值为4. 9分
(3)由(2)得,g(t)在(4,6)上递减,
∴此时S△QAP∈(g(6),g(4))=(54,64),
令g′(t)>0,得0<t<4,
∴g(t)在(0,4)上递增.
∴此时S△QAP∈(g(0),g(4))=(0,64),
又g(4)=64,
![]() ∴函数g(t)的值域为(0,
∴函数g(t)的值域为(0,![]() .
12分
.
12分
由![]() ≤g(t)≤64,得1≤t<6,
≤g(t)≤64,得1≤t<6,
∴![]() ≤
≤![]() <3,
<3,
![]() ∴点P的横坐标∈[
∴点P的横坐标∈[![]() ,
,![]() . 14分
. 14分