高三年级第二次质量检测数学试题
(理科)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分150分.考试时间120分钟.
|
如果事件A、B互斥,那么
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么
P(A·B)=P(A)·P(B)
第I卷
一、选择题:本大题共12小题;每小题5分,共60分. 在每小题给出的四个选项中, 只有
一项是符合题目要求的.
1.已知函数![]() ,则集合
,则集合![]() 中含
中含
有元素的个数为 ( )
A.0 B.1或0 C.1 D.1或2
2.如果复数![]() (其中
(其中![]() 为虚数单位,
为虚数单位,![]() 为实数)的实部和虚部是互为相反数,那么
为实数)的实部和虚部是互为相反数,那么![]() 等
等
于 ( )
A.![]() B.
B.![]() C.2 D.-
C.2 D.- ![]()
3.如果平面![]() 平面
平面![]() ,且交线为
,且交线为![]() 的 ( )A.充分非必要条件 B.必要非充分条件
的 ( )A.充分非必要条件 B.必要非充分条件
C.充要条件 D.即不充分又不必要条件
4.已知函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() ,那么
,那么![]() 的值为
的值为
( )
A.2 B.-2 C.3 D.-3
5.若抛物线![]() 上三点的横坐标的平方成等差数列,那么这三点到焦点的距离
上三点的横坐标的平方成等差数列,那么这三点到焦点的距离
为 ( )
A.成等差数列 B.成等比数列
C.不成等差也不成等比数列 D.成常数列
6.在空间四边形ABCD中,连结AC、BD若△BCD是正三角形,且E为其中心,则
![]() 的化简结果是 ( )
的化简结果是 ( )
A.![]() B.2
B.2![]() C.
C.![]() D.
D.![]()
7.![]() 的值等于 ( )
的值等于 ( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
8.如果一个三位正整数形如“![]() ”满足
”满足![]() ,则称这样的三位数为凸数
,则称这样的三位数为凸数
(如120、363、374等),那么所有凸数个数为 ( )
A.240 B.204 C.729 D.920
9.设F1、F2是双曲线![]() 的两个焦点,P在双曲线上,若
的两个焦点,P在双曲线上,若![]()
![]() 为半焦距)则双曲线的离心率为 ( )
为半焦距)则双曲线的离心率为 ( )
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
10.已知![]() 的值为 ( )
的值为 ( )
|
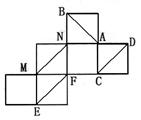
11.一个正方体纸盒展开后如图,在原正方体纸盒中有下列
结论①AB⊥EF ②AB与CM成60° ③EF与MN
是异面直线 ④MN//CD
其中正确的是 ( )
A.①② B.③④
C.②③ D.①③
12.北京市为成功举办2008年奥运会,决定从2003年到2007年5年间更新市内现有全
部出租车,若每年更新的车辆数比前一年递增10%,则2003年底更新车辆数约为现有
总车辆数的(参考数据1.14=1.46 1.15=1.61) ( )
A.10% B.16.4% C.16.8% D.20%
第Ⅱ卷
二、填空题:本大题共4小题;每小题4分,共16分 . 把答案填在题中横线上.
13.已知A(-4,0),B(2,0)以AB为直径的圆与![]() 轴的负半轴交于C,则过C点的圆
轴的负半轴交于C,则过C点的圆
的切线方程为 .
14.关于![]() 的方程
的方程![]() 的两根分别在区间(0,1)与(1,2)内.则
的两根分别在区间(0,1)与(1,2)内.则![]() 的
的
取值范围是 .
15.自半径为R的球面上一点P引球的两两垂直的弦PA、PB、PC,则PA2+PB2+PC2
= .
16.定义运算“*”对于![]() 满足以下运算性质:①1
满足以下运算性质:①1![]() 1=1 ②(n+1)
1=1 ②(n+1)![]() 1=3(n
1=3(n![]() 1)则
1)则
![]() 的表达式为
.
的表达式为
.
三、解答题:本大题6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知:甲盒子内有3个正品元件和4个次品元件,乙盒子内有5个正品元件和4个次品元件,现从两个盒子内各取出2个元件,试求
(Ⅰ)取得的4个元件均为正品的概率;
(Ⅱ)取得正品元件个数![]() 的数学期望.
的数学期望.
(参考数据:4个元件中有两个正品的概率为![]() ,三个正品的概率为
,三个正品的概率为![]() )
)
18.(本小题满分12分)
已知:![]() 为常数)
为常数)
(1)若![]() ,求
,求![]() 的最小正周期;
的最小正周期;
(2)若![]() 在[
在[![]() 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求![]() 的值;
的值;
(3)在(2)条件下![]() 先按
先按![]() 平移后再经过伸缩变换后得到
平移后再经过伸缩变换后得到![]() 求
求![]() .
.
19.(本小题满分12分)
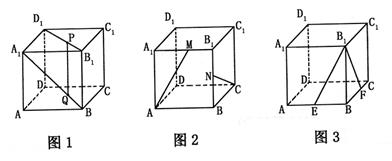
在棱长为1的正方体ABCD—A1B1C1D1中
(Ⅰ)P、Q分别是B1D1、A1B上的点且B1P=![]() B1D1,BQ=
B1D1,BQ=![]() A1B (如图1).
A1B (如图1).
求证PQ//平面AA1D1D;
(Ⅱ)M、N分别是A1B1、BB1的中点(如图2)求直线AM与CN所成的角;
(Ⅲ)E、F分别是AB、BC的中点(如图3),试问在棱DD1上能否找到一点H,使BH⊥
平面B1EF?若能,试确定点H的位置,若不能,请说明理由.
|
20.(本小题满分12分)
函数![]() )
)
(1)已知![]() 的展开式中
的展开式中![]() 的系数为
的系数为![]() ,求常数
,求常数![]()
(2)是否存在![]() 的值,使
的值,使![]() 在定义域中取任意值时,
在定义域中取任意值时,![]() 恒成立?如存在,求出
恒成立?如存在,求出![]() 的
的
值,如不存在,说明理由.
21.(本小题满分12分)
一椭圆中心在原点,右焦点为F(2,0),离心率为![]() ,A为椭圆最大的内接矩形在第一象限的顶点,内接矩形的边平行椭圆对称轴.
,A为椭圆最大的内接矩形在第一象限的顶点,内接矩形的边平行椭圆对称轴.
(1)求A点坐标;
(2)过F的弦![]() 作平行四边形
作平行四边形![]() 求点P的轨迹方程;
求点P的轨迹方程;
(3)![]() 是不是矩形,如果是,写出相应的直线
是不是矩形,如果是,写出相应的直线![]() 的方程,如果不是,说明理由.
的方程,如果不是,说明理由.
22.(本小题满分14分)
若Sn和Tn分别表示数列{![]() 和
和![]() 的前
的前![]() 项和,对任意正整数
项和,对任意正整数![]()
Tn-3Sn=4![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)在平面直角坐标系内,直线![]() 的斜率为
的斜率为![]() .且与曲线
.且与曲线![]() 有且仅一个交点,与
有且仅一个交点,与
![]() 轴交于Dn,记
轴交于Dn,记![]() 求
求![]() ;
;
(Ⅲ)若![]()
高三年级第二次质量检测
数学试题(理科)参考答案
一、选择题:1—5 BDBAA 6—10 CCABB 11—12 DB
二、填空题:13.![]() 14.
14.![]() 15.4R2 16.3n-1
15.4R2 16.3n-1
三、解答题:17.解:(I)从甲盒中取两个正品的概率为P(A)=![]() ……2分
……2分
从乙盒中取两个正品的概率为P(B)=![]() ……4分
……4分
∵A与B是独立事件 ∴P(A·B)=P(A)·P(B)=![]() ……6分
……6分
(II)![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 | 3 |
| ||
| P |
|
|
|
|
|
![]() ……12分
……12分
18.解:![]() ……2分
……2分
(1)最小正周期![]() ……4分
……4分
(2)![]()
![]() ……6分
……6分
|
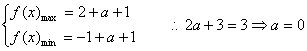 ……8分
……8分
![]() (3)
(3)![]()
![]() ……10分
……10分
![]() ……12分
……12分
19.解:(I)解法一:在A1D1上取点P1,AA1上取点Q,使A1P1=![]() A1D1,
A1D1,
AQ1=![]() AA1,由已知B1P:PD=A1P1:P1D1=1:2
AA1,由已知B1P:PD=A1P1:P1D1=1:2
∴PP1//A1B1 且PP1=![]() AB……2分 在平面AA1B1B中同理可证1//AB,
AB……2分 在平面AA1B1B中同理可证1//AB,
|
AA1D1D……4分
解法二:以D为原点,如衅建立空间直角坐标系,则下列各点的坐标为:
D1(0,0,1) B1(1,1,1) A1(1,0,1) B(1,1,0)
由已知P![]() ……2分
……2分
在A1D1,AA1上取点P1,Q1 :A1P1:A1D1=1:3 AQ1:AA1=1:3则由定比分点公式得
P1(![]() Q1(1,0,
Q1(1,0,![]() )
) ![]()
![]() ∴PQ//平面AA1D1D……4分
∴PQ//平面AA1D1D……4分
(II)解法一 取AB中点![]() ,CC1中点
,CC1中点![]() 连B
连B![]() 、
、![]()
![]() 、
、![]() B,则AM//B
B,则AM//B![]()
CN//B1![]() ∴∠
∴∠![]() B
B![]() 即为AM与CN所成的角.……6分
即为AM与CN所成的角.……6分
在△B![]()
![]() 中,B
中,B![]() =B
=B![]() =
=![]()
由余弦定理得![]() ,∴AM与CN所成的角为
,∴AM与CN所成的角为![]() ……8分
……8分
解法二 以D为原点如图建立空间直角坐标系,下列各点坐标为A(1,0,0)
M(1,![]() N(1,1,
N(1,1,![]() ) C(0,1,0)
) C(0,1,0) ![]() ……6分
……6分
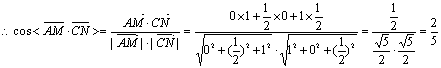
∴AM与CN所成角为![]() ……8分
……8分
(Ⅲ)解法一 能找到点H ∵H∈DD1 ∴BH的射影为BD则BH⊥EF,恒成立,若BH⊥平
面BEF,则HB⊥B1F必成立,设H在BB1C1C内射影为H1,BH1⊥B1F必成立.…10分
设BH1交B1F于G ∵∠BB1G=30° 则∠B1BG=60° ∠GBC=90°-60°=30°
∴CH1=![]() BC=
BC=![]() CC1 即H1是CC1中点……12分
CC1 即H1是CC1中点……12分
∴H也必是DD1中点,∴这样的点存在且是DD1之中点
解法二 以D为原点如图建立空间直角坐标系,设H坐标为(0,0,![]() ),B1(1,1,1)
),B1(1,1,1)
B(1,1,0) F(![]() ,1,0) BH⊥EF恒成立(如方法一)
,1,0) BH⊥EF恒成立(如方法一)
若BH⊥平面B1EF,BH⊥B1F 即![]() ……10分
……10分
又![]()
![]()
故存在点H是DD1之中点……12分
20.解(1)Tr+1=C![]() 由
由![]() 解得
解得![]() ……3分
……3分
![]()
![]() ……6分
……6分
(2)![]() 要使(
要使(![]()
只需![]() ……8分 10当
……8分 10当![]() 时,设
时,设![]()
![]()
|
| (0, |
| ( |
|
| — | 0 | + |
|
|
| 极小值 |
|
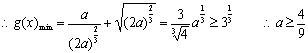 ……10分
……10分
20当![]() 时,不成立 30当
时,不成立 30当![]() 时,不成立 故当
时,不成立 故当![]() ……12分
……12分
另解法 ![]() 只需
只需![]()
21.解:(1)![]() ∴椭圆方程:
∴椭圆方程:![]() ……2分
……2分
设A(![]() 得1=
得1=![]() 当且仅当
当且仅当
![]() 时“=”成立A(
时“=”成立A(![]() ,1)……4分
,1)……4分
或设![]()
![]()
当![]() 时
时 ![]() 取最大值为
取最大值为![]()
![]()
(2)设P(![]() 为所求轨迹上一点,平行四边形对称中心为(
为所求轨迹上一点,平行四边形对称中心为(![]() ……5分
……5分
设![]() 得
得![]()
![]() ①
①
而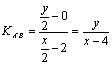 ② 将②代入①化简得
② 将②代入①化简得
![]()
∴A在圆内.……8分
(3)若![]() 轴,得
轴,得![]() 相应的OA′PB′不是矩形
相应的OA′PB′不是矩形
设![]() 联立有
联立有![]()
![]() ……10分
……10分
即![]()
![]() 即
即![]() 舍去
舍去
![]() 故矩形存在,
故矩形存在,![]() 方程为
方程为![]() ……12分
……12分
22.解:(I)![]()
![]() ……2分 当
……2分 当![]()
当![]() ……4分
……4分
(II)设![]()
![]() 由
由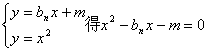 由于仅有一个公共点.
由于仅有一个公共点.
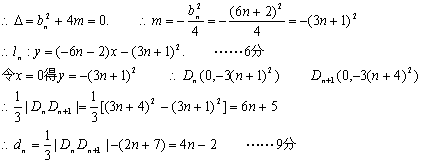
(III)![]() ……12分
……12分