高三年级第六次月考数学试卷
（总分：150分 时量：120分钟 ）
一．选择题（每小题5分，共60分）
1．已知函数f (x)的图象恒过点(1，1)，则f (x－4)的图象过
A．(－3，1) B．(1，5) C．(1，－3) D．(5，1)
2．(理)下列求导正确的是
A．
B．
C．
=3x·log3e
D．
=－2xsinx
(文)函数
，
的值域是
（
）
（
）
（
）
（
）
3．（理）如果ξ是离散型随机变量，η=3ξ+2，那么 （ ）
（A）Eη=3Eξ+2，Dη=9Dξ （B）Eη=3Eξ，Dη=3Dξ+2
（C）Eη=3Eξ+2，Dη=9Eξ+4 （D）Eη=3Eξ+4，Dη=3Dξ+2
（文）设点P是曲线
上的任意一点，P点处切线倾斜角为α，则角α的取值范围是 （
）
A．
B．
C．
D．
4．在抛物线
上，横坐标为4的点到焦点的距离为5，则p的值为（ ）
A. 
B.
1 C.
2 D.
4
5．（理）60°的二面角的一个面所在的平面内有一条直线与二面角的棱成60°的角，则此直线与二面角的另一个面所在的平面所成的角的正弦值是（ ）
A．
B．
C．
D．1
（文）甲命题：平面α⊥平面β，平面β⊥平面γ，则平面α//平面γ；乙命题：平面α上不共线的三点到平面β的距离相等，则α//β。则（ ）
A．甲真乙真 B．甲真乙假 C．甲假乙真 D．甲假乙假
6．若向量
、
的坐标满足
，
，则·等于
7．圆
与
轴交于、两点，圆心为
，若
，则实数
等于
1 B -11
C 9 D 11
8．（理）计算机是将信息转换成二进制进行处理的，所谓二进制即“逢二进一”，如(1101)2表示二进制的数，将它转换成十进制数的形式是1×23+1×22+0×21+1×20=13，那么将二进制数
转换成十进制数是
A.217－2 B.216－1 C.216－2 D.215－1
（文）若 x≤2，y≤2 则目标函数 z=x+2y的取值范围是（ ）
x+y≥2
A．[2，6] B．[2，5] C．[3，6] D．[3，5]
9．设m=37+
·35+
·33+
·3,n=
·36+
·34+
·32,则m－n等于
A.0 B.127 C.128 D.129
10．把英语单词“error”中字母的拼写顺序写错了，则可能出现的错误种数是
A.20 B.19
C.10 D.9
11．甲、乙两名篮球运动员，各自的投篮命中率分别为0.7与0.8，如果每人投篮两次. 甲比乙多投进一次的概率为 （ ）
A 0.1568 B 0.1204 C 0.1736 D 0.042
12.在有太阳的时候，一个大球放在地面上，球的影子伸到距球与地面的接触点10米处，同一时刻，一根长1米，一端接触地面而垂直于地面的尺子的影子长度是2米，则球的半径是
A.2.5米 B.10
－20米
C.6－
米 D.9－4米
二．填空题（每小题4分，共16分）
13．（理）在△ABC中，已知
，a、b、c分别为角A、B、C所对的边，则
的值等于
.
（文）若把抛物线y=2x2绕其顶点逆时针方向转动90°，则转动后所得的抛物线的焦点坐标为 。
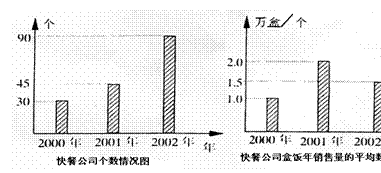14．一个高中研究性学习小组对本地区2000年至2002年快餐公司发展情况进行了调查，制成了该地区快餐公司个数情况的条形图和快餐公司盒饭年销售量的平均数情况条形图（如图），根据图中提供的信息可以得出这三年中该地区每年平均销售盒饭 万盒.
15．一个等差数列共n项，其和为90，这个数列的前10项的和为25，后10项的和为75，则项数n为___________
16.(理)下列命题：
(1)如果平面γ与两个平面α、β所成的二面角都是直二面角，则α∥β.
(2)函数y=sinx在第一象限是增函数.
(3)函数y=tg
-ctg的最小正周期是π.
(4)奇函数y=f(x)在定义域R上满足f(1+x)=f(1-x)，则y=f(x)是以4为周期的周期函数.
其中正确命题的序号是 .
（文）
的值为____________
三．解答题
17．（本小题满分12分）
已知
，解关于
的不等式
．
18．（本小题满分12分）
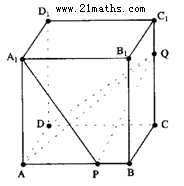如图棱长是1的正方体，P、Q分别是棱AB、CC1上的内分点，满足
.
（1）求证：A1P⊥平面AQD；
（2）求直线PQ与平面AQD所成角的正弦值.
19．（本小题满分12分）
已知：
、
、
是同一平面内的三个向量，其中=（1，2）
（Ⅰ）若
，且//，求的坐标；
（Ⅱ）若=
且
与
垂直，求与的夹角θ.
20、（本小题满分14分）
某村2002年底全村共有1000人，全年工农业总产值为840万元．
（I）若从2003年起该村每年的工农业总产值较上年增加14 万元，每年人口较上年净增数相同，要使该村人均产值年年都增长，那么该村每年人口的净增不超过多少人？
（II）若从2003年起该村每年工农业总产值较上年增长
，每年人口较上年净增10人，则到2012年该村能否实现年人均产值较2002年翻一番（增加一倍）的经济发展目标？
21、（理）已知函数f(x)=a0+a1=x+a2x2+a3x3+…+anxn(n∈Nn)，且y=f(x)的图象经过点(1，n2)，数列{an}(n∈N+)为等差数列。
(1)求数列{an}的通项公式；
(2)当n为奇函数时，设g(x)=
,是否存在自然数m和M，使不等式m<g(
)<M恒成立，若存在，求出M-m的最小值；若不存在，说明理由。
（文）设函数f(x)=sin2x+2a·cosx+a3-a(0≤x≤
)
(1)求f(x)的最大值M(a)。
(2)当a∈[-1，1]时，求函数M(a)的最值。
22．(本小题满分12分)
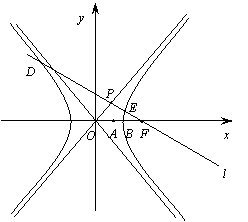
已知双曲线:
，是右顶点,
是右焦点, 点在轴正半轴上，且满足
成等比数列,过作双曲线在第一、三象限的渐近线的垂线
，垂足为．
（Ⅰ）求证：
；
（Ⅱ）若与双曲线的左、右两支分别相交于点、
，求双曲线的离心率
的取值范围．
高三年级第六次月考数学试卷答案
一．选择题。
（理）DBACB ABBDB CB
（文）DDACD ABBDB CB
二．填空题：
（13）1 （文 ） 
（14）
85
（15） 18
（16） ③④ （文）2
17解当
时，原不等式的解集为
；当
时，原不等
式的解集为
；故当
时，原不等式的解集为
18．解：（本小题满分12分）
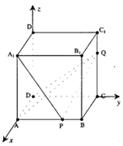解法（一）（1）以D为原点，DA、DC、DD1所在直线分别
为x、y、z轴建立空间直角坐标系0－xyz则D（0，0，0），A（1，0，0）， B（1，1，0），
A1（1，0，1），C1（0，1，1），P（1，
），Q（0，1，
），
， 
（2）
设PQ与平面AQD所成角为θ，
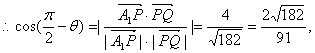则直线PQ与平面AQD所成角的正弦值是
19． （Ⅰ）设
由
得 
或 
∴
（Ⅱ）
（※）
代入（※）中, 
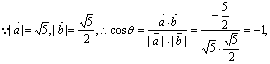
20．解：（1）设从2002年起的第
年（2002年为第一年），该村的人均产值为
，
每年人口较上年净增数为
，则
，…………………… 3分
则
， …………………………5分
当且仅当
，即
时，随着的增大而增大，
故要使该村人均产值年年都增长，那么该村每年人口的净增不超过16人．……７分
（另法：由
恒成立求解）
（2）由2002年该村的人均产值为
万元;
2012年该村的人均产值为
万元，………………………………… 9分
从而
,
故到2012年该村能够实现年人均产值较2002年翻一番的经济发展目标．……12分
22(本小题满分12分)
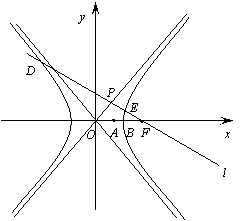已知双曲线:，是右顶点,是右焦点, 点在轴正半轴上，且满足成等比数列,过作双曲线在第一、三象限的渐近线的垂线，垂足为．
（Ⅰ）求证：；
（Ⅱ）若与双曲线的左、右两支分别相交于点、，求双曲线的离心率的取值范围．
21、解：（Ⅰ）法一．
，
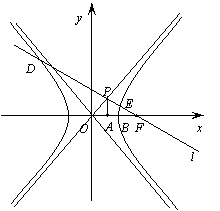
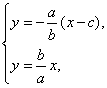解得
…2分
|
|
|
|
|
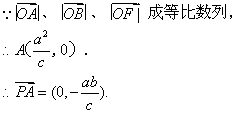
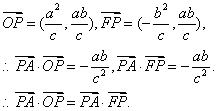
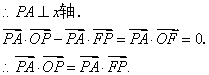
（Ⅱ）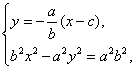
|
|
|
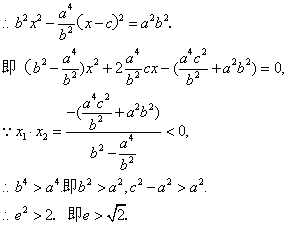
21、已知函数f(x)=a0+a1=x+a2x2+a3x3+…+anxn(n∈Nn)，且y=f(x)的图象经过点(1，n2)，数列{an}(n∈N+)为等差数列。
(1)求数列{an}的通项公式；
(2)当n为奇函数时，设g(x)=,是否存在自然数m和M，使不等式m<g()<M恒成立，若存在，求出M-m的最小值；若不存在，说明理由。
解：(1)据题意：f(1)=n2 即a0+a1+a2+……+an=n2
令n=1 则a0+a1=1，a1=1-a0
令n=2 则a0+a1+a2=22，a2=4-(a0+a1)=4-1=3
令n=3 则a0+a1+a2+a3=32，a3=9-(a0+a1+a2)=9-4=5
∵{an}为等差数列 ∴d=a3-a2=5-3=2
a1=3-2=1 a0=0 an=1+(n-1)·2=2n-1
(2)由(1)f(x)=a1x1+a2x2+a3x3+…+anxn
n为奇数时，f(-x)=-a1x1+a2x2-a3x3+…+an-1xn-1-anxn
g(x)=
相减得 
∴
令
∵
∴Cn+1≤Cn，Cn随n增大而减小
又
随n增大而减小
∴g()为n的增函数，当n=1时，g()=
而
∴使m<g()<M恒成立的自然m的最大值为0，M最小值为2。
M-m的最小值为2。