高三年级第四次月考数学试卷
(文理合卷)
一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的):
1、已知直线l的倾斜角为![]() ,且经过点P(0,-2),则直线l的方程是( )
,且经过点P(0,-2),则直线l的方程是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2、圆![]() 的圆心到直线
的圆心到直线![]() 的距离是( )
的距离是( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
3、设集合![]() ,若
,若![]() ,则实数m的取值范围是( )
,则实数m的取值范围是( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
4、若函数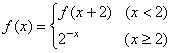 ,则
,则![]() 的值为( )
的值为( )
(A) 2 (B)
8 (C) ![]() (D)
(D) ![]()
5、在等比数列{an}中,a3=3,S3=9,则a1的值是( )
(A) 3 (B) 12 (C) –6或12 (D) 3或12
6、(理科做)从8盆不同的鲜花中选出4盆摆成一排,其中甲、乙两盆不同时展出的摆法种数为( )
(A) 1320 (B) 960 (C) 600 (D) 360
(文科做)从8盆不同的鲜花中选出4盆摆成一排,其中甲、乙两盆中有且仅有一盆展出的摆法种数为( )
(A) 1320 (B) 960 (C) 600 (D) 360
7、已知![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() ,则使向量
,则使向量![]() 与
与![]() 的夹角为钝角的实数
的夹角为钝角的实数![]() 的取值范围是( )
的取值范围是( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D) ![]()
8、若二次函数![]() 和
和![]() 的值域分别为M和N,则集合M和N必定有( )
的值域分别为M和N,则集合M和N必定有( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
9、(理科做)已知曲线![]() 与其关于点(1,1)对称的曲线有两个不同的交点A和B,如果过这两个交点的直线的倾斜角是
与其关于点(1,1)对称的曲线有两个不同的交点A和B,如果过这两个交点的直线的倾斜角是![]() ,则实数a的值是( )
,则实数a的值是( )
(A) 1 (B) ![]() (C) 2 (D)
3
(C) 2 (D)
3
(文科做)曲线![]() 的长度是( )
的长度是( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
10、(理科做)双曲线![]() 的左、右焦点分别为F1、F2,过焦点F2且垂直于x轴的弦为AB,若
的左、右焦点分别为F1、F2,过焦点F2且垂直于x轴的弦为AB,若![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(文科做)若椭圆![]() 和双曲线
和双曲线![]() 有相同的焦点F1、F2,P是两曲线的交点,则
有相同的焦点F1、F2,P是两曲线的交点,则![]() 的值是( )
的值是( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
11、在市场价格调控中,已知某商品零售价2003年比2002年上涨25%,欲控制2004年比2002年只上涨10%,则2004年比2003年应降价( )
(A) 15% (B) 12% (C) 10% (D) 5%
12、方程![]() 所表示的曲线是( )
所表示的曲线是( )
(A) 双曲线 (B) 抛物线 (C) 椭圆 (D) 不能确定
二、填空题(本大题共4小题,每小题4分,共16分):
13、若抛物线![]() 的焦点在圆
的焦点在圆![]() 的外部,则实数m的取值范围是
。
的外部,则实数m的取值范围是
。
14、在![]() 的展开式中,
的展开式中,![]() 项的系数是 。
项的系数是 。
15、(理科做)有一系列椭圆,满足条件:①中心在原点;②以直线x=2为准线;③离心率![]() ,则所有这些椭圆的长轴长之和为 。
,则所有这些椭圆的长轴长之和为 。
(文科做)若椭圆![]() =1的离心率为
=1的离心率为![]() ,则k的值为 。
,则k的值为 。
16、已知点![]() 是函数
是函数![]() 上的两个不同点,且
上的两个不同点,且![]() ,试根据图像特征判定下列四个不等式的正确性:①
,试根据图像特征判定下列四个不等式的正确性:①![]() ;②
;②![]() ;③
;③![]()
![]() ;④
;④![]() 。其中正确不等式的序号是
。
。其中正确不等式的序号是
。
三、解答题(本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤):
17、(本小题满分12分)已知角![]() 的顶点与直角坐标系的原点重合,始边在x轴的非负半轴上,终边经过点P(
的顶点与直角坐标系的原点重合,始边在x轴的非负半轴上,终边经过点P(![]() ,2 );又角
,2 );又角![]() 满足关系式
满足关系式![]() =
=![]() ;求:
;求:
⑴
![]() 的值; ⑵
的值; ⑵ ![]() 的值。
的值。
18、(本小题满分12分)已知定线段AB的端点为A(1,3)、B(5,2),动直线l:![]() 与线段AB交于点P,求实数t的取值范围。
与线段AB交于点P,求实数t的取值范围。
19、(本小题满分12分)若定义在R上的函数f(x)为奇函数,且在![]() 上是增函数。
上是增函数。
⑴ 求证:f(x)在![]() 上也是增函数;
上也是增函数;
⑵ 对任意![]() ,求实数m,使不等式
,求实数m,使不等式![]() 恒成立。
恒成立。
20、(本小题满分12分)
(理科做)某药厂生产A、B两类药片,其中A类药片每片含的有效成份为: 阿司匹林2mg、小苏打5mg、可待因1mg,每片价格为0.1元;B类药片每片含的有效成份为: 阿司匹林1mg、小苏打7mg、可待因6mg,每片价格为0.2元。若至少要求提供阿司匹林12mg、小苏打70mg、可待因28mg,则两类药片的最小总数是多少?怎样搭配价格最低?
(文科做)某工厂用两种不同原料生产同一产品,若采用甲种原料,每吨成本1000元,运费500元,可得产品90千克;若采用乙种原料每吨成本1500元,运费400元,可得产品100千克;今每日预算为总成本不得超过6000元,运费不得超过2000元,问此工厂每日最多可生产多少千克产品?
 21、(本小题满分12分)
21、(本小题满分12分)
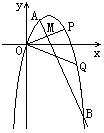
(理科做)如图,过原点O的两条抛物线的弦OP、OQ与x轴的夹角均为![]() ,长分别为2和4,
,长分别为2和4,
⑴ 求此抛物线的方程;
⑵ 若OP的中垂线交抛物线于A、B两点,求四边形OAPB的面积。
(文科做)经过抛物线y2=4x的焦点F的直线![]() 与该抛物线交于A、B两点,AB的中点为M,
与该抛物线交于A、B两点,AB的中点为M,
⑴ 若线段AB的斜率为k,试求点M的轨迹方程;
⑵ 若直线![]() 的斜率k>2,且点M到直线
的斜率k>2,且点M到直线![]() 的距离为
的距离为![]() ,试确定m的取值范围。
,试确定m的取值范围。
22、(本小题满分14分)已知定义域为[0,1]的函数f(x)同时满足:①对于任意![]() ,总有
,总有![]() ;②
;②![]() ;③若
;③若![]() ,则有
,则有![]()
![]()
⑴ 求f(0)的值;
⑵ 求函数f(x)的最大值;
⑶(理科做,文科不做)证明:满足上述条件的函数f(x)对一切实数x都有![]() 成立。
成立。
杭师院附高2003学年高三年级第四次月考数学试卷评分标准
一、选择题(每小题5分,共60分):ABDCD ![]() BA
BA
二、填空题(每小题4分,共16分;答案全对得分,否则不得分)
13、![]() 或
或![]() 14、135 15、(理)4 (文) 4或-5/4 16、①③
14、135 15、(理)4 (文) 4或-5/4 16、①③
三、解答题(共76分,按步骤得分)
17、⑴![]() ⑵ 2
⑵ 2
18、若t=0,则动直线不存在,故![]() ;故动直线为:
;故动直线为:![]() 为斜率是-1的平行直线系,
为斜率是-1的平行直线系,
可得过A、B端点的平行直线在y轴上的截距范围是:![]() 即:
即:![]()
19、⑴ 略 ⑵ ![]()
20、(理科题)药品为11片,其中A类药3片,B类药8片时,药的搭配价最低。
(文科题)每日最多可生产440千克产品。
21、(理科题)
⑴ 可得P、Q的坐标分别为![]() ,设抛物线方程为:
,设抛物线方程为:![]() 代入可得抛物线方程为:
代入可得抛物线方程为:![]()
⑵ 可得![]() ,
,![]() ,故
,故![]()
(文科题)
⑴ 可得![]() ,消去k可得中点轨迹方程:
,消去k可得中点轨迹方程:![]()
⑵ 由点到直线的距离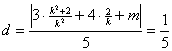
得:![]() ,再由k>2得:
,再由k>2得:![]()
解得:![]() 或
或![]() ,
,
即m的取值范围是:![]()
22、⑴令x1=x2=0,由条件(1)得:f(0)≥0,由条件(3)得: f(0)≤0,故:f(0)=0
⑵先证f(x)在[0,1]上是单调递增函数.
任取0≤x1<x2≤1,可知: x2-x1∈(0,1),则f(x2)=f[(x2-x1)+ x1]≥f(x2-x1)+ f(x1)
所以:f(x2)≥f(x1),于是当0≤x≤1时,有f(x)≤f(1)=1
所以:当x=1时,f(x)MAX=1
⑶(理)证明:
当![]() 时,f(x)≤1<2x(min)<2x, 成立
时,f(x)≤1<2x(min)<2x, 成立
当![]() 时,首先,f(2x)≥f(x)+f(x)=2f(x) 所以:f(x)≤
时,首先,f(2x)≥f(x)+f(x)=2f(x) 所以:f(x)≤![]() f(2x)
f(2x)
显然,当![]() 时,f(x)≤f(
时,f(x)≤f(![]() )≤
)≤![]() f(2*
f(2*![]() )=
)=![]() f(1)=
f(1)=![]() < 2x(min) <2x成立
< 2x(min) <2x成立
下可用数学归纳法可证:当![]() 时均成立
时均成立
当x=0时,f(0)=0=2x
综上可得:满足条件的函数f(x)对![]() 内的任意值总有f(x)≤2x成立.
内的任意值总有f(x)≤2x成立.