高考数学预测试题3
数 学(一)
参考公式：
三角函数的积化和差公式： 正棱台、圆台的侧面积公式
其中
、
分别表示
上、下底面周长，
表示斜高或母线长.
球体的体积公式：
，其中R
表示球的半径.
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
第Ⅰ卷（选择题共60分）
一.选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求的
1．已知全集U ={1，2，3，4，5，6，7}，M ={3，4，5}，N ={1，3，6}，则集合{2，7}等
于 （ ）
A．M∩N
B． 
C． 
D．M∪N
2．点P（x，y）在曲线
上，使
取得最大值的点P的坐标是（ ）
A．（6，－8） B．（－6，8） C．（3，－4） D．（－3，4）
3．若
的夹角为60°，则
等于
( )
A．
B．
C．
D．
4．如图，已知斜三棱柱的侧棱长为，作与侧棱垂直的截面，截得的三角形PQR是边长为
的正三角形，那么它的体积是 （ ）
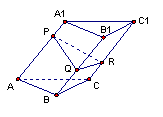A．
B．
C．
D．
5．双曲线
的一条渐近线与直线
垂直，则双曲线的离心率为
A．
B．
C．
D．
（ ）
6.已知
（ ）
A．
B．
C．
D．－
7．函数
的单调递增区间是 （ ）
A．
B．
C．
D．
8．已知函数
与
的图象关于
轴对称，则原点到直线
距离的最大值为
（
）
A、2
B、
C、不确定 D、1
9．已知函数
的最小值是 （ ）
A．
B．2 C．
D．
10．在约束条件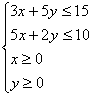
下，目标函数
（ ）
A．有最大值3，最小值0 B．有最大值5，最小值0
C．有最大值
，最小值0 D．有最大值5，最小值2
11．设
的反函数的解析式是 （ ）
A．
B．
C．
D．
12．有3个命题
（1）底面是正三角形，其余各个面都是等腰三角形的棱锥是正三棱锥；
（2）各个侧面都是等腰三角形的四棱锥是正四棱锥；
（3）底面是正三角形，相邻两侧面所成的二面角都相等的三棱锥是正三棱锥。
其中假命题的个数是 （ ）
A．0 B．1 C．2 D．3
高考模拟试题
数 学(一)
第Ⅱ卷（非选择题共90分）
二.填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。
13.函数
在[1，2]上有反函数，则
的一切可取值的范围是
。
14.设圆过双曲线
的一个顶点和焦点，圆心在双曲线上，则圆心到双曲线中心的距离
。
15．设O、A、B、C为平面上四个点，
，
，
，且
，
=
=-1，则
＝__________。
16．给出下列四个命题：
① 函数
为奇函数的充要条件是=0；
② 若凸多面体各个面都是六边形，则2F=V－2（其中F是面数，V是顶点数）；
③ 函数
的反函数是
；
④ 若函数
是偶函数，则函数
的图象关于直线
对称。其中所有正确命题的序号是
.
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或或演算步骤
17．（本小题满分12分）
在△ABC中，已知
且最长边长为1，求角C及△ABC中最短边的长.
18．（本小题满分12分）
甲、乙两人独立解出某一道数学题的概率相同，已知该题被甲或乙解出的概率为0.36，求：
（理科）
（1）甲独立解出该题的概率；
（2）解出该题的人数ξ的数学期望.
（文科）
（1）甲独立解出该题的概率；
（2）甲、乙中有且只有一个解出该题的概率.
19．（本小题满分12分）
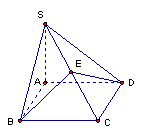
四棱锥S—ABCD的底面是正方形，SA⊥底面ABCD，E是SC上一点.
（1）求证：平面EBD⊥平面SAC；
（2）假设SA=4，AB=2，求点A到平面SBD的距离；
（3）当
的值为多少时，二面角B—SC—D大小为120°.
20．（本小题满分12分）
已知函数
.
（Ⅰ）求函数
的定义域；
（Ⅱ）若函数在[10，+∞]上单调递增，求
的取值范围.
21．（本小题满分12分）
已知直线
经过椭圆
的右焦点F2，且与椭圆C交于A、B两点，若以弦AB为直径的圆经过椭圆的左焦点F1，试求椭圆C的方程.
22．（本小题满分14分）
已知一次函数的图象关于直线
对称的图象为C，且
若点
*）在曲线C上，并有
.
（Ⅰ）求的解析式及曲线C的方程；
（Ⅱ）求数列{
}的通项公式；
（Ⅲ）设
的值.
高考预测试题
数 学(一)
参考答案
一、选择题：本题考查基本知识和基本运算. 每小题5分，满分60分.
1．B .由
={1，2，6,7},
={2，4,5,7}得，={2，7}
2．A . 方法一：由点P（x，y）在曲线上得，
=
=
=
（其中
，
为锐角）
当
时，取得最大值，这时
，
，所以点P的坐标为（6，－8）。
方法二：曲线的普通方程为
的圆，则经过原点和圆心（3，-4）的直线为
。直线与圆的交点就是使得取得最大（小）值的点P（x，y）。
3．D .
=
=
=
=
4．B.将图形的下部分平移到上部，使得下底面与上底面重合，就可以得到一个直三棱柱，其底面是边长为的正三角形，侧棱长（高）为。
5．B.因为双曲线即
的一条渐近线与直线垂直，所以双曲线的一条渐近线为
，从而
，所以
，离心率
=
6．D. 由
，
则
=
=－
7．B.要使函数
=
=2
单调递增，则
，从而有
8．B . 由函数与的图象关于轴对称，得 
，原点到直线距离的为最大值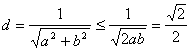
9．C . 在
… ⑴中 用
代换得
……⑵
由⑴⑵得=
10．C.观察图形
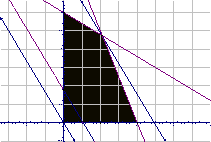
在（0，0）处达到最小值0，在
处达到最大值。
11．B.由 
=
=
得
12．D. （1）（2）（3）假
二、填空题：本题考查基本知识和基本运算.每小题4分,满分16分.
13．(-
，2]U[4，+）. [1，2]在函数的单调区间上,也就是
或
14．
.不妨考虑顶点A(3,0),焦点F(5,0),AF的中垂线为
与双曲线的一个交点M(4,
)为圆心到双曲线中心的距离为.
15．
.
=
.同理
,
=
16．①②③.
三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.
17．解：由已知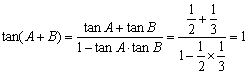
……(3分)
又∠A、∠B是三角形的内角，
∴A+B＜180°
∴∠A+∠B=
，则∠C=
且c边为最长边
∴c = 1 ……(6分 )
∵
∴
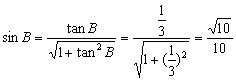
∴b边为最短的边 ……(9分)
由正弦定理得
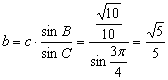
∴∠C为
，最短边为
……(12分)
18．（理）解：（1）设甲、乙独立解出该题的概率为x，
则该题不能被甲或乙解出的概率为（1－x）2 ………………（2分）
由题意可知： 1－（1－x）2=0.36 …………………………（4分）
解得：x=0.2 …………………………………………………（6分）
（2）解出该题的人数ξ的分布列为：
| ξ | 0 | 1 | 2 |
| P | 0.64 | 0.32 | 0.04 |
………（8分）
Eξ=0×0.64+1×0.32+2×0.04=0.4 …………………………………（11分）
答: 该题的人数ξ的数学期望为0.4 ………………………（12分）
（文）解：（1）0.2 （2）0.32 （参照理科的评分标准）
19．解（1）∵正方形ABCD，
∴BD⊥AC，
又∵SA⊥面ABCD，
∴SA⊥BD，则BD⊥面SAC，
又BD
面BED，
∴面BED⊥面SAC …………2分
（2）设
，由三垂线定理得，BD⊥SO.
,
.
设A到面BSD的距离为h，
则
即
即点A到平面SBD的距离为
………(6分)
（3）令ED⊥SC，连接BE，由∠SCB=∠SCD，BC=CD，
∴△BEC≌△ECD.于是BE⊥SC，
则∠BED为二面角B—BC—D的平面角.………………(8分)
SA⊥面ABCD，CD⊥AD，∴CD⊥SD.
设
在
由∠BED=120°，BE=ED，则∠BEO=60°
∴
故当
时，二面角B—SC—D大小为120°…………(12分)
20．（本小题满分12分）
解：（Ⅰ）由
（1）当0<k<1时，得
； ……………(3分)
（2）当k=1时，得
…………………………………(4分)
（3）当k>1时，得
………………(5分)
综上所求函数的定义域：当0<k<1时为
时为
………………………………………………(6分)
（Ⅱ）由
上是增函数 
………………(8分)
又
对任意的
、
，当
时，
有
得：
又
………………………………………………(11分)
综上可知k的取值是（
）……………………………………………………(12分)
（注：第Ⅱ问也可用求导的方法求解。）
21．（本小题满分12分）
设椭圆焦距为2c，则
………(1分 )
，代入y=x+k 得k=－1
……(2分)
将y=x－1代入椭圆方程整理得：
…………(4分)
∵A、B点在直线上，则可设
∵AF1⊥BF1 又F1（－1，0）
…………(7分)
由韦达定理，
解得
……(10分)
为所求方程.
…………(12分)
22．（本小题满分14分）
解（Ⅰ）设
………………………(1分)
……………（2分）
即
①
又
是曲线C的解析式
………………（3分），
因为点
在曲线C上，
所以
，
又
…………………………………（4分）
代入①得
,
∴
………………………………（5分）
曲线C的方程是 
…………………（6分）
（Ⅱ）由（Ⅰ）知当
时，
………（8分）
于是 
………………（10分）
（Ⅲ）因为
……………（11分）
=
………………………（12分）
所以
……（13分）
所以
…………………………………………（14分）