高三数学总复习辅导材料（第27讲）
一、教学进度
高考数学总复习之轨迹问题
主要学习：
求动点的轨迹方程．
二、学习指导
1.掌握直角坐标系中的曲线与方程的关系和轨迹的概念，能够根据所给条件，选择适当的直角坐标系求曲线的方程并画出方程所表示的曲线．
2．“曲线与方程”是解析几何的重要概念．
在直角坐标系中，如果曲线C上的点与一个二元方程f(x，y)＝0的实解有如下关系：
①曲线上的点的坐标都是这个方程的解；
②以这个方程的解为坐标的点都是曲线上的点．
那么，这个方程叫做曲线的方程；这条曲线叫做方程的曲线．
简言之，当组成曲线的点集与方程f(x，y)＝0的解集之间如果能建立起一一对应的关系，则此方程称为曲线的方程，而曲线则是此方程的曲线．
3．掌握求轨迹方程的常用方法：直接法、代入法、交轨法和参数法．
已知曲线，怎样求出它的方程？这是解几学习中常遇到的一个问题．求曲线方程的过程有五个步骤，我们在具体解题时应注意：
①建立直角坐标系时，首先要考虑坐标系的定位问题，图形中的垂直、对称、平行等条件，是定位时必须优先考虑的条件，因为这将有利于后面的计算．
②步骤3是解题的关键步骤，目前初学阶段，一般将条件的几何意义直接代数化(即将几何语言“翻译”成代数语言，常见的有：两点间距离公式、夹角公式等等)即可．
③如果化简过程是同解变形，则证明也就可以省略了；若不是同解变形，如两边同时平方等，则方程解集可能扩大(或缩小)，则应把因化简引起方程解集扩大(或缩小)的部分舍去(或补上)．
三、典型例题
例1．过M(1，3)作两条互相垂直的直线l1和l2，l1与x轴交于A点，l2与y轴交于B点，求线段AB中点的轨迹．
分析：求动点的轨迹可以通过求动点的轨迹方程来解；也可利用平面几何的知识来处理．
例2．已知椭圆
的两个焦点分别是F1、F2，△MF1F2的重心G恰为椭圆上的点，求M的轨迹方程．
分析：求轨迹方程的根本特点就是求出动点的横坐标x与纵坐标y满足的方程，即根据条件建立的等式关系．本题可以考虑用M的坐标表示重心G的坐标，利用G在椭圆上来解．
例3．过圆x2＋y2＝4内一点A(1，0)作圆的弦，求弦的中点M的轨迹方程．
分析：可以看出，弦的中点M由弦所在的直线来决定，而弦所在的直线过定点，即直线仅由延伸方向来确定，故M直线的延伸方向来确定，所以，M的坐标可以用直线的斜率来表示；也可以利用弦中点的几何意义指出轨迹的特征．
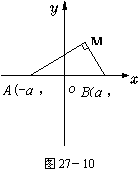
例4．已知点A(－a，0)，B(a，0)（a＞0）．
(1)若动点M与A、B是一个直角三角形的三个顶点，求直角顶点M的轨迹方程；
(2)若动点M满足条件：∠MBA＝2∠MAB，求点M的轨迹方程．
分析：将动点满足的几何条件“坐标化”，即直接将几何条件通过有关定理、公式“翻译”成含有x、y的等式，就得到了轨迹（曲线)的方程．
例5．求与y轴相切，并与圆x2＋y2－4x＝0相外切的动圆圆心M的轨迹方程．
分析：利用圆的切线、两圆外切的的几何意义，找出两点之间的距离和点到直线之间的距离之间的关系，先确定轨迹的几何特征，再写出轨迹方程．
例6．求过点M(1，－1)，离心率为
，且以y轴为准线的椭圆的右焦点F的轨迹方程．
分析：依题意，y轴为椭圆的左准线，现已知e＝，故由椭圆的定义，有
＝e(其中F′为椭圆的左焦点)．因而解本题的关键是寻求椭圆左焦点与右焦点坐标之间的关系．
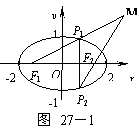
例7．如图27－1，已知椭圆
＋y2＝1的左、右焦点分别为F1和F2，垂直于椭圆长轴的动直线与椭圆的两个交点分别为P1和P2，其中P1的纵坐标为正数，求直线F1P1与F2P2的交点M的轨迹方程．
分析：考虑到P1，P2是椭圆上两个关于x轴对称的点，点M同时在直线F1P1与F2P2上，可利用点M的坐标同时满足直线F1P1，F2P2的方程，消去有关参照量，建立M的轨迹方程．
例8．已知平面内两点M(－1，0)，N(1，0)，若动点P满足MP·MN，PM·PN，NM·NP成等差数列，且公差为负数，求点P的轨迹方程．
分析：将向量的数量积用P的坐标x，y表示，结合三个数成等差数列的等价条件，建立关于x，y的方程，就是P的轨迹．
巩固练习
1．已知椭圆
的两个焦点分别是F1，F2，P是这个椭圆上的一个动点，延长F1P到Q，使得｜PQ｜＝｜F2P｜，求Q的轨迹．
2．动点P到直线x＋4＝0的距离比到定点M(2，0)的距离大2，求点P的轨迹．
3．求与两定圆x2＋y2＝1，x2＋y2－8x－33＝0都相切的动圆圆心的轨迹方程．
4．已知直线l：y＝k(x－5)及圆C：x2＋y2＝16．
(1)若直线l与圆C相切，求k的值；
(2)若直线l与圆C交于A、B两点，求当k变动时，弦AB的中点的轨迹．
5．已知两直线l1：2x－3y＋2＝0，l2：3x－2y＋3＝0，有一动圆M(圆心和半径都在变动)与l1，l2都相交，并且截l1，l2所得的弦长分别是定值26和24，求圆心M的轨迹方程．
6．已知椭圆E经过定点M(1，0)，以直线x＋2＝0为准线，离心率为
，求椭圆E的左顶点的轨迹方程．
7．已知抛物线C：y2＝4x，若椭圆的左焦点及相应准线与抛物线C的焦点F和准线l分别重合（图26－2），求椭圆短轴端点B与焦点F所连线段的中点P的轨迹方程．
8．已知△ABC中，A(－2，0)，B(2，0)，顶点C在直线l：y＝3上移动，求△ABC垂心H的轨迹方程．
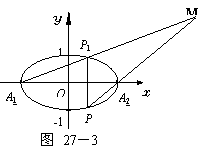
9．如图27－3，已知椭圆＋y2＝1的左、右顶点分别为A1和A2，垂直于椭圆长轴的动直线与椭圆的两个交点分别为P1和P2，其中P1的纵坐标为正数，求直线A1P1与A2P2的交点M的轨迹方程．
10．设x、y∈R，i、j为直角坐标平面内x、y轴正方向上的单位向量，若向量a＝（x＋5）i＋yj，b＝（x－5）i＋yj，且｜a｜－｜b｜＝8．求点M（x，y）的轨迹C的方程．
参考答案
1．解 由题意及椭圆的定义知，｜F1P｜＋｜F2P｜＝4．
∵ ｜PQ｜＝｜F2P｜，∴｜F1Q｜＝4．
∴ Q的轨迹是以F1为圆心，4为半径的圆．
2．解法1 设P(x，y)，则
｜x＋4｜－2＝
．
∵ ≥0，
∴ x≤－6或x≥－2．
当x≤－6时，得
－x－6＝．
两边平方得
x2＋12x＋36＝x2－4x＋4＋y2，
整理，得
y2＝16x＋32≤－96＋32＜0．
与y2≥0矛盾，
∴ x≥－2．
∴
x＋2＝．
两边平方得
x2＋4x＋4＝x2－4x＋4＋y2，
即 y2＝8x．
这就是P点的轨迹方程，它表示一条顶点为原点，焦点是(2，0)的抛物线．
解法2 ∵ P点到直线x＋4＝0的距离比到定点M(2，0)的距离大2，
∴ P点在直线x＋4＝0的右侧．
将直线右移2个单位，得到直线x＋2＝0，则P点到直线x＋2＝0的距离等于到定点M(2，0)的距离，
∴ P点的轨迹是以直线x＋2＝0为准线，定点M(2，0)为焦点的抛物线，其方程为y2＝8x．
3．解 将⊙O1的方程化为(x－4)2＋y2＝49，∴ O1(4，0),r1＝7，设动圆圆心为C(x，y)．
(1) 动圆C与⊙O外切而与⊙O1内切（如图27－4）.
由两圆相切时圆心距与两圆半径之关系，有：
7－O1C＝OC－1，
即 OC＋O1C＝8.
也就是说C点到点O1、O的距离之和等于8．
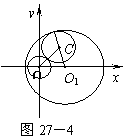由椭圆定义知点C的轨迹是以(0，0)和(4，0)为焦点，长轴长为8的椭圆．
由a＝4，c＝2，得b2＝a2－c2＝12．
∴
动圆圆心C的轨迹方程为
＋
＝1．
(2)当动圆C与⊙O、⊙O1，都内切时，有OC＋O1C＝6．
同理可得动圆圆心C的轨迹方程为
＋
＝1.
4．解 (1) 直线l的方程可化为kx－y－5k＝0，
由题知， 
＝4，
解得
k＝±
．
(2)设弦AB的中点为M．显然，直线l过定点P(5，0)．
当直线l不过圆心(即原点O)时，OM⊥AB，
∴ M在以线段OP为直径的圆上，以线段OP为直径的圆的方程为
(x－
)2＋y2＝
； (*)
当直线l过圆心(即原点O)时，O恰为弦AB的中点，O点的坐标满足的方程(*)．
∵ 弦AB中点在已知圆内，
∴弦AB中点的轨迹是以OP为直径的圆在已知圆内的部分，它的方程为
(x－)2＋y2＝(0≤x＜
)．
5．解 设动圆圆心M(x，y)，动圆的半径为r，点M到l1、l2的距离分别为d1、d2．
根据弦、弦心距、半径三者间关系，有
＋(
)2＝r2，
＋(
)2＝r2，
可得 ＋132＝＋122，
即 －＝52．
①
根据点到直线距离公式，得
d1＝
，d2＝
，
代入①式得
－
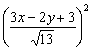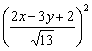＝52．
化简得(x＋1)2－y2＝65，这就是所求的轨迹方程．
6．解 如图27－5，设椭圆的左顶点为A(x，y)．
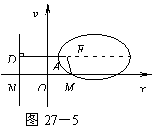作AD⊥l，为垂足．
∵ 
＝
＝.
从而 F(
，y)．
又MN＝3，∴ FM＝
.
∴ (
－1)2＋y2＝(
)2.
即椭圆左顶点的轨迹方程为 x2＋
＝1．
7．解法１ 如图27－6，由已知得F(1，0)，l：x＝－1．
设B(x0，y0)，则椭圆的半焦距为
c＝｜OF｜＝｜OO1｜－｜OF｜＝x0－1（x0＞1），
椭圆的半长轴为a＝｜BF｜＝
．
椭圆的短轴端点B到准线l的距离为｜BB1｜＝｜NO｜＋｜OO1｜＝x0＋1．
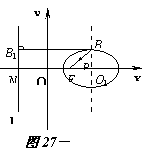由椭圆的定义，得
椭圆的离心率e＝
＝
,
又 e＝
＝
．
∴ ＝
，
化简得y02＝2(x0－1)（x0＞1）． ①
设线段BF的中点为P(x，y)，
∴
代入①式，化简得点P的轨迹方程为y2＝x－1（x＞1）．
解法2 设P(x，y)，则B(2x－1，y)．
∵ F(1，0)，l：x＝－1，
∴ ｜BB1｜＝(2x－1)＋1＝2x．
又 c＝(2x－1)－1＝2(x－1)（x＞1），
a2＝｜BF｜2＝(2x－2)2＋4y2.
由椭圆的定义，得
＝，即
＝，
∴ a2＝2cx． ②
将a2及c代入②式，并化简得P点之轨迹方程：
y2＝x－1（x＞1）．
解法3 设P(x，y)，则B(2x－1，2y)．
设x轴与准线l的交点为N，则｜FN｜＝2．
∵ ｜FN｜＝
－c＝
，
∴ ＝2，
即 b2＝2c． ③
∵ b＝｜2y｜，c＝2x－2（x＞1），代入③式得
y2＝x－1（x＞1）．
说明 (1)比较三种解法，可知代入法的关键在于能否建立合理的等式（如本题的等式①、②、③），再将等式转化为用动点坐标(x，y)来表示，即可求得动点的轨迹方程，与解法１相比，后两种解法中，几何元素a、b、c与动点坐标(x，y)之间的关系比较隐蔽，尽管书写表达比解法１简捷，但其解题思路远不如解法１来得直接明了．
(2)一般来说，能用代入法解的轨迹问题，也能用直接法解，因为二者没有本质的区别，不过代入法在揭示解题方向、目标上更为清晰．
8．解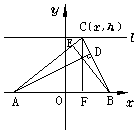
如图27－7. 设垂心为H(x，y)．
∵ A(－2，0)，B(2，0),l的方程为y＝3，
则 C点坐标为(x，3).
∵ BC⊥AD，
∴ kBC ·kAD＝－1，
即 
·
＝－1．化简得 x2＝4－3y．
图 27－7
9．解 由题知 a＝2，b＝1．
∴ A1(－2，0)、A2(2，0).
设P1(x1，y1)，则P2(x1，－y1)，
且 
＋y
＝1．
①
由于直线F1P1与F2P2的交点不可能落在坐标轴上，
∴ x1≠0，y1＞0．
设M(x，y)，则A1P1的方程为：
＝
， ②
A2P2的方程为：
＝
， ③
②×③得
＝
.
④
由①得
＝4．
⑤
将⑤代入④，得
－
＝1.
由y1＞0及②得 y≠0，
故M点的轨迹方程为－＝1（y≠0）.
10．解法1 ∵ a＝（x＋5）i＋yj，b＝（x－5）i＋yj，且｜a｜－｜b｜＝8．
∴ 点M（x，y）到两个定点F1（0，－5），F2（0，5）的距离之差为8．
∴ 轨迹C为以F1，F2为焦点的双曲线的右支，方程为
－
＝1（x≥4）．
解法2 由题知，
－
＝8，
移项，得 
＝8＋． ①
∴
＞．
解得 x＞0．
①两边平方，得 
＝
＋16＋64，
整理，得
4
＝5x－16，
两边平方，得 16[]＝（5x－16）2 (x≥
)，
展开，整理得 －＝1（x≥4）．
附录
例1．解法1 如图27－8，设P(x，y)是轨迹上任意一点．
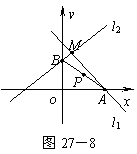∵ P为线段AB的中点，
∴ A（2x，0）、B(0，2y)．
①当两直线斜率存在时，kMA·kMB＝－1，
即 
·
＝－1(x≠)，
化简得x＋3y－5＝0(x≠)．
②若k1不存在，即A(1，0)，此时B(0，3)，AB中点为(，)，代入方程x＋3y－5＝0适合，即此点在直线x＋3y－5＝0上．
综合①、②，所求轨迹方程为x＋3y－5＝0，它表示一条直线．
解法2 设P(x，y)是轨迹上任意一点．
∵ P为线段AB的中点，AB为Rt△ABC与Rt△ABM公共的斜边，
∴ ｜OP｜＝｜MP｜．
∴ P(x，y)的轨迹是线段OM的垂直平分线．
说明 解法1是通过斜率的关系来列式的，所以要分k1存在与不存在两种情况(k2一定存在)来解题，结果②中所得点(，)恰好是①中直线上所缺的一个点；解法2是利用动点的几何性质来求的，是直接法的体现．往往，用动点的几何性质求轨迹方程比较简捷，在下面的学习中应好好体会．
另外，“轨迹”与“轨迹方程”是两个不同的概念，前者要指出曲线的形状、大小、位置，后者仅指方程．
例2．解 设M的坐标为(x，y)．
∵ 椭圆的两个焦点分别是F1(－2，0)，F2(2，0)，
∴ △MF1F2的重心G的坐标为(
，
)．
∵ G是椭圆上的点，
∴ 
，
即 
．
∵ M，F1，F2三点不共线，
∴ y≠0．
∴ M的轨迹方程是(y≠0)．
说明 本题采用的是转移法求轨迹方程，这是求轨迹方程的最基本方法，其基本特点是：利用动点的坐标表示参照点(或称之为相关点)的坐标，结合参照点的坐标满足已知曲线方程，从而间接得到动点的坐标满足的方程，即轨迹方程．
一般地，在一些问题中，动点P(x，y)随着另一动点Q(x1，y1)(参照点)而运动，如果参照点Q的运动规律易于揭示或Q点就在一已知曲线上运动，即满足约束条件f(x1，y1)＝0，这时，只要寻求P、Q两点坐标之间的关系，如
并将这种关系代入f(x1，y1)＝0，即可求得动点P的轨迹方程．方程f(x，y)＝0被称为动点P的轨迹方程的母方程．
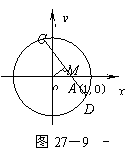例3．解法1 如图27－9，设过A的直线方程为y＝k(x－1)．
由 
消去y，得
(1＋k2)x2－2k2x＋k2－4＝0，
再设弦的端点C(x1，y1)，D(x2，y2)，线段CD的中点为M(x，y)，
则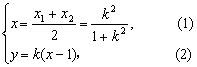 
当x≠1时，由(2)解得k＝
，代入(1)，整理得
x2＋y2－x＝0． ①
当k不存在，即CD⊥ox轴时，线段CD的中点就是A(1，0)点．
∵ A(1，0)在曲线①上，
∴方程①就是所求的轨迹方程．
解法2 ∵ OM⊥AM，
∴ 点M在以OA为直径的圆上．
∴ 线段OA中点(，0)是此圆的圆心，此圆的半径r＝．
又A点也是轨迹上的点．
∴ 线段CD的中点M的轨迹方程为(x－)2＋y2＝
．
说明 解法1是利用“参数法”，即用一个确定动点的量来表示动点的坐标(建立动点的坐标与这个参数之间的函数关系)，消去这个量(参数)，得到动点的坐标满足的方程；解法2是用动点的几何意义，利用已知的轨迹来求方程．两解法相比，优劣不言自明．因此在解有关圆的题目时，尽量运用它的几何性质，会给你的计算中带来便捷．
例4．解 (1)如图27－10，设M(x，y)．
由于MA⊥MB Û ｜MA｜2＋｜MB｜2＝｜AB｜2，
故(
)2＋(
)2＝(2a)2且y≠0． ①
化简得 x2＋y2＝a2（y≠0）．
②
也可以这样解：由于MA⊥MB Û kMA·kMB＝1，
即 
·
＝－1，
③
化简得 x2＋y2＝a2（x≠±a）. ④
(2) 设∠MAB＝a，∠MBA＝b，
∵ tanb＝tan2a， ⑤
由图26－10知，0≤a＋b≤p．
∵ b＝2a， ⑥
∴ 0≤a≤
，又x＞－a．
∴当y≥0时，tana＝kMA＝（x≠－a），
tanb＝tan(p－∠xBM)＝－kMB＝
（x≠a）．
由 tanb＝tan2a＝
，
即 ＝
，
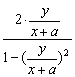⑦
整理得 y(3x2－y2＋2ax－a2)＝0． ⑧
当y＜0时，同样可得上式．
又x＝a时，tanb不存在，但b＝
，依题意，只要a＝
，M仍为所求的点．
∵ 1＝tan＝tana＝±＝±
，
∴ y＝±2a，
即点(a，±2a)在所求的轨迹上．
容易验证点(a，2a)与(a，－2a)的坐标都满足方程⑧，
故所求的轨迹方程为y＝0（－a＜x＜a）与3x2－y2＋2ax－a2＝0（x＞－a）.
说明 对b＝的情况进行验证是必要的，否则将破坏轨迹的完备性．
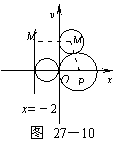例5．解 将已知圆的方程化为(x－2)2＋y2＝4．
这是圆心在P(2，0)，半径r＝2的一个圆(圆27－10 ).
当⊙M位于y轴右方时，作直线x＝－2．
依题意，点M到P点的距离等于它到直线x＝－2的距离．
由抛物线的定义，即得动点M的轨迹方程为
y2＝8x．
当⊙M位于y轴左方时，
依题意，⊙M只能与⊙P相切于O点，此时，⊙M的圆心M必落在x轴的负半轴上，
∴ M点的轨迹方程为y＝0（x＜0）．
∴ M点的轨迹方程为y2＝8x或y＝0（x＜0）．
说明 (1)本题没有直接运用距离公式，通过添作辅助线，创造了运用抛物线定义的条件，从而避免了繁杂的运算．可见在解题中要善于创造条件，充分运用圆锥曲线的定义以简化运算．
(2)在求动点的轨迹的问题中，要考虑各种可能出现的情况，如本题中若遗漏方程y＝0（x＜0），将破坏轨迹的完备性．
例6．解 设F(x，y)，则椭圆左焦点F′的坐标为
＝x－2c，
＝y.
∵
＝
，
∴ a2＝2c2．
又y轴为椭圆的左准线，
∴ x＝＋c＝3c．
∴
c＝．
∴ 左焦点F′的坐标为(x－
，y)，即F′(
，y)．
又由已知点M在椭圆上，
∴
＝．
即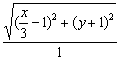 
＝．
∴ 椭圆右焦点F的轨迹方程为
＋2(y＋1)2＝1．
说明 通过本题，更能看出“转移法”在求轨迹方程过程中的重要作用．
由题知，a＝2，b＝1，得 c＝
．
∴ F1(－
，0)、F2(，0)．
设 P1(x1，y1)，则P2(x1，－y1)．
由题知， ＋y＝1（x1＞0）．
①
设M(x，y)，则
F1P1：
＝
，
②
F2P2：
＝
， ③
②÷③得
x1＝
，
代入②得
y1＝
．
将x1，y1代入①，得
4x2－12y2＝9．
由于直线F1P1与F2P2的交点只可能落在第一或第三象限，
故M点的轨迹方程为4x2－12y2＝9（xy＞0）．
说明 (1)在本题中，P＝{M｜M∈直线F1P1且M∈直线F2P2}，故M＝F1P1∩F2P2．由曲线与方程的定义，M点的坐标就是方程组②、③的解．由于点M的运动与动点P1相关，因而本题的技巧在于没有直接从方程组②、③中求x，y,而是求出了x1，y1，再利用代入法求得点M的轨迹方程，这种预见性在解题中常常可以达到减少思维回路、缩简运算程序的目的，值得引起重视．
(2)本题答案中条件“xy＞0”不可遗漏，否则将破坏轨迹的纯粹性．
例8．解 设P(x，y)．∵ M(－1，0)，N(1，0)，
∴ MP＝(x＋1，y)，PM＝(－x－1，－y)，MN＝(2，0)，
NM＝(－2，0)，PN＝(1－x，y)，NP＝(x－1，－y)，
∴ MP·MN＝2(x＋1)，PM·PN＝x2＋y2－1，NM·NP＝2(1－x)．
∵ MP·MN，PM·PN，NM·NP成等差数列，且公差为负数，
∴ 
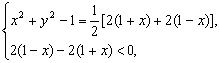
即 
＝3(x＞0)．
∴ 这就是点P的轨迹方程，轨迹是以原点为圆心，为半径的圆在y轴右边的部分(半圆不含端点)．
说明 这是2002年全国高考(新课程卷)的一道解答题，是以向量为背景的轨迹题，充分体现了向量的工具性作用，这一点在求轨迹方程时应好好体会．一般来说，求曲线(轨迹)方程式，如果实际到两直线的夹角、两直线互相垂直等知识，应考虑是否能利用向量知识来解，既方便，又简捷．
分析：考虑到P1，P2是椭圆上两个关于x轴对称的点，点M同时在直线F1P1与F2P2上，可利用点M的坐标同时满足直线F1P1，F2P2的方程，消去有关参照量，建立M的轨迹方程．
例8．已知平面内两点M(－1，0)，N(1，0)，若动点P满足MP·MN，PM·PN，NM·NP成等差数列，且公差为负数，求点P的轨迹方程．
分析：将向量的数量积用P的坐标x，y表示，结合三个数成等差数列的等价条件，建立关于x，y的方程，就是P的轨迹方程．