高三春期入学考试数学试题
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.设集合![]() ,则集合
,则集合![]() 的子集的个数是: A.11 B.10 C.15 D.16
的子集的个数是: A.11 B.10 C.15 D.16
2.已知![]() : A.
: A.![]() B.8 C.18 D.
B.8 C.18 D. ![]()
3.函数![]() ,则函数
,则函数![]() 在点
在点![]() 处的变化率是:
处的变化率是:
A.2 B.-2 C.4 D.-4
4.奇函数![]() 满足
满足![]() ,则
,则![]() :
:
A.11 B.-11 C.2 D.-2
5.一班有学员54人,二班有学员42人,现在要用分层抽样的方法从两个班抽出一部分人
参加4×4方队进行军训表演,则一班和二班分别被抽取的人数是:
A.9人、7人 B.15人、1人 C.8人、8人 D.12人、4人
6.函数f(x)=log2(x-1) + log2(x+2)的反函数是g(x),则g(2)等于:
A.2 B.1 C.-3 D.2 或-3
7.一个学生通过某种英语听力测试的概率是1/2,他连续测试n次,要保证他至少有一次通过的的概率大于0.9,那么他测试的次数n的最小值为:
A.3 B.4 C.5 D.6
8.已知函数![]() ,则函数
,则函数![]() 的最大值是:
的最大值是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.数列![]() ,则该数列相邻两项的积是负数的是:
,则该数列相邻两项的积是负数的是:
A.![]() B.a22·a23 C.a23·a24 D.a24·a25
B.a22·a23 C.a23·a24 D.a24·a25
10.甲乙两人同时从相距72英里的M,N出发且相向而行,甲以每小时4英里的速度步行,
乙第1小时步行2英里,第2小时步行2.5英里,第3小时步行3英里等等(成等差数
列),经过t小时甲乙相遇A点.则一定有:
A.![]() B.
B.![]() C.
C.![]() D.以上都不对
D.以上都不对
11.已知椭圆![]() 和抛物线
和抛物线![]() 的离
的离
心率分别为e1、e2、e3,则:
A.e1e2< e3 B.e1e2= e3 C.e1e2> e3 D.e1e2≥e3
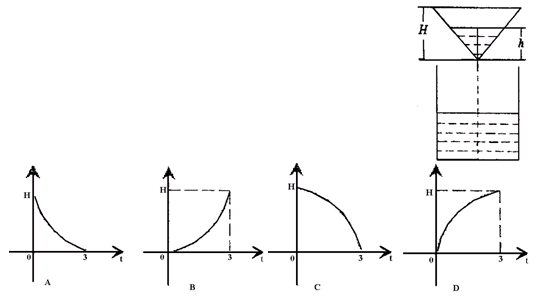 12.如图,液体从一个圆锥形漏斗漏入一圆柱桶中,开始时漏
12.如图,液体从一个圆锥形漏斗漏入一圆柱桶中,开始时漏
斗盛满液体,经过3秒漏完,圆柱桶中液面上升速度是一
个常量,则漏斗中液面的高度![]() 与下落时间
与下落时间![]() 的函数关系
的函数关系
的图像只可能是:
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分. 把答案填在题中的横线上.
13.二项式![]() 的展开式中的第六项是63,而第三项的二项式系
的展开式中的第六项是63,而第三项的二项式系
数是21,则![]() .
.
14.在某次数学测验中,学号为![]() 的四位同学的考试成绩
的四位同学的考试成绩![]()
且满足![]() ,则四位同学的考试成绩的所有可能情况有
,则四位同学的考试成绩的所有可能情况有
种(用数字作答).
15.不等式![]() 的解集为
.
的解集为
.
16.关于函数![]() ,有下列命题:
,有下列命题:
①![]() 的图象可由函数
的图象可由函数![]() 的图象向左平移
的图象向左平移![]() 个单位得到.
个单位得到.
②![]() 的图象可由函数
的图象可由函数![]() 的图象向左平移
的图象向左平移![]() 个单位得到.
个单位得到.
③![]() 的图象关于点
的图象关于点![]() 对称.
对称.
④![]() 的表达式可改写成
的表达式可改写成![]() .
.
其中正确命题的序号是 .
春期入学考试
答 题 卷
一、选择题答题框(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题(每小题4分,共16分)
13、 ; 14、 ;
15、 ; 16、_____ ___ 。
三、解答题:本大题共6小题,共74分. 解答应写出文字说明、证明过程或推演步骤.
17.(本小题满分12分)
已知集合![]() ,集合
,集合![]() .
.
(1)若A的区间长度为3,试求t的值.
(2)某个函数![]() 的值域是B,且
的值域是B,且![]() ∈A的概率不小于0.6,试确定t的取值范围.
∈A的概率不小于0.6,试确定t的取值范围.
18.(本小题满分12分)
已知函数![]() ,
,![]() (
(![]() 为正常数),且函数
为正常数),且函数![]() 与
与![]() 的图象在
的图象在![]() 轴上的截距相等。
轴上的截距相等。
(1)求![]() 的值; (2)求函数
的值; (2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)若![]() 为正整数,证明:
为正整数,证明:![]() .
.
19.(本小题满分12分)
平面向量![]() ,点M为直线OP上的一个动点.
,点M为直线OP上的一个动点.
(1)当![]() 取最小值,求
取最小值,求![]() 的坐标;
的坐标;
(2)当点M满足(1)的条件和结论时,求![]() 的余弦值.
的余弦值.
20.(本小题满分12分)
某厂使用两种零件A、B装配两种产品P、Q,该厂的生产能力是月产P产品最多有2500
件,月产Q产品最多有1200件;而且组装一件P产品要4个A零件、2个B零件,组
装一件Q产品要6个A零件、8个B零件,该厂在某个月能用的A零件最多14000个;
B零件最多12000个. 已知P产品每件利润1000元,Q产品每件利润2000元,欲使月
利润最大,需要组装P、Q产品各多少件?最大利润多少万元?
21.(本小题满分12分)
已知A、B、C是直线m上的三点,且AB=BC=6,⊙O′切直线m于点A,又过B、C
作⊙O′异于![]() 的两切线,切点分别为D、E,设两切线交于点P,
的两切线,切点分别为D、E,设两切线交于点P,
(1)求点P的轨迹方程
(2)经过点C的直线![]() 与点P的轨迹交于M、N两点,且点C分
与点P的轨迹交于M、N两点,且点C分![]() 所成比等于2∶3,
所成比等于2∶3,
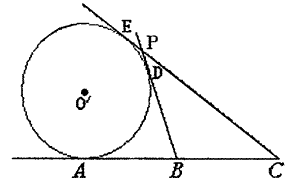 求直线
求直线![]() 的方程.
的方程.
22.(本上题满分14分)
设二次函数![]() ,若
,若![]() 且
且![]() .
.
(1)试证:![]() ;
;
(2)试比较![]() 与
与![]() 之间的大小关系;
之间的大小关系;
(3)试比较![]() 与
与![]() 之间的大小关系.
之间的大小关系.
参考答案
一、选择题:D D C B A A B D C C A C
二、填空题:13.![]() 14.15 15.{xkπ-
14.15 15.{xkπ-![]() ≤x≤kπ+
≤x≤kπ+![]() , k∈Z} 16.②③④
, k∈Z} 16.②③④
三、解答题:17.(1)![]() ………5分
………5分
(2)![]() . 即
. 即![]() …12分
…12分
18.(1)由题意,![]() ,
,![]() 又
又![]() ,所以
,所以![]() ………3分
………3分
(2)![]() ………5分
………5分
当![]() 时,
时,![]() ,它在
,它在![]() 上单调递增;………6分
上单调递增;………6分
当![]() 时,
时,![]() ,它在
,它在![]() 上单调递增。………7分
上单调递增。………7分
(3)设![]() ,对于数列
,对于数列![]() ,解不等式
,解不等式![]() ,由
,由![]() ,上式化为
,上式化为![]() ,解得
,解得![]() ………9分。因
………9分。因![]() 得
得![]() ,于是
,于是![]() ,而
,而![]() 所以
所以![]() 。………12分
。………12分
19.解:(1)设M(x,y),∵点M在OP上,故![]() 共线,又
共线,又![]() ,
,
即x=2y ![]() ,
,
![]() ,
,
于是![]() ,……6分
,……6分
即当且仅当![]() 时,
时,![]() 取得最小值-8,此时
取得最小值-8,此时![]() .……8分
.……8分
(2)当![]() 时,有
时,有![]() ,…9分
,…9分
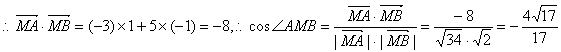 20.解:设分别生产P、Q产品x件、y件,则有……1分
20.解:设分别生产P、Q产品x件、y件,则有……1分
![]() ……4分
……4分
设利润![]() ,要使利润S最大,只需求
,要使利润S最大,只需求![]() 的最大值. …6分
的最大值. …6分 ![]()
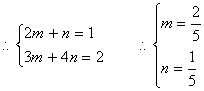
有![]() .
.
当且仅当![]() 时,取等号,……10分
时,取等号,……10分
此时最大利润![]() .……12分
.……12分
21.(1)![]()
![]()
![]() 点轨迹是B,C为焦点,长轴长等于18的椭圆. ……3分
点轨迹是B,C为焦点,长轴长等于18的椭圆. ……3分
以B,C两点所在直线为x轴,线段BC的垂直平分线为y轴建立直角坐标系.
则可设椭圆的方程是![]()
![]()
![]() 点的轨迹方程是
点的轨迹方程是![]() ……6分
……6分
(2)设![]() ,
,
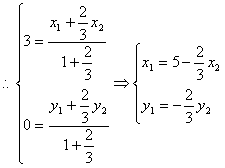 ……8分
……8分
![]() ①
①
又![]() ② 由①、②消去
② 由①、②消去![]()
解得![]() ……10分
……10分
∴由C、N可得直线的方程是:![]() ……12分
……12分
22.(1)![]()
![]()
![]() ……………2分
……………2分
![]() ………………………4分
………………………4分
(2)令![]() ,则
,则![]() ………………6分
………………6分
∴![]()
![]() =
=
![]() (由于
(由于![]() )。所以
)。所以![]() ……9分
……9分
(3)又由已知:![]()
![]()
![]() ……………………………12分,
……………………………12分,
因此 当a>0时,![]()
当a<0时,![]() …………14分
…………14分