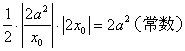高三第二轮复习导数专题训练3
一．选择题
1．设f(x)=cosx,则
（A）sinα (B)-sinα (C)cosα (D)-cosα
2．设
等于
3．抛物线y=
在横坐标为x=4的点处的切线方程为
（A）4x-y-18=0 (B)x+4y+4=0 (C)x-4y+4=0 (D)4x+y-18=0
4．等边三角形的高为8时，面积对高的变化率为
5．一物体的运动方程为
，则物体在t=2时的速度为
6．
则a的值为
7．已知函数
是
（A）奇函数 （B）偶函数 （C）非奇非偶函数 （D）既是奇函数也是偶函数
8．设f(x)在x处可导，则
等于
9．函数
10．若f(x)=sina-cosx，则
（A）2sina (B)sina (C)cosa (D)sina+cosa
11.f(x)与g(x)是定义在R上的两个可导函数，则
的
（A）充分不必要条件（B）必要不充分条件 （C）充要条件 （D）既不充分也不必要条件
12．已知
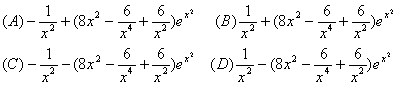
二．填空题
13．函数
的导数是
14．函数
的导数是 。
15．已知抛物线
在点（1,2）处与直线y=x+1相切，则b-c=
.
16．已知函数
。
三．解答题
17．求函数
的导数
18．试求经过原点且与曲线
相切的切线方程
19．设曲线
在它们交点处的两切线的夹角为α，求tanα
20．已知函数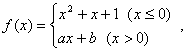
若f(x)在x=0处可导，求a,b的值
21＊．求证：双曲线
在任一点处的切线与两坐标轴构成的三角形面积等于常数
答案：一、ABCDD ABCCB BA；二、13、
三．17、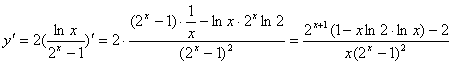
18．设切点为
①∴
设所求的切线方程为 y=kx 则
②又k=
③由①②③解得
易得切点为
，故所求的切线方程为x+y=0或x+25y=0
19．由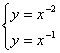
，解得两曲线的交点为（1,1）。设两曲线在交点处的切线斜率分别为
，则
由两直线的夹角公式得tanα=
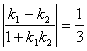
20．
若b≠1，则
不存在∴b=1,又∵f(x)在x=0处可导∴a=1
21．设
上任一点，
∴曲线在
处的切线方程为
，令x=0，求得切线在y轴上的切距为
，故切线与y轴的交点为
，令y=0得切线与x轴的交点为
∴切线与两坐标轴围成的三角形面积等于
