高考数学普通高等学校春季招生考试
数学试题（安徽卷）
（理工农医类）
第Ⅰ卷（选择题，共60分）
一、选择题：本大题共12小题，每小题5分，共60分
在每小题给出的四个选项中，只有一项是符合题目要求的.
1.在
轴和
轴上的截距分别为
，3的直线方程是（ ）
A.
B.
C.
D.
2.集合
包含
的
的子集共有（ ）
A.2个 B.3个 C.5个 D.8个
3.圆
截轴所得的弦与截轴所得的弦的长度之比为( )
A. 
B.
C. 
D.
4.下列函数中,周期为
,图像关于直线
对称的函数是( )
A.
B. 
C. 
D.
5.不等式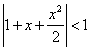
的解集是( )
A.
B. 
C. 
D.
6.已知
,则等于( )
A.
B. 
C. 
D.
7.
( )
A.
B. 
C.
D.6
8.已知斜三棱柱的长为
,两个侧面面积分别为
,且这两侧面所成的角为
,那么,这个棱柱的体积为( )
A.
B. 
C. 
D. 
9.某校刊设有9门文化课专栏,由甲,乙,丙三位同学每人负责3个专栏,其中数学专栏由甲负责,则不同的分工方法有( )
A.1680种 B.560种 C.280种 D.140种
10.一个二面角的大小为
,其棱为
,正三角形
和正三角形
分别在二面角的两个面上,则
( )
A.
B. 
C.
D.
11.等差数列
中,若
,前
项和
,则
( )
A.7 B.9 C.17 D.19
12.设函数
表示除以3的余数,对
都有( )
A.
B. 
C.
D.
请将选择题答案填入下面表格内
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
第Ⅱ卷（非选择题，共90分）
二.填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上
13.若复数
满足
,则=
14.
的展开式中常数项为
(用数字作答)
15.椭圆
在第一象限部分的一点
,以点横坐标作为长轴长,纵坐标作为短轴长作椭圆
,如果的离心率等于
的离心率,则的坐标为
16.一个半径为
的实心钢球放在倒圆锥形
的容器中(轴截面如图),再往容器中注水,使水
面恰好淹没钢球,如果容器轴截面的顶角为,
那么,将球取出后,水面的高度为
三.解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
已知
18. (本小题满分12分)
已知双曲线经过点
,渐近线方程是
,求其焦点坐标和离心率.
19. (本小题满分12分)
如图,设三棱锥
各侧面与底面所成
的角都相等,且
.
(1)
证明:
(2)
若
,
求
与底面所成的角.
20. (本小题满分12分)
设
,且
,定义在区间
内的函数
是奇函数.
(1)
求
的取值范围;
(2)
讨论函数
的单调性.
21. (本小题满分12分)
已知抛物线
关于直线
对称.
(1)
求
(2)
求
焦点间距离.
22. (本小题满分14分)
设
的根,且
,令
.
(1)
求
;
(2)
证明:
;
(3)
证明:
.