高考数学普通高等学校招生全国统一考试2
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页,第Ⅱ卷3至9页。共150分。考试时间120分钟。
第Ⅰ卷(选择题 共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦
干净后,再选涂其它答案。不能答在试题卷上。
3.考试结束,监考人将本试卷和答题卡一并交回。
|
三角函数的积化和差公式
![]()
![]()
![]()
![]()
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只
有一项是符合题目要求的.
1.满足条件M∪{1}={1,2,3}的集合M的个数是
A.1 B.2 C.3 D.4
2.在平面直角坐标系中,已知两点![]() 则AB的值是
则AB的值是
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
3.下列四个函数中,以π为最小正周期,且在区间(![]() )上为减函数的是
)上为减函数的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.64个直径都为![]() 的球,记它们的体积之和为V甲,表面积之和为S甲;一个直径为a的球,
的球,记它们的体积之和为V甲,表面积之和为S甲;一个直径为a的球,
记其体积为V乙,表面积为S乙,则
A.V甲>V乙且S甲>S乙 B.V甲<V乙且S甲<S乙
C.V甲=V乙且S甲>S乙 D.V甲=V乙且S甲=S乙
5.已知某曲线的参数方程是![]() 为参数).若以原点为极点,x轴的正半轴为极轴,
为参数).若以原点为极点,x轴的正半轴为极轴,
长度单位不变,建立极坐标系,则该曲线的极坐标方程是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.给定四条曲线:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .其中与直
.其中与直
线![]() 仅有一个交点的曲线是
仅有一个交点的曲线是
A.①②③ B.②③④ C.①②④ D.①③④
7.已知![]() 且z1=1.若
且z1=1.若![]() ,则
,则![]() 的最大值是
的最大值是
A.6 B.5 C.4 D.3
8.若![]() ,则
,则![]() 的值为
的值为
A.3 B.-3 C.-2 D.![]()
9.12名同学分别到三个不同的路口进行车流量的调查,若每个路口4人,则不同的分配方
案共有
A.![]() 种 B.
种 B.![]() 种 C.
种 C.![]() 种 D.
种 D.![]() 种
种
10.设命题甲:“直四棱柱ABCD—A1B1C1D1中,平面ACB1与对角面BB1D1D垂直”;命题
乙:“直四棱柱ABCD—A1B1C1D1是正方体”.那么,甲是乙的
A.充分必要条件 B.充分非必要条件
C.必要非充分条件 D.既非充分又非必要条件
|
么不等式![]() 的解集是
的解集是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
![]()
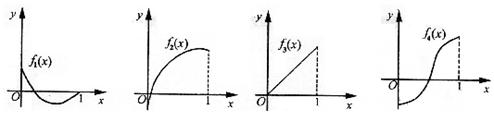
12.如图所示,![]() 是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]
是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]
中任意的x1和x2,任意![]() 恒成立”的只有
恒成立”的只有
|
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共90分)
注意事项:
1.第Ⅱ卷共7页,用钢笔或圆珠笔直接答在试题卷中。
2.答卷前将密封线内的项目填写清楚。
| 题 号 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 分 数 | ||||||||

二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横
线上.
13.![]() 从小到大的顺序是
.
从小到大的顺序是
.
14.等差数列{an}中,a1=2,公差不为零,且a1,a3,a11恰好是某等比数列的前三项,那么
该等比数列公比的值等于 .
15.关于直角AOB在定平面α内的射影有如下判断:①可能是0°的角;②可能是锐角;③
可能是直角;④可能是钝角;⑤可能是180°的角.其中正确判断的序号是
(注:把你认为是正确判断的序号都填上).
16.已知P是直线![]() 上的动点,PA,PB是圆
上的动点,PA,PB是圆![]() 的两
的两
条切线,A,B是切点,C是圆心,那么四边形PACB面积的最小值为 .
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
 |
17.(本小题满分12分)
解不等式![]() .
.
 18.(本小题满分12分)
18.(本小题满分12分)
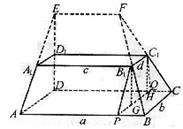
如图,在多面体ABCD—A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E,F两点,上、下底面矩形的长、宽分别为c,d与a,b且a>c,b>d,两底面间的距离为h..
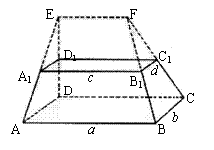 (Ⅰ)求侧面ABB1A1与底面ABCD所成二面角的大小;
(Ⅰ)求侧面ABB1A1与底面ABCD所成二面角的大小;
(Ⅱ)证明:EF//面ABCD
(Ⅲ)在估测该多面体的体积时,经常运用近似公式
V估=S中截面·h来计算.已知它的体积公式是
![]() (S上底面+4S中截面+S下底面),
(S上底面+4S中截面+S下底面),
试判断V估与V的大小关系,并加以证明.
(注:与两个底面平行,且到两个底面距离相等的截面称为该多面体的中截面.)

19.(本小题满分12分)
数列{xn}由下列条件确定:![]()
(Ⅰ)证明:对n≥2,总有![]() ;
;
(Ⅱ)证明:对n≥2,总有![]() ;
;
(Ⅲ)若数列{xn}的极限存在,且大于零,求![]() 的值.
的值.
 |
20.(本小题满分12分)
在研究并行计算的基本算法时,有以下简单模型问题:
用计算机求n个不同的数![]() 的和
的和![]() .计算开始前,n个数存贮在n台由网络连接的计算机中,每台机器存一个数,计算开始后,在一个单位时间内,每台机器至多到一台其他机器中读数据,并与自己原有数据相加得到新的数据,各台机器可同时完成上述工作.
.计算开始前,n个数存贮在n台由网络连接的计算机中,每台机器存一个数,计算开始后,在一个单位时间内,每台机器至多到一台其他机器中读数据,并与自己原有数据相加得到新的数据,各台机器可同时完成上述工作.
为了用尽可能少的单位时间,使各台机器都得到这n个数的和,需要设计一种读和加的方法.比如n=2时,一个单位时间即可完成计算,方法可用下表表示:
| 机器号 | 初始时 | 第一单位时间 | 第二单位时间 | 第三单位时间 | |||
| 被读机号 | 结 果 | 被读机号 | 结 果 | 被读机号 | 结 果 | ||
| 1 | v1 | 2 | v1+ v2 | ||||
| 2 | v2 | 1 | v2+v1 | ||||
(Ⅰ)当n=4时,至少需要多少个单位时间可完成计算?
把你设计的方法填入下表
| 机器号 | 初始时 | 第一单位时间 | 第二单位时间 | 第三单位时间 | |||
| 被读机号 | 结 果 | 被读机号 | 结 果 | 被读机号 | 结 果 | ||
| 1 | v1 | ||||||
| 2 | v2 | ||||||
| 3 | v3 |
| |||||
| 4 | v4 |
| |||||
(Ⅱ)当n=128时,要使所有机器都得到![]() ,至少需要多少个单位时间可完成计算?(结论不要求证明)
,至少需要多少个单位时间可完成计算?(结论不要求证明)

21.(本小题满分13分)
已知O(0,0),B(1,0),C(b,c)是△OBC的三个顶点.
(Ⅰ)写出△OBC的重心G,外心F,垂心H的坐标,并证明G,F,H三点共线;
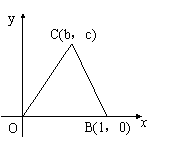 (Ⅱ)当直线FH与OB平行时,求顶点C的轨迹.
(Ⅱ)当直线FH与OB平行时,求顶点C的轨迹.
 |
22.(本小题满分13分)
已知![]() 是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足:
是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足:
![]() .
.
(Ⅰ)求f(0),f(1)的值;
(Ⅱ)判断![]() 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(Ⅲ)若![]() ,求数列{un}的前n项的和Sn.
,求数列{un}的前n项的和Sn.
数学试题(理工农医类)(北京卷)参考解答
说明:
一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.
二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.
四、只给整数分数.选择题和填空题不给中间分.
一、选择题:本题考查基本知识和基本运算.每小题5分,满分60分.
1.B 2.D 3.B 4.C 5.D 6.D 7.C 8.A 9.A 10.C 11.B 12.A
二、填空题:本题考查基本知识和基本运算.每小题4分,满分16分.
13.![]() 14.4 15.①②③④⑤ 16.
14.4 15.①②③④⑤ 16.![]()
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
17.本小题主要考查不等式的解法等基本知识,考查运算能力和逻辑思维能力.满分12分.
解:原不等式![]() 因为
因为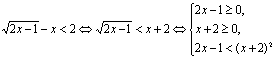
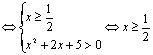 又
又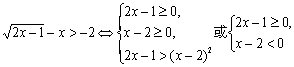
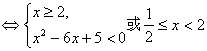
![]()
![]() .所以,原不等式组的解集为
.所以,原不等式组的解集为![]() .
.
18.本小题主要考查直线、平面的位置关系,考查不等式的基本知识,考查空间想象能力和
|
(1)解:过B1C1作底面ABCD的垂直平面,交底面于
PQ,过B1作B1G⊥PQ,垂足为G.∵平面ABCD∥平
面A1B1C1D1,∠A1B1C1=90°,∴AB⊥PQ,AB⊥
B1P. ∴∠B1PG为所求二面角的平面角.过C1作
C1H⊥PQ,垂足为H.由于相对侧面与底面所成二
面角的大小相等,故四边形B1PQC1为等腰梯形.
∴![]() ,
,![]()
![]()
即所求二面角的大小为![]()
(Ⅱ)证明:∵AB,CD是矩形ABCD的一组对边,有AB//CD,又CD是面ABCD与
面CDEF的交线, ∴AB//面CDEF. ∵EF是面ABFE与面CDEF的交线,∴AB
∥EF. ∵AB是平面ABCD内的一条直线,EF在平面ABCD外,∴EF∥面ABCD.
(Ⅲ)V估<V.证明:
∵a>c,b>d,∴![]()
![]() ∴V估<V.
∴V估<V.
19.本小题主要考查数列、数列极限、不等式等基本知识,考查逻辑思维能力. 满分12分.
(Ⅰ)证明:由![]() ,可归纳证明
,可归纳证明![]() (没有证明过程不扣分).
(没有证明过程不扣分).
从而有![]() ,所以,当n≥2时,
,所以,当n≥2时,![]() 成立.
成立.
(Ⅱ)证法一:当n≥2时,因为![]() ,所以
,所以
![]() ,故当n≥2时,
,故当n≥2时,![]() 成立.
成立.
证法二:当n≥2时,因为![]() ,所以
,所以
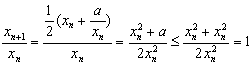 ,故当n≥2时,
,故当n≥2时,![]() 成立.
成立.
(Ⅲ)解:记![]() 得
得
![]() ,
,
故![]()
20.本小题主要考查运用数学思想方法,分析和解决科学问题的能力.满分12分.
(Ⅰ)解:当n=4时,只用2个单位时间即可完成计算.
方法之一如下:
| 机器号 | 初始时 | 第一单位时间 | 第二单位时间 | 第三单位时间 | |||
| 被读机号 | 结 果 | 被读机号 | 结 果 | 被读机号 | 结 果 | ||
| 1 | v1 | 2 | v1+ v2 | 3 | v1+ v2+ v3+ v4 | ||
| 2 | v2 | 1 | v2+v1 | 4 | v2+ v1+ v4+ v3 | ||
| 3 | v3 | 4 | v3+ v4 | 1 | v3+ v4+ v1+ v2 | ||
| 4 | v4 | 3 | v4+ v3 | 2 | v4+ v3+ v2+ v1 | ||
(Ⅱ)解:当n=128=27时,至少需要7个单位时间才能完成计算.
21.本小题主要考查直线与椭圆等基本知识,考查分析问题和解决问题的能力. 满分13分.
(Ⅰ)解:由△OBC三顶点坐标O(0,0),B(1,0),C(b,c)(c≠0),可求得
重心![]() ,外心F
,外心F![]() ,垂心
,垂心![]() .当
.当![]() 时,
时,
G,F,H三点的横坐标均为![]() ,故三点共线;当
,故三点共线;当![]() 时,设G,H所在直线的斜
时,设G,H所在直线的斜
率为![]() ,F,G所在直线的斜率为
,F,G所在直线的斜率为![]() .因为
.因为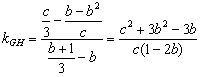 ,
,
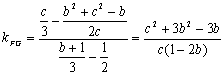 ,所以
,所以![]() ,G,F,H三点共线.
,G,F,H三点共线.
综上可得,G,F,H三点共线.
(Ⅱ)解:若FH//OB,由![]() ,得
,得![]() ,
,
配方得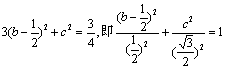 ,即
,即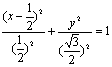
![]() .
.
所以,顶点C的轨迹是中心在(![]() ,0),长半轴长为
,0),长半轴长为![]() ,短半轴长为
,短半轴长为![]() ,且短
,且短
轴在x轴上的椭圆,除去(0,0),(1,0),(![]() ,
,![]() ),(
),(![]() ,-
,-![]() )四点.
)四点.
22.本小题主要考查函数与数列等基本知识,考查分析问题和解决问题的能力. 满分13分.
(Ⅰ)解:![]() . 因为
. 因为![]() ,
,
所以![]()
(Ⅱ)![]() 是奇函数. 证明:因为
是奇函数. 证明:因为![]() ,
,
![]() 因此,
因此,![]() 为奇函数.
为奇函数.
(Ⅲ)解法一:由![]() ,
,
猜测![]() . 下面用数学归纳法证明:
. 下面用数学归纳法证明:
1° 当n=1时,![]() ,公式成立;
,公式成立;
2°假设当n=k时,![]() 成立,那么当n=k+1时,
成立,那么当n=k+1时,
![]() ,公式仍成立.
,公式仍成立.
由上两步可知,对任意![]() 成立.所以
成立.所以![]() .
.
因为![]() 所以
所以![]() ,
,
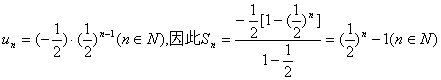 .
.
解法二:当![]() ,
,
故![]()
所以![]() (以下同解法一)
(以下同解法一)