高考数学普通高等学校招生全国统一考试6
数 学(文史类)
第Ⅰ卷(选择题 共60分)
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B) S=4πR2
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是P. ![]()
那么n次独立重复试验中恰好发生k次的概
率 其中R表示球的半径
![]()
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.不等式![]() 的解集是 ( )
的解集是 ( )
A.(0,2) B.(2,+∞)
C.(2,4) D.(-∞,0)∪(2,+∞)
2.抛物线y=ax2 的准线方程是y=2,则a的值为 ( )
A.![]() B.-
B.-![]() C.8 D.-8
C.8 D.-8
3.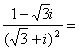 ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 已知![]() ( )
( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
5.等差数列![]() ( )
( )
A.48 B.49 C.50 D.51
6.双曲线虚轴的一个端点为M,两个焦点为F1,F2,∠F1MF2=120°,则双曲线的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.设函数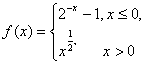 若
若![]() ,则x0的取值范围是 ( )
,则x0的取值范围是 ( )
A.(-1,1) B.(-1,+∞)
C.(-∞,-2)∪(0,+∞) D.(-∞,-1)∪(1,+∞)
8.O是平面上一 定点,A、B、C是平面上不共线的三个点,动点P满足
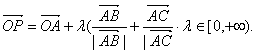 则P的轨迹一定通过△ABC的 ( )
则P的轨迹一定通过△ABC的 ( )
A.外心 B.内心 C.重心 D.垂心
9.函数![]() 的反函数为 ( )
的反函数为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.棱长为a的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1).一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后,依次反射到CD、DA和AB上的点P2,P3和P4(入射角等于反射角)。若P4与P0重合,则tanθ= ( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
12.一个四面体的所有棱长都为![]() ,四个顶点在同一球面上,则此球的表面积为 ( )
,四个顶点在同一球面上,则此球的表面积为 ( )
A.3π B.4π C.![]() D.6π
D.6π
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.答案填在题中横线上.
13.![]() 展开式中
展开式中![]() 的系数是
.
的系数是
.
14.某公司生产三种型号的轿车,产量分别为1200辆,6000辆和2000辆,为检验该公司的
产品质量。现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车依次应抽取
, , 辆。
15.在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC2.”拓展到空间,类比平面几何的勾股定理,研究三棱锥的面面积与底面面积间的关系。可以得出的正确结论是:“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直,则 ”。
|
作物且相邻的试验田不能种植同一作物,不同的种植
方法共有 种.(以数字答)
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
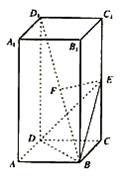
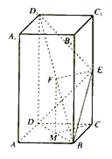
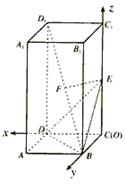
已知正四棱柱ABCD—A1B1C1D1.AB=1,AA1=2,点E为CC1中点,点P为BD1中点.
|
(2)求点D1到面BDE的距离.
18.(本小题满分12分)
已知抛物线C1:y=x2+2x和C:y=-x2+a,如果直线l同时是C1和C2的切线,称l是C1和C2的公切线,公切线上两个切点之间的线段,称为公切线段.
(Ⅰ)a取什么值时,C1和C2有且仅有一条公切线?写出此公切线的方程;
(Ⅱ)若C1和C2有两条公切线,证明相应的两条公切线段互相平分.
19.(本题满分12分)
已知数列![]()
(Ⅰ)求![]()
(Ⅱ)证明![]()
20.(本小题满分12分)
在三种产品,合格率分别是0.90,0.95和0.95,各抽取一件进行检验.
(Ⅰ)求恰有一件不合格的概率;
(Ⅱ)求至少有两件不合格的概率. (精确到0.001)
21.(本小题满分12分)
已知函数![]() 是R上的偶函数,其图象关于点
是R上的偶函数,其图象关于点
![]() 对称,且在区间
对称,且在区间![]() 上是单调函数.求
上是单调函数.求![]() 的值.
的值.
22.(本小题满分14分)
已知常数a>0,向量c=(0,a),i=(1,0),经过原点O以c+λi为方向向量的直线与经过定点A(0,a)以i-2λc为方向向量的直线相交于点P,其中λ∈R.试问:是否存在两个定点E、F,使得PE+PF为定值.若存在,求出E、F的坐标;若不存在,说明理由.
普通高等学校招生全国统一考试6参考解答
一、选择题:本题考查基本知识和基本运算。每小题5分,满分60分。
1.C 2.B 3.B 4.D 5.C 6.B 7.D 8.B 9.B 10.C 11.C 12.A
二、填空题:本题考查基本知识和基本运算,每小题4分,满分16分。
13.![]() 14.6,30,10 15.S2△ABC+ S2△ACD +
S2△ADB = S2△BCD 16.42
14.6,30,10 15.S2△ABC+ S2△ACD +
S2△ADB = S2△BCD 16.42
三、解答题
|
(1)证法一:取BD中点M.连结MC,FM .
∵F为BD1中点 , ∴FM∥D1D且FM=![]() D1D .
D1D .
又EC![]() CC1且EC⊥MC ,∴四边形EFMC是矩形
CC1且EC⊥MC ,∴四边形EFMC是矩形
∴EF⊥CC1. 又CM⊥面DBD1 .∴EF⊥面DBD1 .
∵BD1![]() 面DBD1 . ∴EF⊥BD1
. 故EF为BD1
与CC1的公垂线.
面DBD1 . ∴EF⊥BD1
. 故EF为BD1
与CC1的公垂线.
证法二:建立如图的坐标系,得
B(0,1,0),D1(1,0,2),F(![]() ,
,![]() ,1),C1(0,0,2),E(0,0,1).
,1),C1(0,0,2),E(0,0,1).
|
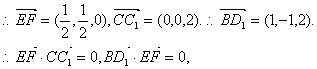
即EF⊥CC1,EF⊥BD1 . 故EF是为BD1 与CC1的公垂线.
(Ⅱ)解:连结ED1,有VE-DBD1=VD1-DBE .
由(Ⅰ)知EF⊥面DBD1 ,设点D1到面BDE的距离为d.
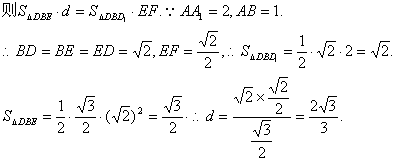
故点D1到平面DBE的距离为![]() .
.
18.本小题主要考查导数、切线等知识及综合运用数学知识解决问题的能力,满分12分。
(Ⅰ)解:函数y=x2+2x的导数y′=2x+2,曲线C1在点P(x1,x![]() +2x1)的切线方程是:
+2x1)的切线方程是:
y-(x![]() +2x1)=(2x1+2)(x-x1),即 y=(2x1+2)x-x
+2x1)=(2x1+2)(x-x1),即 y=(2x1+2)x-x![]() ①
①
函数y=-x2+a的导数y′=-2x, 曲线C2 在点Q(x2,-x![]() +a)的切线方程是
+a)的切线方程是
即y-(-x![]() +a)=-2x2(x-x2). y=-2x2x+x
+a)=-2x2(x-x2). y=-2x2x+x![]() +a .
②
+a .
②
如果直线l是过P和Q的公切线,则①式和②式都是l的方程,
![]() x1+1=-x2
x1+1=-x2
所以
- x![]() =x
=x![]() +a.
+a.
消去x2得方程 2x![]() +2x2+1+a=0.
+2x2+1+a=0.
若判别式△=4-4×2(1+a)=0时,即a=-![]() 时解得x1=-
时解得x1=-![]() ,此时点P与Q重合.
,此时点P与Q重合.
即当a=-![]() 时C1和C2有且仅有一条公切线,由①得公切线方程为 y=x-
时C1和C2有且仅有一条公切线,由①得公切线方程为 y=x-![]() .
.
(Ⅱ)证明:由(Ⅰ)可知.当a<-![]() 时C1和C2有两条公切线
时C1和C2有两条公切线
设一条公切线上切点为:P(x1,y1), Q(x2 , y2 ).
其中P在C1上,Q在C2上,则有
x1+x2=-1,
y1+y2=x![]() +2x1+(-x
+2x1+(-x![]() +a)= x
+a)= x![]() +2x1-(x1+1)2+a=-1+a .
+2x1-(x1+1)2+a=-1+a .
线段PQ的中点为![]()
同理,另一条公切线段P′Q′的中点也是![]()
所以公切线段PQ和P′Q′互相平分.
19.本小题考查数列,等比数列,等比数列求和等基础知识,考查运算能力,满分12分.
(Ⅰ)∵a1=1 . ∴a2=3+1=4, a3=32+4=13 .
(Ⅱ)证明:由已知an-an-1=3n-1,故
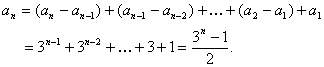
所以证得![]() .
.
20.本小题主要考查相互独立事件概率的计算,运用数学知识解决问题的能力,满分12分.
解:设三种产品各抽取一件,抽到合格产品的事件分别为A、B和C.
(Ⅰ)P(A)=0.90,P(B)=P(C)=0.95.
P![]() =0.10 , P
=0.10 , P![]() =P
=P![]() =0.05.
=0.05.
因为事件A,B,C相互独立,恰有一件不合格的概率为
P(A·B·![]() )+P(A·
)+P(A·![]() ·C)+P(
·C)+P(![]() ·B·C)
·B·C)
=P(A)·P(B)·P(![]() )+P(A)·P(
)+P(A)·P(![]() )·P(C)+P(
)·P(C)+P(![]() )·P(B)·P(C)
)·P(B)·P(C)
=2×0.90×0.95×0.05+0.10×0.95×0.95
=0.176
答:恰有一件不合格的概率为0.176.
(Ⅱ)解法一:至少有两件不合格的概率为
P(A·![]() ·
·![]() )+P(
)+P(![]() ·B·
·B·![]() )+P(
)+P(![]() ·
·![]() ·C)+ P(
·C)+ P(![]() ·
·![]() ·
·![]() )
)
=0.90×0.052+2×0.10×0.05×0.95+0.10×0.052
=0.012.
答:至少有两件不合格的概率为0.012.
解法二:三件产品都合格的概率为
P(A·B·C)=P(A)·P(B)·P(C)
=0.90×0.952
=0.812.
由(Ⅰ)知,恰有一件不合格的概率为0.176,所以至少有两件不合格的概率为
1-P(A·B·C)+0.176
=1-(0.812+0.176)
=0.012
答:至少有两件不合格的概率为0.012.
21.本小题主要考查三角函数的图象和单调性,奇偶性等基本知识,以及分析问题和推理计算能力,满分12分.
解:由f(x)是偶函数,得f(-x)= f(-x).
即: ![]() 所以-
所以-![]()
对任意x都成立,且![]() 所以得
所以得![]() =0.
=0.
依题设0![]() ,所以解得
,所以解得![]() ,
,
由f(x)的图象关于点M对称,得![]() .
.
取x=0,得![]() =-
=-![]() ,所以
,所以![]() =0.
=0.

22.本小题主要考查平面向量的概念和计算,求轨迹的方法,椭圆的方程和性质,利用方程判定曲线的性质,曲线与方程的关系等解析几何的基本思想和综合解题能力,满分14分。
解:根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在两定点,使得点P到两定点距离的和为定值.
∵i=(1,0),c=(0,a), ∴![]()
因此,直线OP和AP的方程分别为 ![]() y=ax和y-a=-2
y=ax和y-a=-2![]() ax .
ax .
消去参数![]() ,得点P(x,y)的坐标满足方程y (y-a)=-2a2x2
,
,得点P(x,y)的坐标满足方程y (y-a)=-2a2x2
,
整理得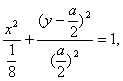 ①
①
因为a>0,所以得:
(i)当a=![]() 时,方程①是圆方程,故不存在合乎题意的定点E和F;
时,方程①是圆方程,故不存在合乎题意的定点E和F;
(ii)当0<a<![]() 时,方程①表示椭圆,焦点E
时,方程①表示椭圆,焦点E![]() 和
和
![]() 为合乎题意的两个定点;
为合乎题意的两个定点;
(iii)当a>![]() 时,方程①表示椭圆,焦点E
时,方程①表示椭圆,焦点E![]() 和F
和F![]() ))为合乎题意的两个定点.
))为合乎题意的两个定点.