高考数学模拟试题2
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,第I卷1至2页(第1至12题),第II卷3至8页(第13至22题)共150分,考试时间120分钟。
第I卷(选择题共60分)
注意事项:
1、答第I卷前,考生务必将本人的学校、班级、姓名、考试号填在第II卷的密封线内。
2、将第I卷上每小题所选答案前的字母标号填写在第II卷卷首相应的答题栏内,在第I卷上答题无效。
3、考试结束,只交第II卷。
一、选择题(本大题共12个小题;每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合A、B,则 ![]() =A是A
=A是A![]() B=B的
B=B的
(A)充分而不必要的条件 (B)必要而不充分的条件 (C)充要条件 (D)既不充分,也不必要的条件
2.函数y=2x+1的反函数的图象大致是
函数y=2x+1的反函数的图象大致是
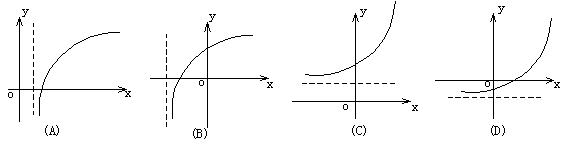
3.等比数列{an}中,a1+a2=40,
a3+a4=60,则a5+a6等于
(A)120 (B)100 (C)90 (D)80
4.对于函数y=sin4x+cos4x,有
(A)周期是π,值域是[0,1] (B)周期是 ![]() ,值域是[
,值域是[ ![]() ,1]
,1]
(C)周期是 ![]() ,值域是[
,值域是[ ![]() ,1] (D)周期是
,1] (D)周期是 ![]() ,值域是[0,1]
,值域是[0,1]
5.如果抛物线y2=a(x+1)的准线方程是x=-3,则这条抛物线的焦点坐标是
(A) (3,0) (B) (2,0) (C) (1,0) (D) (-1,0)
6.极坐标系中,方程 ![]() =2sinθ表示的曲线是
=2sinθ表示的曲线是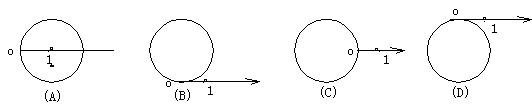
7.记二项式(1+2x)n展开式的各项系数和为an,各项的二项式系数和为bn,则 ![]()
(A) -1 (B) 1 (C) 0 (D)不存在
8.复数z的一个三次方根是-1+3i,若arg(-1+3i)=a,则z的另两个三次方根的辐角主值的和是
(A)a+2π (B)2a+2π (C)2a+ ![]() (D)2a+
(D)2a+ ![]()
9.圆x2+y2=3内横坐标与纵标均为整数的点共有9个,以这些点为顶点的三角形的个数有
(A) 84个 (B)81个 (C)78个 (D)76个
10.长方体的全面积为72,则长方体的对角线的最小值是
(A)6 ![]() (B)3
(B)3 ![]() (C)3 (D)6
(C)3 (D)6
11.已知函数f1(x)=x, f2(x)=
![]() ,f3(x)=4-x,函数g(x)取f1(x)、f2(x)、f3(x)中的最小值,则函数g(x)的最大值是
,f3(x)=4-x,函数g(x)取f1(x)、f2(x)、f3(x)中的最小值,则函数g(x)的最大值是
(A) 2 (B) 1 (C) ![]() (D)不存在
(D)不存在
12.如果一个四面体的三个面都 是直角三角形,则第四个面不可能是
(A)直角三角形 (B)锐角三角形 (C)钝角三角形 (D)等腰三角形
二、填空题(本大题共4小题;每小题4分,共16分,把答案填在题中的横线上)
13.设复数z满足条件z=z-1+i,则z的最小值是 。
14.如果圆x2+y2=1与圆(x-3)2+y2=r2相切,则半径r的值为 。
15.如果一个圆锥中有三条母线两两所成的角均为600,那么这个圆锥侧面展开图的圆心角等于 。
16.某产品今后四年的市场年需求量依次构成数列{an}(n=1,2,3,4),并预测到年需求量第二年比第一年增长的百分率为p1,第三年比第二年增长的百分率为p2,第四年比第三年增长的分率为p3,且p1+p2+p3=1,给出如下数值:① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④ ![]() ;⑤
;⑤ ![]() ,则其中可能为这四年间市场需求量的平均增长率的是 。(要求:把可能的数值的序号都填上)
,则其中可能为这四年间市场需求量的平均增长率的是 。(要求:把可能的数值的序号都填上)
三、解答题(本大题共6小题;共74分,解答题应写出证明过程或演算步骤。)
17、(本小题8满分12分)
![]() ABC中,a、b、c分别为角A、B、C的对边,已知
ABC中,a、b、c分别为角A、B、C的对边,已知 ![]() ,又
,又 ![]() ABC的面积为
ABC的面积为 ![]() ,且a+b=11,求角C及边C。
,且a+b=11,求角C及边C。
| 得分 | 评卷人 |
18、(本小题满分12分)
已知数列1,3,6……的各项由一个等比数列{an}与一个首项为0的等差数列{bn}的对应项相加而得到。
(I)求这个数列的前n的项和Sn;
(II)设 ![]() 的值。
的值。
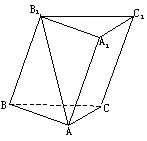
| 19、(本小题满分12分) (II)求AB1与平面BB1C1C所成角的正切值; (III)在平面AA1B1B内找一点P,使三棱锥P-BB1C为正三棱锥,并求P到平面BB1C距离。 |
|
20、(本小题满分12分)
据某市旅游局预测:从明年初开始的前x个月内,外地游客到该市旅游的总人数f(x)(万人)与月份x的近似关系为:
![]()
(I)写出明年第x个月到该市旅游的外地游客人数g(x)(万人)与月份x的关系式;
(II)该市现在每日只能接待游客1500人,接照预测计算,明年是否要增加接待能力?(第月按30天计算)
21、(本小题满分12分)
已知又曲线 ![]() 在左右顶点分别是A,B,点P是其右准线上的一点,若点A关于点P的对称点是M,点P关于点B的对称点是N,且M、N都在此双曲线上。
在左右顶点分别是A,B,点P是其右准线上的一点,若点A关于点P的对称点是M,点P关于点B的对称点是N,且M、N都在此双曲线上。
(I)求此双曲线的方程;
(II)求直线MN的倾斜角。
22.(本小题满分14分)
定义在(-1,1)上的函数f(x)满足:对任意x、y ![]() (-1,1)都有
(-1,1)都有 ![]() 。
。
(I)求证:函数f(x)是奇函数;
(II)如果当 ![]() 时,有f(x)>0,判断f(x)在(-1,1)上的单调性,并加以证明;
时,有f(x)>0,判断f(x)在(-1,1)上的单调性,并加以证明;
(III)设-1<a<1,解不等式: ![]()
答案及评分标准1
一、选择题(每小题5分,共60分)
1.C
2.A
3.C
4.B
5.C
6.B
7.A
8.B
9.D
10.D 11.B 12.C
二、填空题(每小题4分,共16分)
13. ![]() 14.2或4
15.
14.2或4
15. ![]() 16.①或③
16.①或③
三、解答题
17.解:由 ![]() ,得
,得
![]()
∴ ![]()
又∵A+B+C=
![]() ∴
∴
![]() 5’
5’
由 ![]() ,得ab=24 7’
,得ab=24 7’
c2=a2+b2-2abcosC=a2+b2-ab=(a+b)2-3ab=112-3
![]() =49
=49
c=7 12’
18.(I)设等比数列的公比为q,等差数列的公差在d,则
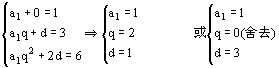 4’
4’
∴ ![]() 6’
6’
(II) ![]() 8’
8’
![]() 12’
12’
19.(I)证:因为平面BB1C1C ![]() 平面ABC。
平面ABC。
平面BB1C1C
![]() 平面ABC=BC
平面ABC=BC
AC ![]() BC
BC
![]() 平面BB1C1C 3’
平面BB1C1C 3’
(II)取BB1中点M,连AM、CM、CB1
∵BC=BB1, ![]() ∴
∴ ![]() 是等边三角形
是等边三角形
∴B1C=BC=2
∴CM ![]()
∵AC
![]() 平面BB1C1C
∴BB1
平面BB1C1C
∴BB1 ![]() MA
MA
∴ ![]() 为二面角A—B1B—C的平面角 5’
为二面角A—B1B—C的平面角 5’
∴ ![]() Rt
Rt
![]() 中,AC=1
中,AC=1
由AC![]() 平面BB1C1C
知
平面BB1C1C
知 ![]() AB1C为直线AB1与平面BB1C1C所成的角
AB1C为直线AB1与平面BB1C1C所成的角
![]() 7’
7’
(III)在AM上取点P,使AP=2PM,则P点为所求
在CM上取点O,使CO=2OM,连PO
2’
则PO//AC,且PO=
![]()
![]() 平面BB1C
平面BB1C ![]() 平面BB1C
平面BB1C
且 ![]() BB1C为等边三角形 ∴三棱锥P—BB1C为正三棱锥
BB1C为等边三角形 ∴三棱锥P—BB1C为正三棱锥
且P到平面BB1C的距离为PO,PO=
![]() 12’
12’
20.(I)当x=1时,g(1)=f(1)= ![]() 2’
2’
当 ![]() ,g(x)=f(x)-f(x-1)
,g(x)=f(x)-f(x-1)
![]()
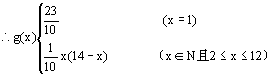 6’
6’
(II)当 ![]()
![]() 9’
9’
![]()
![]()
∴明年需增加接待能力。 12’
21.(I)点A、B的坐标为A(-3,0),B(3,0),设点P、M、N的坐标依次为
![]()
则有 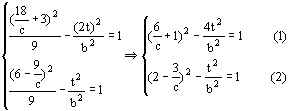 3’
3’
② ![]() 4-①得
4-①得 ![]() ,解得c=5
,解得c=5
故所求方程是 ![]() 6’
6’
(II)由②得, ![]() 9’
9’
所以,M、N的坐标为 ![]()
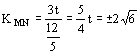
所以MN的倾斜角是 ![]() 12’
12’
22.(I)证:令x=y=0,则f(0)+f(0)=f(0),
故f(0)=0令y=-x,则f(x)+f(-x)=![]()
∴f(-x)=-f(x)
∴函数f(x)的奇函数 4’
(II)设-1<x1<x2<1,则 ![]()
![]()
![]()
因此![]()
![]()
∴函数f(x)在(-1,1)上是减函数 8’
(III)![]() 是(-1,1)上的减函数,
是(-1,1)上的减函数,
![]()
由![]() 得x<0或x>2 9’
得x<0或x>2 9’
当a=0时,![]() ,原不等式的解集为{xx>2} 10’
,原不等式的解集为{xx>2} 10’
当-1<a<0时。x>2中原不等式的解;
若x<0,则a(x-1)>1,x<1+ ![]()
故原不等式的解集为![]() 12’
12’
当0<a<1时,x<0不是原不等式的解;
若x>2,则a(x-1)<1,x<1+ ![]()
∴ ![]()
故原不等式的解集为{x ![]() } 14’
} 14’