高考数学模拟试题8
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共124分，考试时间80分钟.
第Ⅰ卷（选择题，共60分）
一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有
一项是符合题目要求的.
1．设集合
，则集合
的子集
的个数是 （ ）
A．11 B．10 C．15 D．16
2．已知
（ ）
A．
B．8 C．18 D．
3．函数
，则函数
在点
处的变化率是 （ ）
A．2 B．－2 C．4 D．－4
4．奇函数
满足
，则
（ ）
A．11 B．－11 C．2 D．－2
5.（文科）一班有学员54人，二班有学员42人，现在要用分层抽样的方法从两个班抽出一部分人 参加4×4方队进行军训表演，则一班和二班分别被抽取的人数是 （ ）
A．9人、7人 B．15人、1人 C．8人、8人 D．12人、4人
5.(理科)随机变量ξ的概率分布规律为
其中a是常数，则
的值为 （
）
A．
B．
C．
D．
6．已知A，B，C是△ABC的三个内角，且
，则角C的大小是（ ）
A．
B．
C．
D．
7．
等于 （ ）
A．－１ B． C．0 D．∞
8．已知函数
，则函数的最大值是 （ ）
A．
B．
C．
D．
9．函数
的值域是 （ ）
A．
B．
C．
D．
10．甲乙两人同时从相距72英里的M，N出发且相向而行，甲以每小时4英里的速度步行，
乙第1小时步行2英里，第2小时步行2.5英里，第3小时步行3英里等等（成等差数
列），经过t小时甲乙相遇A点.则一定有 （ ）
A．
B．
C．
D．以上都不对
|
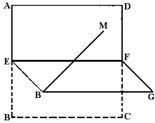
将正方形沿EF折成直二面角（如图），M为矩形AEFD内一
点如果
MB和平面BCF所成角的正切值为
，那么点M到直线EF的距离为
（ ）
|
B．1 C．
D．
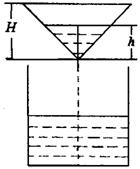
12．如图，液体从一个圆锥形漏斗漏入一圆柱桶中，开始时漏
斗盛满液体，经过3秒漏完，圆柱桶中液面上升速度是一
个常量，则漏斗中液面的高度
与下落时间
的函数关系
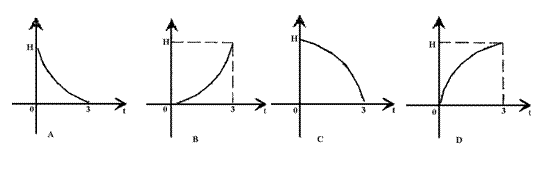的图像只可能是
（
）
二、填空题：本大题共4小题，每小题4分，共16分. 把答案填在题中的横线上.
13．二项式
的展开式中的第六项是63，而第三项的二项式系
数是21，则
.
14．在某次数学测验中，学号为
的四位同学的考试成绩
且满足
，则四位同学的考试成绩的所有可能情况有
种（用数字作答）.
15．关于函数
，有下列命题：
①
的图象可由函数
的图象向左平移个单位得到.
②的图象可由函数的图象向左平移个单位得到.
③的图象关于点
对称.
④的表达式可改写成
.
其中正确命题的序号是 .
16．对于每个正整数n，抛物线
与x轴交于An，Bn两点，以
表示该两点的距离，则
=
.
三、解答题：本大题共3小题，共48分. 解答应写出文字说明、证明过程或推演步骤.
17．（本小题满分12分）
已知集合
，集合
.
（1）若A的区间长度为3，试求t的值.
（2）某个函数的值域是B，且∈A的概率不小于0.6，试确定t的取值范围.
18．（本小题满分12分）设
有唯一解，
（1）问数列
是否是等差数列？
（2）求
的值.
19．（本小题满分12分）
平面向量
，点M为直线OP上的一个动点.
（1）当
取最小值，求
的坐标；
（2）当点M满足（1）的条件和结论时，求
的余弦值.
20．（本小题满分12分）
某厂使用两种零件A、B装配两种产品P、Q，该厂的生产能力是月产P产品最多有2500
件，月产Q产品最多有1200件；而且组装一件P产品要4个A零件、2个B零件，组
装一件Q产品要6个A零件、8个B零件，该厂在某个月能用的A零件最多14000个；
B零件最多12000个. 已知P产品每件利润1000元，Q产品每件利润2000元，欲使月
利润最大，需要组装P、Q产品各多少件？最大利润多少万元？
高考数学模拟试题8参考答案
一、选择题
DDCBA（D） DBDAB CC
二、填空题
13． 14．15
15．②③④ 16．1
16．略解：因为
，所以，
三、解答题
17．（1）
（2）
.
即
18．（1）由
，所以由题知
.
又因为
. 所以数列是首项为1002，公差等于
的等差数列.
（2）由（1）知
19．解：（1）
点M在OP上，故
共线，又
，
即x=2y
，
，
于是
，
即当且仅当
时，取得最小值－8，此时
.
（2）当时，有
，
.
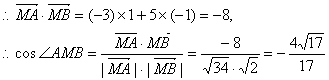20．解：设分别生产P、Q产品x件、y件，则有
设利润
要使利润S最大，只需求
的最大值.
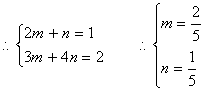
有
.
当且仅当
时，取等号，
此时最大利润