数学奥林匹克高中训练题(12)
第一试
一、选择题(每小题6分,共36分)
1.(训练题17)方程![]() 所对应的曲线图形是(D)
所对应的曲线图形是(D)
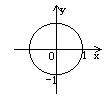
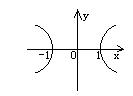
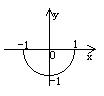
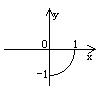
(A) (B) (C) (D)
2.(训练题17)在数列![]() 中,
中,![]() 且当
且当![]() ≥1时,
≥1时,![]() 等于
等于![]() 的个位数字。则
的个位数字。则![]() 等于(B)
等于(B)
(A)2 (B)4 (C)6 (D)8
3.(训练题17)已知四边形![]() 的四边长
的四边长![]() 满足
满足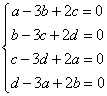 ,则四边形
,则四边形![]() 一定是(D)
一定是(D)
(A)梯形 (B)圆内接四边形 (C)矩形 (D)菱形
4.(训练题17)如果![]() 的展开式中含常数项,则正整数
的展开式中含常数项,则正整数![]() 的最小值是(B)
的最小值是(B)
(A)4 (B)5 (C)6 (D)8
5.(训练题17)已知![]() 表示不超过
表示不超过![]() 的最大整数,
的最大整数,![]() ,
,![]() ,记
,记![]()
![]()
![]() ,则
,则![]() 的值为(B)
的值为(B)
(A)3 (B)4 (C)5 (D)6
6.(训练题17)如果关于![]() 的方程,
的方程,![]() 至少有一个模等于1的根,那么实数
至少有一个模等于1的根,那么实数![]() 的值(C)
的值(C)
(A)不存在 (B)有一个 (C)有三个 (D)有四个
二、填空题(每小题9分,共54分)
1.(训练题17)求值![]()
![]() 。
。
2.(训练题17)已知函数![]()
![]() ≤
≤![]() ≤
≤![]() 和
和![]() 的图象围成一个封闭的平面图形。则这个图形的面积是
4
。
的图象围成一个封闭的平面图形。则这个图形的面积是
4
。
3.(训练题17)实数![]() 满足
满足![]() ,设
,设![]() . 则
. 则![]() -5 。
-5 。
4.(训练题17)已知![]() 的面积
的面积![]() 与内角
与内角![]() 均为定值.则
均为定值.则![]() 边的长
边的长![]() 的取值范围是
的取值范围是![]() .
.
5.(训练题17)设由模为1的![]() (2<
(2<![]() <6)个复数满足下面2条组成一个集合
<6)个复数满足下面2条组成一个集合![]() .
.
(1)![]() ;
;
(2)若![]() 则
则![]() ,其中
,其中![]() =
=![]() .
.
则集合![]() =
=
![]() .
.
6.(训练题17)今有壹角币1张,贰角币1张,伍角币1张,壹元币5张,伍元币2张。则可以付出不同数目的款额(不包括不付款的情况)的种数是 127 .
第二试
一、(训练题17)(满分25分)已知![]()
求证:![]() ≤1
≤1
二、(训练题17)(满分25分)设点P是双曲线C:![]() 1(
1(![]() >0,
>0,![]() >0)上任意一点,过点
>0)上任意一点,过点![]() 的直线与两渐进线
的直线与两渐进线![]() :
:![]() ,
,![]() :
:![]() 分别交于点
分别交于点![]() ,设
,设![]() =
=![]() .
.
求证:![]()
![]() =
=![]()
![]()
三、(训练题17)(满分35分)在△![]() 的边
的边![]() 上任取一点
上任取一点![]() ,过
,过![]() 作
作![]() 的平行线交
的平行线交![]() 于
于![]() ,过
,过![]() 作
作![]() 的平行线交
的平行线交![]() 于
于![]() ,是否存在
,是否存在![]() 点以外的一个定点
点以外的一个定点![]() ,使得
,使得![]() 四点共圆?证明你的结论。
四点共圆?证明你的结论。
四、(训练题17)(满分35分)在公差![]() >0的正项等差数列
>0的正项等差数列![]() :
:![]() …,
…,![]() 中,任取
中,任取![]() 个数。试证明其中必存在两个数
个数。试证明其中必存在两个数![]() 满足不等式
满足不等式
1<![]() <2.
<2.