抽样方法、正态分布 复习指导
重点、难点讲解:
1.抽样的三种方法:简单随机抽样、系统抽样、分层抽样。后两种方法是建立在第一种
方法基础上的。三种方法的异同比较见课本P22表。
2.了解如何用样本估计总体: 用样本估计总体的主要方法是用样本的频率分布来估计总体分布,主要有总体中的个体取不同数值很少和较多甚至无限两种情况。
3.正态曲线及其性质:正态分布常记作N(![]() ),其正态分布函数:f(x)=
),其正态分布函数:f(x)= 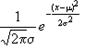 ,
x∈(-∞,+∞)。 把N(0,1)称为标准正态分布,相应的函数表达式:f(x)=
,
x∈(-∞,+∞)。 把N(0,1)称为标准正态分布,相应的函数表达式:f(x)= ![]() ,
x∈(-∞,+∞)。
,
x∈(-∞,+∞)。
正态图象的性质: ①曲线在x轴的上方,与x轴不相交。
②曲线关于直线x=μ对称。 ③曲线在x=μ时位于最高点。
④当x<μ时,曲线上升;当x>μ时,曲线下降,并且当曲线向左、右两边无限
延伸时,以x轴为渐近线,向它无限靠近。
⑤当μ一定时,曲线的形状由σ确定,σ越大,曲线越“矮胖”,表示总体的
分布越分散;σ越小,曲线越“瘦高”,表示总体的分布越集中。
4.一般正态分布与标准正态分布的转化
对于标准正态分布,用![]() 表示总体取值小于x0的概率,即
表示总体取值小于x0的概率,即![]() =p(x<x0),其几何意义是由正态曲线N(0,1),x轴,直线x=x0所围成的面积。又根据N(0,1)曲线关于y轴的对称性知,
=p(x<x0),其几何意义是由正态曲线N(0,1),x轴,直线x=x0所围成的面积。又根据N(0,1)曲线关于y轴的对称性知,![]() ,并且标准正态总体在任一区间(a,b)内取值概率
,并且标准正态总体在任一区间(a,b)内取值概率![]() 。
任一正态总体N(
。
任一正态总体N(![]() ),其取值小于x的概率F(x)=
),其取值小于x的概率F(x)= ![]() 。
。
知识应用举例:

例2.为了了解某大学一年级新生英语学习的情况,从503名大学一年级学生中抽取50名作为样本,如何采用系统抽样方法完成这一抽样?
思路分析:因为总体的个数503,样本的容量50,不能整除,故可采用随机抽样的方法从总体中剔除3个个体,使剩下的个体数500能被样本容量50整除,再用系统抽样方法。
解:第一步:将503名学生随机编号1,2,3,……,503
第二步:用抽签法或随机数表法,剔除3个个体,剩下500名学生,然后对这500名学生重新编号。
第三步:确定分段间隔k=![]() =10,将总体分成50个部分,每部分包括10个个体,第一部分的个体编号为1,2,……,10;第二部分的个体编号11,12,……,20;依此类推,第50部分的个体编号491,492,……,500。
=10,将总体分成50个部分,每部分包括10个个体,第一部分的个体编号为1,2,……,10;第二部分的个体编号11,12,……,20;依此类推,第50部分的个体编号491,492,……,500。
第四步:在第一部分用简单随机抽样确定起始的个体编号,例如是7。
第五步:依次在第二部分,第三部分,……,第五十部分,取出号码为17,27,……, 497,这样就得到了一个容量为50的样本。
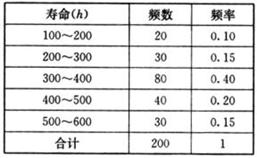
例4.对某电子元件进行寿命追踪调查,情况如下:

(1)列出频率分布表; (2)画出频率分布直方图;
(3)估计电子元件寿命在100h~400h以内的概率;
(4)估计电子元件寿命在400h以上的概率;
(5)估计总体的数学期望。
思路分析:由于样本的取得具有代表性,因此,可以利用样本的期望近似地估计总体的期望。
解:(1)样本频率分布表如下:
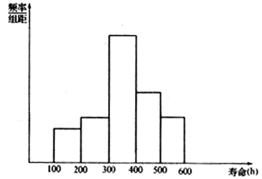
(2)频率分布直方图如下:
(3)从频率分布表可知,寿命在100h~400h的元件出现的概率为0.65;
(4)由频率分布表可知,寿命在400h以上的电子元件出现的频率为0.20+0.15=0.35,故我们估计电子元件寿命在400h以上的概率为0.35。
(5)样本的期望为:
![]()
![]()
所以,我们估计生产的电子元件寿命的总体期望值(总体均值)为365h。
例5.正态总体为μ=0, σ=1时的概率密度函数是f(x)= 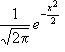 ,
x∈(-∞, +∞) ,
,
x∈(-∞, +∞) ,
(1)证明f(x)是偶函数;(2)利用指数函数的性质说明f(x)的增减性。
证明:(1)任意的x∈R,f(-x)= ![]() ,
∴f(x)是偶函数。
,
∴f(x)是偶函数。
(2)任取x1<x2<0,则![]() ,
,
∴![]() , ∴
, ∴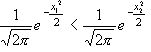 ,即f(x1)<f(x2)。
,即f(x1)<f(x2)。
这说明f(x)在(-∞,0)上是递增函数, 同理可证f(x)在(0, +∞)上是递减函数。
例6.随机变量ξ服从N(0,1),求下列值。
(1)P(ξ≥2.55) (2)P(ξ<-1.44) (3)P(ξ<1.52)
思路分析:标准正态分布,可以借助标准正态分布表。用到的公式主要有:Φ(-x)=1-Φ(x); P(a<x<b)=Φ(b)-Φ(a);p(x≥x0)=1-p(x<x0)。
解:(1)P(ξ≥2.55)=1-p(ξ<2.55)=1-Φ(2.55)=1-0.9946=0.0054。
(2)P(ξ<-1.44)=Φ(-1.44)=1-Φ(1.44)=1-0.9251=0.0749。
(3)P(ξ<1.52)=p(-1.52<ξ<1.52)=Φ(1.52)-Φ(-1.52)
=2Φ(1.52)-1=2×0.9357-1=0.8714。
例7.设![]() ,且总体密度曲线的函数表达式为:f(x)
,且总体密度曲线的函数表达式为:f(x) ![]() ,
x∈(-∞,+∞)。
,
x∈(-∞,+∞)。
(1)求μ,σ;(2)求p(x-1<![]() )及p(1-
)及p(1-![]() <x<1+
<x<1+![]() )。
)。
思路分析:对照正态曲线函数,可以得出μ,σ;利用一般正态总体N(![]() )与标准正态总体N(0,1)概率间的转化关系,可以求出(2)。
)与标准正态总体N(0,1)概率间的转化关系,可以求出(2)。
解:(1)整理得:f(x)= ![]() ,所以,μ=1, σ
,所以,μ=1, σ![]() ,故
,故![]() 。
。
(2)p(x-1<![]() )=p(1-
)=p(1-![]() <x<1+
<x<1+![]() )=F(1+
)=F(1+![]() )-F(1-
)-F(1-![]() )=Φ(
)=Φ(![]() )-Φ(
)-Φ(![]() )
)
=Φ(1)-Φ(-1)=2Φ(1)-1
=2×0.8413-1=0.6826。
p(1-![]() <x<1+2
<x<1+2![]() )=F(1+2
)=F(1+2![]() )-F(1-
)-F(1-![]() )=Φ(
)=Φ(![]() )-Φ(
)-Φ(![]() )
)
=Φ(2)-Φ(-1)=Φ(2)+Φ(1)-1
=0.9772+0.8413-1=0.8185。
例8.某城市从南郊某地乘车前往北区火车站有两条路可走,第一条线路穿过市区,路程较短,但交通拥挤,所需时间(单位:分钟)服从正态分布N(50,100), 第二条线路沿环城公路走,路程较长,但交通阻塞少,所需时间(单位:分钟)服从正态分布N(60, 16),(1)若只有70分钟时间可用,应走哪条路?
(2)若只有65分钟时间可用,应走哪条路?
思路分析:所谓最佳线路(应选择的线路)就是在允许的时间内有较大概率赶到火车站的那条线路。
解:设x为行车时间。
(1)走第一条路及时赶到的概率为:
P(0<x≤70)= ![]() ≈
≈![]() =Φ(2)=0.9772。
=Φ(2)=0.9772。
走第二条线路及时赶到的概率为:P(0<x≤70)=Φ(![]() )=Φ(2.5)=0.9938。
)=Φ(2.5)=0.9938。
因此应走第二条线路。
(2)走第一条线路及时赶到的概率为:
P(0<x≤65)≈Φ(![]() )=Φ
)=Φ![]() (1.5)=0.9332。
(1.5)=0.9332。
走第二条线路及时赶到的概率为:
P(0<x≤65)≈Φ(![]() )=Φ(1.25)=0.8944。
)=Φ(1.25)=0.8944。
因此应走第一条线路。