导数单元测试题
一、 选择题:
1、设在[0,1]上函数f(x)的图象是连续的,且![]() >0,则下列关系一定成立的是( )
>0,则下列关系一定成立的是( )
(A)f(0)<0(B)f(1)>0(C)f(1)>f(0)(D)f(1)<f(0)
2、函数y=1+3x-x3有 ( )
(A)极小值-1,极大值1(B)极小值-2,极大值3
(C)极小值-2,极大值2(D)极小值-1,极大值3
3、已知函数f(x)的导数为![]() ,且图象过点(0,-5),当函数f(x)取得极大值-5时,x的值应为( )
,且图象过点(0,-5),当函数f(x)取得极大值-5时,x的值应为( )
(A)-1 (B)0 (C)1 (D)±1
4、曲线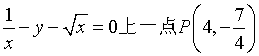 处的切线方程是(
)
处的切线方程是(
)
(A)5x+16y+8=0 (B)5x-16y+8=0
(C)5x+16y-8=0 (D)5x-16y-8=0
5、设a>0, f(x)=ax2+bx+c,曲线y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为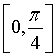 ,则P到曲线y=f(x)对称轴距离的取值范围为( )(A)
,则P到曲线y=f(x)对称轴距离的取值范围为( )(A)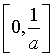 (B)
(B)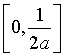 (C)
(C)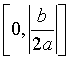 (D)
(D)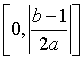
6、已知抛物线C1:y=x2+2x和C2:y=-x2+a,如果直线l同时是C1和C2的切线,称l是C1和C2的公切线,若C1和C2有且仅有一条公切线,则a的值为( )
(A)1 (B)-1 (C)![]() (D)
(D)![]()
二、 填空题:
7、函数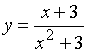 在点x=3处的导数为
。
在点x=3处的导数为
。
8、某质点的运动方程是S=t3-(2t-1)2,则在t=1s时的瞬时速度为 。
9、找一个非零函数f(x),使![]() 可以为
。
可以为
。
10、f(x)=x2+ax+b,
g(x)=x2+cx+d,又f(2x+1)=4g(x),且![]() ,f(5)=30,则g(4)=
.
,f(5)=30,则g(4)=
.
三、 解答题:
11、已知函数f(x)=x3+bx2+cx+d在(-∞,0)上是增函数,在[0,2]是减函数,且方程f(x)=0有三个根,它们分别是α,2,β.
⑴求c的值;⑵求证:f(1)≥2。
12、设![]() ,求函数
,求函数![]() 的单调区间.
的单调区间.
13、用总长44.8m的钢条制做一个底面是等腰三角形的直三棱柱容器的框架,如果所制做容器的底面的腰长比底边长的一半长1m,那么底面的底边、腰及容器的高为多少时容器的容积最大(参考数据2.662=7.0756,3.342=11.1556)
答案:
1、 C; 2、D; 3、B; 4、A; 5、B; 6、D
7、![]() ; 8、-1; 9、
; 8、-1; 9、![]() ; 10、
; 10、![]() ;
;
11、⑴![]() ,∵f(x)在(-∞,0)上是增函数,在[0,2]上是减函数,∴当x=0时,f(x)取得极大值,∴
,∵f(x)在(-∞,0)上是增函数,在[0,2]上是减函数,∴当x=0时,f(x)取得极大值,∴![]() ,∴c=0。
,∴c=0。
⑵∵f(2)=0,∴d=-4(b+2), ![]() 的两个根分别是x1=0,x2=
的两个根分别是x1=0,x2=![]() ,∵函数f(x)在[0,2]上是减函数,∴x2=
,∵函数f(x)在[0,2]上是减函数,∴x2=![]() ≥2,∴b≤-3,
≥2,∴b≤-3,
∴f(1)=b+d+1=b-4(b+2)+1=-7-3b≥2.
12、解:![]() .
.
当![]() 时 ,
时 , ![]() .
.
![]()
(i)当![]() 时,对所有
时,对所有![]() ,有
,有![]() .
.
即![]() ,此时
,此时![]() 在
在![]() 内单调递增.
内单调递增.
(ii)当![]() 时,对
时,对![]() ,有
,有![]() ,
,
即![]() ,此时
,此时![]() 在(0,1)内单调递增,又知函数
在(0,1)内单调递增,又知函数![]() 在x=1处连续,因此,函数
在x=1处连续,因此,函数![]() 在(0,+
在(0,+![]() )内单调递增
)内单调递增
(iii)当![]() 时,令
时,令![]() ,即
,即![]() .
.
解得![]() .
.
因此,函数![]() 在区间
在区间![]() 内单调递增,在区间
内单调递增,在区间![]() 内也单调递增.
内也单调递增.
令![]() ,
,
解得![]() .
.
因此,函数![]() 在区间
在区间![]() 内单调递减.
内单调递减.
13、设容器底面等腰三角形的底边长为2xm,则腰长为(x+1)m,高为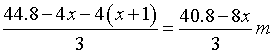 ,设容器的容积为Vm3,底面等腰三角形底边上的高
,设容器的容积为Vm3,底面等腰三角形底边上的高![]()
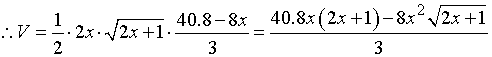
由x>0及![]() 得0<x<5.1,
得0<x<5.1,
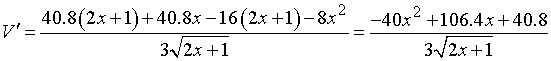 ,
,
令![]() ,得x2-2.66x-1.02=0,(x-3)(x+0.34)=0,由x>0,解得x=3,
,得x2-2.66x-1.02=0,(x-3)(x+0.34)=0,由x>0,解得x=3,
当0<x<3时,![]() ;当3<x<5.1时,
;当3<x<5.1时,![]() ,因此当x=3时,V有最大值。这时容器的底面等腰三角形的底边长为6m,腰长为4m,容器的高为5.6m.
,因此当x=3时,V有最大值。这时容器的底面等腰三角形的底边长为6m,腰长为4m,容器的高为5.6m.