导数的概念及运算复习指导

导数的概念及运算复习指导

　重点难点分析：
　　1．导数的定义、意义与性质：
　　（1）函数的导数：对于函数f(x)，当自变量x在x₀处有增量Δx，则函数y相应地有改变量Δy=f(x₀+Δx)-f(x₀)，这两个增量的比叫做函数y=f(x)在x₀到x₀+Δx之间的平均变化率，即。如果当Δx→0时，有极限，我们说函数在x₀处可导，并把这个极限叫做f(x)在x₀处的导数（或变化率）。记作f'(x₀)或，即。
　　（2）导函数：如果函数y=f(x)在开区间(a,b)内每一点处可导，这时，对于开区间(a,b)内的每一个值x₀，都对应着一个确定的导数f'(x₀)，这样就在开区间(a,b)内构成一个新的函数，我们把这一新函数叫做f(x)在区间内的导函数，记作f'(x)或y'，即。
　　（3）可导与连续的关系：如果函数y=f(x)在点x₀处可导，那么函数y=f(x)在点x₀处连续。
　　（4）导数的几何意义：过曲线y=f(x)上任意一点(x,y)的切线的斜率就是f(x)在x处的导数，即。也就是说，曲线y=f(x)在点P(x₀，f(x₀))处的切线的斜率是f'(x₀)，切线方程为y-y₀=f'(x₀)(x-x₀)。
　　2．求导数的方法：
　　（1）求函数y=f(x)在x₀处导数的步骤： 　　　 ① 求函数的增量Δy=f(x₀+Δx)-f(x₀)
　　 ② 求平均变化率　 ③ 取极限，得导数。
　　（2）几种常见函数的导数公式：
　　　　 ① C'=0(C为常数)；　　　　② (xⁿ)'=nx^n-1 (n∈Q )；
　　　　 ③ (sinx)'=cosx；　　　　　 ④ (cosx)'=-sinx；
　　　　 ⑤ (e^x)'=e^x；　　　 　　　　⑥ (a^x)'=a^xlna
　　　　 ⑦ ；　　　　　 ⑧
　　（3）导数的四则运算法则：
　　　　 ①(u±v)'=u'±v' 　　　　 ②(uv)'=u'v+uv' 　　　　 ③
　　（4）复合函数的导数
　　复合函数对自变量的导数，等于已知函数对中间变量的导数，乘以中间变量对自变量的导数。
　　说明：
　　1．函数的导数实质是一个极限问题，不应理解为平均变化率，而是平均变化率的极限。
　　2．求函数的导数要熟练掌握求导公式，特别是复合函数的导数要学会合理地分析
　　3．搞清导数的几何意义，为解决实际问题，如切线，加速度等问题打下理论基础。
　　典型例题：
　　例1．求下列函数的导数
　　①y=(2x-3)⁵　　②　　③　　④y=sin³2x
　　解析：① 设u=2x-3，则y=(2x-3)⁵分解为y=u⁵，u=2x-3 　由复合函数的求导法则得：
　　y'=f'(u)u'(x)=(u⁵)'(2x-3)'=5u⁴·2=10u⁴＝10(2x-3)⁴
　　② 设u=3-x，则可分解为，
　　。
　　③
　　 　　　　
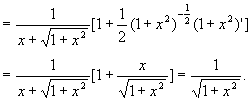
　　④ y'=3(sin2x)²·(sin2x)'=3sin²2xcos2x(2x)'=6·sin²2x·cos2x
　　例2．已知曲线，问曲线上哪一点处切线与直线y=-2x+3垂直，并写出这一点切线方程。
　　解析：，令，即，
　　得x=4，代入，得y=5，
　　∴曲线在点(4,5)处的切线与直线y=-2x+3垂直，切线方程为，即x-2y+6=0。
　　例3．已知曲线C：y=3x⁴-2x³-9x²+4。
　　① 求曲线C上横坐标为1的点的切线方程； ② 第①小题中切线与曲线C是否还有其它公共点。
　　解析：①把x=1代入C的方程，求得y=-4，∴ 切点为(1,-4)，y'=12x³-6x²-18x
　　∴ 切线斜率为k=12-6-18=-12，∴ 切线方程为y=-12x+8。
　　②由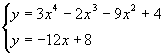 　得3x⁴-2x³-9x²+12x-4=0，即(x-1)²(x+2)(3x-2)=0，。
　　公共点为(1,-4)（切点），，除切点外，还有两个交点。
　　评析：举例说明曲线与直线相切并不说明只有一个公共点，当曲线是二次曲线时，我们知道直线与曲线相切，有且只有一个公共点，这种观点对一般曲线不一定正确。
　　*例4．设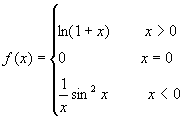，求f'(x)。
　　解析：当x>0时，，当x<0时，，
　　由于x=0是该函数的分界点，由导数定义知
　　
　　
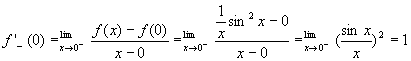
　　由于f'₊(0)=f'_-(0)=1，故有f'(0)=1于是：，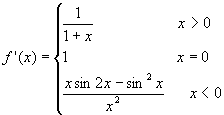
　　即：。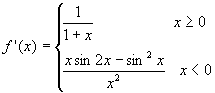

　　例5．已知使函数的导数为0的x值也使y值为0，求常数a。
　　解析：y'=3x²+2ax，令y'=0，得x=0或，
　　由题设x=0时，y'=y=0，此时，∴a=0；当时也解出a=0。
　　训练题：
　　1．已知函数，且f'(1)=2，则a的值为______。
　　2．设f(x)=xlnx，则f'(2)=________。
　　3．给出下列命题：
　　①；　②(tanx)'=sec²x
　　③函数y=x-1在x=1处可导；　④函数y=x-1在x=1处连续。
　　其中正确的命题有：_____。
　　4．函数y=cosx在点处的切线方程为_______。
　　5．已知函数f(x)=ax⁴+bx³+cx²+dx+e为偶函数，它的图象过点A(0,-1)，且在x=1处的切线方程为2x+y-2=0，求函数y=f(x)的表达式。
　　参考答案：
　　1. 2　　2. 　　3. ②，④　　4.
　　5．解：∵ f(x)是偶函数，f(-x)=f(x)，∴ b=d=0，f(x)=ax⁴+cx²+e，
　　又∵ 图象过点A(0，-1)，∴ e=-1，∴ f(x)=ax⁴+cx²-1，f'(x)=4ax³+2cx，
　　当x=1时，f'(1)=4a+2c=-2......① 　　对于2x+y-2=0，当x=1时，y=0。
　　∴ 点(1,0)在f(x)图象上，a+c-1=0........②
　　由①，②解出a=-2，c=3，　　因此f(x)=-2x⁴+3x²-1。