导数的应用复习指导

导数的应用复习指导

重点难点分析：
　　1．函数f(x)在区间(a,b)内是单调递增或递减的判定可依据单调性定义也可利用导数，应根据问题的具体条件适当选用方法，有时须将区间(a,b)划分成若干小区间，在每个小区间上分别判定单调性。
　　2．函数极值只反映函数在某点附近值的大小情况。在某区间上函数的极值可能有若干个，而且极小值未必小于极大值。f'(x₀)=0仅是函数f(x)在点x₀处有极值的必要条件，点x₀是f(x)的极值点，当且仅当在x₀的左右f'(x)的符号产生变化。
　　3．函数的最值表示函数在定义域内值的整体情况。连续函数f(x)在闭区间[a,b]上必有一个最大值和一个最小值，但是最值点可以不唯一。
　　4．在实际问题中，要由实际问题的背景构造出相应的函数关系式y=f(x),并注明其定义域，当f'(x)=0在定义域内只有一个解时，并且最值一定存在，则此点即为函数f(x)的最值点。
　　典型例题

1 单调性问题
　　例1．已知f(x)=x²+1, g(x)=x⁴+2x²+2且F(x)=g(x)-λf(x), 试问：是否存在实数λ，使F(x)在(-∞,-1)上是减函数，且在(-1,0)上是增函数。
　　解：假设存在实数λ满足题设。
　　F(x)=g(x)-λf(x)=(x⁴+2x²+2)-λ(x²+1)=x⁴-(λ-2)x²+(2-λ),
　　F'(x)=4x³-2(λ-2)x, 　　令4x³-2(λ-2)x=0, 　　若λ≤2，则x=0。
　　当x∈(-∞,0)时，F'(x)<0；当x∈(0,+∞)时，F'(x)>0。
　　∴ F(x)在(-∞,0)上单调递减，在(0,+∞)上单调递增，显然不符合题设。
　　若λ>2，则x=0或，

　当时，F'(x)<0； 　　当时，F'(x)>0；

　　当时，F'(x)<0；　　　当时，F'(x)>0。
　　∴ F(x)的单调增区间是，，

单调减区间是，。
　　要使F(x)在(-∞,-1)上是减函数，且在(-1,0)上是增函数，则，即λ=4。
　　故存在实数λ=4，使F(x)在(-∞,-1)上是减函数，且在(-1,0)上是增函数。
　　例2．设f(x)=ax³+x恰有三个单调区间，试确定a的取值范围，并求其单调区间。
　　解析：f'(x)=3ax²+1，若a≥0, f'(x)>0，对x∈R恒成立，此时f(x)只有一个单调区间，矛盾。
　　若a<0，∵ f'(x)=,此时f(x)恰有三个单调区间。
　　∴ a<0且单调增区间为，单调增区间为。
　例3．若函数f(x)=ax³+bx²+cx+d(a≠0) 满足条件f(0)=f(x₁)=f(x₂)=0(0<x₁<x₂), 且在[x₂, +∞]上

f(x)单调递增，求实数b的取值范围。
　　解：∵ f(0)=0, ∴ d=0。又∵ f(x₁)=f(x₂)=0,
　　∴ f(x)=ax(x-x₁)(x-x₂)=ax³-a(x₁+x₂)x²+ax₁x₂x,
　　∴ b=-a(x₁+x₂), f'(x)=3ax²-2a(x₁+x₂)x+ax₁x₂。
　　∵ f(x)在[x₂,+∞]上单调递增，∴ f'(x₂)≥0，即,
　　∴ ax₂(x₂-x₁)≥0, ∵ a≠0, x₂>x₁>0, x₂-x₁>0, ∴ a>0,
　　又∵ x₁+x₂>0, ∴ b=-a(x₁+x₂)<0, 故实数b的取值范围是(-∞,0)。

2 最（极）值问题
　　例4．已知函数f(x)=x³+ax²+bx+a²在x=1处有极值为10，求a,b的值。
　　解：f'(x)=3x²+2ax+b=0有一个根x=1, 　　故3+2a+b=0.....(1)
　　又f(1)=10, 故1+a+b+a²=10.....(2) 　　联立(1),(2)，消去b得，a²-a-12=0。
　　由此可得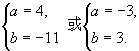
　　当a=-3，b=3时，f'(x)=3(x-1)²≥0，这时f(x)在x=1处无极值，不合题意。
　　当a=4, b=-11时，f'(x)=3x²+8x-11=(3x+11)(x-1)，时，f'(x)<0, x>1时，f'(x)>0。
　　这时x=1是极小值点， 故a=4, b=-11。
　　例5．求函数y=2e^x+e^-x的极值。
　　解析：y'=2e^x-e^-x，令y'=0, 即2e^2x=1,
　　列表：

x
y'	-	0	+
y	↘	极小值	↗

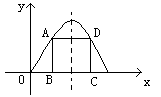∴ y_极小。
　　例6．求函数f(x)=3x-x³在闭区间的最大值和最小值。
　　解析：f'(x)=3-3x², 令f'(x)=0，则x₁=-1，x₂=1。
　　则f(-1)=-2, f(1)=2，又, 　

∴ [f(x)]_max=2, [f(x)]_min=-18。
　　例7．如右图所示，在二次函数f(x)=4x-x²的图象与x轴所围成图形中有个内接矩形ABCD，求 这个矩形面积的最大值。
　　解析：设点B的坐标为(x,0)且0<x<2,
　　∵ f(x)=4x-x²图象的对称轴为x=2, ∴点C的坐标为(4-x,0),
　　∴ BC=4-2x, BA=f(x)=4x-x²。
　　∴ 矩形面积为y=(4-2x)(4x-x²)=16x-12x²+2x³ 　　　 y'=16-24x+6x²=2(3x²-12x+8)
　　令y'=0，解得，∵ 0<x<2, ∴ 取。
　　∵ 极值点只有一个，当时，矩形面积的最大值。

　3 切线问题
　　例8．若直线y=3x+1是曲线y=ax³的切线，试求a的值。
　　解：设直线y=3x+1与曲线y=ax³相切于点P(x₀, y₀)，由y=ax³得，y'=3ax²，所以
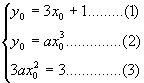　　，由(1),(2)得。 由(3)得，将它代入上式可得3x₀+1=x₀,
　　∴ , ∴ , ∴ a=4。
　　例9．已知二次函数f(x)的图象过点(-1,0)，且不等式对一切实数x都成立，求函数f(x)解析式。
　　解：设函数f(x)=ax²+bx+c (a≠0)。 　　∵ 函数f(x)的图象过点(-1, 0),
　　∴ a-b+c=0........(1), ∵ , 　　∴ ,　
　　∴ f(1)=1。 　　∴ a+b+c=1......(2)
　　由(1),(2)可得，，从而。
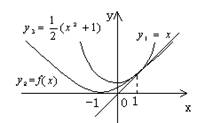
　　令y₁=x, y₂=f(x), , 作图，f(x)的图象夹在y₁=x, 之间，
　　又y₁=x与只有唯一公共点（1，1），
　　故直线y₁=x与y₂=f(x)，相切于同一点（1，1）。
　　∵ , 而f '(1)=1, 即，
　　∴ ，故。

4. 应用问题
　　例10．用总长14.8m的钢条制作一个长方体容器的框架，如果所制作容器的底面的一边比另一边长0.5m，那么高为多少时容器的容积最大？并求出它的最大容积。
　　解：设容器底面短边为xm，则另一边长为(x+0.5)m, 高为。
　　由3.2-2x>0且x>0，得0<x<1.6。
　　设容器的容积为ym³，则有y=x(x+0.5)(3.2-2x)=-2x³+2.2x²+1.6x, (0<x<1.6)
　　∴ y'=-6x²+4.4x+1.6=0, 即15x²-11x-4=0，解得（不合题意，舍去）。
　　当x∈(0,1)时，y'>0；当x∈(1,1.6)时，y'<0。
　　∴ 函数y=-2x³+2.2x²+1.6x在(0,1)上单调递增，在[1，1.6]上单调递减。
　　因此，当x=1时，y_max=-2+2.2+1.6=1.8，这时，高为3.2-2×1=1.2。
　　故容器的高为1.2m时容器最大，最大容积为1.8m³。
　　例11．一艘渔艇停泊在距岸9km处，今需派人送信给距渔艇km处的海岸渔站，如果送信人步行每小时5km，船速每小时4km，问应在何处登岸再步行可以使抵达渔站的时间最省？
　　解析：如图示设A点为渔艇处，BC为海岸线，C为渔站，且AB=9km,
　　设D为海岸线上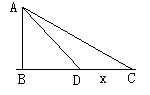一点，CD=x，只需将时间T表示为x的函数，
　　∵ ，
　　由A到C的时间T，则（0≤x≤15）
　　（0≤x≤15）
　　令T'=0，解得x=3，在x=3附近，T'由负到正，
　　因此在x=3处取得最小值，又，比较可知T(3)最小。
　　训练题：
　　1．函数y=4x²(x-2), x∈[-2，2]的最小值是_____。
　　2．一个外直径为10cm的球，球壳厚度为，则球壳体积的近似值为____。
　　3．函数f(x)=x⁴-5x²+4的极大值是______，极小值是_____。
　　4．做一个容积为256升的方底无盖水箱，问高为多少时最省材料？
　　参考答案：
　　1. –64　　2. 19.63cm³　　3. 4；
　　4. 设高为h，底边长为a，则所用材料为S=a²+4ah,而a²h=256，a∈(0,+∞),
　　∴ , a∈(0,+∞), 　　令S'(a)=, ∴ a=8。
　　显然当0<a<8时，S'(a)<0，当a>8时，S'(a)>0，因此当a=8时，S最小，此时h=4。