高考数学复习高一期末总复习题
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.
1． 已知
（ ）
A．
B．－ C．
D．－
2．等差数列
（ ）
A．48 B．49 C．50 D．51
3．设函数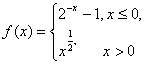
若
，则x0的取值范围是（ ）
A．（－1，1） B．（－1，+∞）
C．（－∞，－2）∪（0，+∞） D．（－∞，－1）∪（1，+∞）
4．函数
的反函数为 （ ）
A．
B．
C．
D．
5．函数
的最大值为 （ ）
A．
B．
C．
D．2
6．已知方程
的四个根组成的一个首项为
的等差数列，则 
（ ）
A．1 B．
C．
D．
7．函数
（ ）
A．
B．
C．
D．
8．设集合
等于（ ）
A．
B．
C．
D．
9．设
，则 （ ）
A．y3>y1>y2 B．y2>y1>y3 C．y1>y2>y3 D．y1>y3>y2
10．“
”是“
”的 （ ）
A．必要非充分条件 B．充分非必要条件
C．充分必要条件 D．既非充分又非必要条件
11．已知函数
是定义在[a，b]上的减函数，那么
是（ ）
A．在
上的增函数 B．在
上的增函数
C．在上的减函数 D．在上的减函数
12．条件“
”是条件“
”的 （ ）
A．充分但非必要条件 B．必要但非充分条件
C．充要条件 D．既非充分又非必要条件
13．已知x，y为正实数，且
成等差数列，
成等比数列，那么
的取值范围是 （ ）
A．
B．
C．
D．
14．设
是锐角三角形的两个互不相等的内角，若
，
则
这间的大小关系是 （ ）
A．
B．
C．
D．
15．集合
，映射
，使任意
，都有
是奇数，则这样的映射共有 （ ）
A．60个 B．45个 C．27个 D．11个
二、填空题：把答案填在题中横线上.
16．使
成立的
的取值范围是
.
17．函数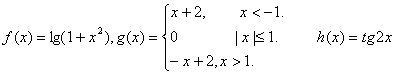
中，
是偶函数.
三、解答题： 解答应写出文字的说明，证明过程或演算步骤.
18．本小题考查数列，等比数列，等比数列求和等基础知识，考查运算能力，满分12分.
已知数列
（Ⅰ）求
（Ⅱ）证明
解：（Ⅰ）∵a1=1 . ∴a2=3+1=4, a3=32+4=13 .
（Ⅱ）证明：由已知an－an－1=3n－1,故
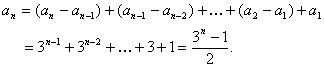所以证得
.
19．本小题主要考查三角函数的图象和单调性，奇偶性等基本知识，以及分析问题和推理计算能力，满分12分.
已知函数
是R上的偶函数，其图象关于点
对称，且在区间
上是单调函数.求
的值.
解：由f(x)是偶函数，得f(－x)= f(－x).
即： 
所以－
对任意x都成立，且
所以得
=0. 依题设0
，所以解得
，由f(x)的图象关于点M对称，得
.
取x=0,得
=－，所以=0.
20．（本小题满分12分）已知
设P：函数
在R上单调递减.
Q：不等式
的解集为R，如果P和Q有且仅有一个正确，求
的取值范围.
解：函数在R上单调递减
不等式
21．（本小题满分12分，附加题4分）（Ⅰ）设
是集合
中所有的数从小到大排列成的数列，即
将数列
各项按照上小下大，左小右大的原则写成如下的三角形数表：
3
5 6
9 10 12
— — — —
— — — — —
（i）写出这个三角形数表的第四行、第五行各数； （i i）求
.
（Ⅱ）（本小题为附加题，如果解答正确，加4分，但全卷总分不超过150分）
设
中所有的数都是从小到大排列成的数列，已知
（Ⅰ）解：（i）第四行17 18 20 24 第五行 33 34 36 40 48
（i i）设
，只须确定正整数
数列中小于
的项构成的子集为 
其元素个数为
满足等式的最大整数
为14，
所以取
因为100－
（Ⅱ）解：
令
因
现在求M的元素个数：
其元素个数为
：
某元素个数为
某元素个数为
22．本小题主要考查三角函数的倍角、和角公式，以及三角函数的性质等基本知识，考查运算能力，满分13分.
已知函数
（Ⅰ）求
的最小正周期；（Ⅱ）若
，求的最大值、最小值.
（Ⅰ）解：因为
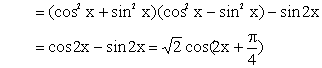
所以的最小正周期
（Ⅱ）解：因为
所以
当
时，
取得最大值
；当
时，
取得最小值－1. 所以
在
上的最大值为1，
最小值为－
23．本小题主要考查等差、等比数列等基本知识，考查综合运用数学知识和方法解决问题的能力.满分13分.
已知数列
是等差数列，且
（Ⅰ）求数列的通项公式；
（Ⅱ）令
求数列
前n项和的公式.
（Ⅰ）解：设数列公差为
，则 
又
所以
（Ⅱ）解：令
则由
得
①
②
当
时，①式减去②式，得
所以
当
时, 
综上可得当时,
当时，
24．本小题考查函数、不等式等基本知识，考查综合运用数学知识分析问题和解决问题的能力.满分14分.
设是定义在区间
上的函数，且满足条件：
（i）
（ii）对任意的
（Ⅰ）证明：对任意的
（Ⅱ）证明：对任意的
（Ⅲ）在区间[－1，1]上是否存在满足题设条件的奇函数，且使得
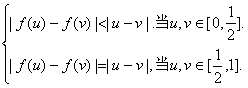
若存在，请举一例：若不存在，请说明理由.
解：（Ⅰ）证明：由题设条件可知，当
时，有
即
（Ⅱ）证法一：对任意的
当
不妨设
则
所以，
综上可知，对任意的
都有
证法二：由（Ⅰ）可得，
当
所以，当
因此，对任意的
当
时，
当
时，有
且
所以
综上可知，对任意的
都有
（Ⅲ）答：满足所述条件的函数不存在.
理由如下，假设存在函数满足条件，则由
得
又
所以
①
又因为为奇数，所以
由条件
得
② ①与②矛盾，所以假设不成立，即这样的函数不存在.
25．（本小题满分14分）
已知函数
的最大值为
，其最小正周期为
.
（1）求实数
的值.
（2）写出曲线的对称轴方程及其对称中心的坐标.
解：（1）
………………………4分
…………………………6分
∵y的最小正周期T=π， 
……………………8分
…………………………10分
（2）由（1）知
， 
.
∴曲线的对称轴方程为
.…………………………12分
对称中心的坐标为
……………………………………………14分
26．（本小题满分14分）
设定义在上的函数满足；
（1）对于任意正实数a、b，都有
，其中p是正实常数；
（2）
；
（3）当
时，总有
.
（Ⅰ）求
的值（写成关于p的表达式）；
（Ⅱ）求证
上是减函数；
（Ⅲ）（理科学生作）设
，数列的前n项和为Sn，当且仅当n=5时，Sn取得最大值. 求p的取值范围.
（文科学生作）设，求数列的前n项和Sn .
解（1）取a=b=1，则
…………2分
又
. 且.
得：
………………4分
（2）设
研究：
………………6分 依
再依据当时，总有成立，可得
………………8分
即
成立，故上是减函数.………………9分
（3）
……………………………………11分
又
. 
数列是以
为首项，
公差为－1的等差数列.……………………………………12分
.
由题意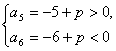
………………………………………14分
（文科）
……………………14分