高考单元与专题复习质量评估优化训练（5）
数列（综合）
一、选择题（本大题共12小题，每小题5分，共60分）
1．在等差数列{
}中，若
－
－
－
＋
＝－6，则的值为（ ）
A．102 B．98 C．108 D．以上都不对
2．一个首项为正数的等差数列{}，前3项之和与前11项之和相等，则前（ ）项和最大（ ）
A．6 B．7 C．8 D．以上都不对
3．对于每个自然数n，抛物线
与x轴交于
、
两点，以表示两点问的距离，则
+
+…＋
的值是（ ）
A．
B．
C．
D．以上都不对
4．△ABC中，tanA是以－4为第三项，－1为第七项的等差数列的公差，tanB是以
为第三项，4为第六项的等比数列的公比，则该三角形的形状是（ ）
A．钝角三角形 B．锐角三角形 C．等腰直角三角形 D．以上均错
5．数列{}的前n项和为
，下列几个命题：
①若{}是等比数列，且
，则
；
②若{}是等差数列，则
也成等差数列；
③若{}是等比数列。则也成等比数列；
④若{}是等比数列，则数列
可能是等差数列．其中正确的命题是（ ）
A．①②③④ B．①②③ C．②④ D．以上都不对
6．数列{}是公差不为零的等差数列，并且
是等比数列
的相邻三项．若
＝5，则
等于（ ）
A．
B．
C．
D．
7．已知数列{}中，
，
，
，且
，则
的值为（ ）
A．4009 B．4010 C．4011 D．以上都不对
8．各项均为实数的等比数列{}的前n项和为，若
＝10，
＝70，则
的值为（ ）
A．150或－200 B．－200 C．150 D．以上都不对
9．在等差数列{}中，公差d
O，且
，则数列的前（ ）项和最小。
A．20 B．10或30 C．40 D．以上都不对
10．{}满足
，
，则等于（ ）
A．
B．
C．
D．以上都不对
11．在数列{}中，
，且
，
，n∈N，则
的值为（ ）
A．2 B．4 C．5 D．6
12．在圆
内，过点(
，
)有n条弦的长度成等差数列，最短弦长为数列的首项，最长弦长为，若公差d∈[
，
]，那么n的取值集合为（ ）
A．{4，5，6) B．{6，7，8，9} C．{3，4，5) D．{3，4，5，6}
二、填空题(本大题共4小题，每小题4分，计16分)
13．已知等差数列{}中，
，则的最大值为
．
14．设
，那么和式
的值等于
．
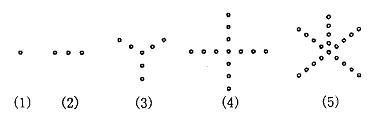
15．(由2004年上海春季高考题改编)根据下列5个图形及相应点的个数的变化规律，试猜测第n+1个图中有 个点．
16．一个球从100米高处自由落下，每次着地后又跳回到原高度的一半落下，当它第10次着地时，共经过了 米(要求取整数)．
三、解答题(本大题共6小题，计74分)
17．(本题满分12分)已知函数
．
(1)求反函数
，并指出其定义域；
(2)若正数数列{}的前n项和为，且
，
(n≥2)，求数列{}的通项．
18．(本题满分12分)在公差不为零的等差数列{}和等比数列{}中，已知
，问是否存在常数a、b，使得对于一切自然数n都有
成立?若存在，求出a、b；若不存在，说明理由．
19．(本题满分12分)设f(x)=(x－1)
，g(x)＝4(x－1)，数列{}满足=2，f(
)＝(－
)g()，数列{
}满足＝)－g()
(1)求；
(2)求数列{
}中的最大值和最小值．
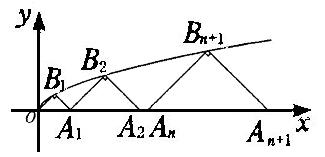
20．(本题满分12分)如图，
在x轴正半轴上，
在曲线
上．若△
，△
，△
，…均为等腰直角三角形，且
为直角顶点，求前100个等腰直角三角形的面积之和．
21．(本题满分12分)买一套新住房需15万元，若一次将款付清可优惠25％；若连续五年分期将款付清，则需在每年相同的月份内交付3万元．如果银行一年期存款的利率为8％，按本利累进计算(即每年的付款与利息之和转为下年的存款)．问：两种付款办法哪种对购房者有利?试说明理由．
22．(本题满分14分)设
，
是函数
(x∈R)图象上的两点，且线段
中点P的横坐标是．
(1)求证：点P的纵坐标是定值；
(2)若数列{}的通项公式
，(m∈N，n＝1，2，…，m)，求数列{}的前m项和
；
(3)若m∈N时，不等式
恒成立，求实数a的取值范围．
参考答案：
