数列与极限(一)

数列与极限(一)

1、若构成　　　　　 （　　）

A．等差数列 B．等比数列C．是等差数列也是等比数列D．不是等差数列也不是等比数列

2、若四个正数a，b，c，d成等差数列，x是a和d的等差中项，y是b和c的等比中项，则x和y的大小关系是　　　　　　　　　　　　　　　　　　　　　　　　  （　　）

　　　 A．x<y　　　　　　　　　　 B．x>y　　　　　　　　　　 C．x=y　　　　　　　　　　 D．x≥y

3、若一个等差数列前3项的和为34，最后3项的和为146，且所有项的和为390，则这个数列有　　　 （　　）A．13项　　　　　　　 B．12项　　　 　 C．11项　　　　 D．10项

4、一张报纸，其厚度为a，面积为b，现将此报纸对折（既沿对边中点的连线折叠）7次，

这时报纸的厚度和面积分别是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．　　　　　　　　B．　　　　　 C．　　　　 D．

5、凸n边形的各内角度数成等差数列，最小角是，公差为，则边数n等于（　　）

A．9　　　　　　　　　　　　B．12　　　　　　　　　　　 C．16　　　　　　　　　　　D．18

6、在等差数列{}中，若其前n项和，则

的值　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．大于4　　　　　　　　B．等于4　　　　　　　　 C．小于4　　　　　　　　D．大于2且小于4

7、等差数列的前n项和分别为与，若，则的值是（　　）

A．　　　　　　　　　　　B．　　　　　　　 C．　　　　　　　D．

8、已知等比数列的公比是2，且前4项的和是1，那么前8项之和为　　　　　　　　　　　（　　）

　　　 A．15　　　　　　　　　　　B．17　　　　　　　　　　　 C．19　　　　　　　　　　　D．21

9、已知等差数列的前n项和为S_n，若等于　　　　　　　　　　　　（　　）

　　　 A．18　　　　　　　　　　　B．36　　　　　　　　　　　 C．54　　　　　　　　　　　D．72

10、一个等差数列共有n项(n>10), 其前10项之和为50，后10项之和为70，则这n项的和为（　）。（A）120　（B）60(n－10) (n>10)　（C）12n (n>10)　（D）6n (n>10)

11、设等比数列{q}(q>1, n∈N)的前n项和为S _n，则等于（　）。

　 （A）q²　（B）1　（C）　（D）0

12、某人于1997年7月1日去银行存款元，存的是一年定期储蓄，1998年7月1日他将到期的本息一并取出，再加元后，又存一年定期储蓄。此后每年的7月1日分都按照同样的方法，在银行存款和取款，设银行一年定期储蓄的年利率不变，则到2002年7月1日，他将所有的存款和利息全部取出时，取出的钱数共为

（A）元　（B）元　（C）元　（D）

13、已知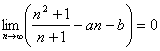，则点M所在的象限是　　　　　　　　（　　）

　　　A．第一象限　　　　　　 B．第二象限　　　　　 C．第三象限　　　　　　 D．第四象限　　  

14、若存在，则实数的取值范围是　　　　　　　　　　　　　　

　　　A．　　　　　　　　　B．　　　　　　　　C． 　　　　　　　　D．

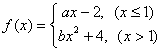15、设，而　则直线的倾斜角是（　）

　　　A．　　　　　　　B． 　　　 C．　　　　 D．

16、以边长为1的正六边形的一边为边向外作正方形，以正方形的一边为底向外作等腰直角三角形，再以等腰直角三角形一条直角边为边向外作正六边形，……，如此继续无限反复同一过程，则这些正六边形、正方形、等腰直角三角形面积之和为　　　　 （　　）

A． 　 B．　C． D．

17、已知，则的值是　

A．1　　　　　 B．2　　 C．　　　　  　　D．

18、已知的值是　　

　　　　　　　　　　　 （　　）

A．　　 B．　 C．　　  D．

19、考察以下4个命题：①若成等差数列，则②若成等比数列，则③若则成等差数列；④若则成等比数列，这4个命题中，假命题是(　)　A　 ①　 B　 ②　　C　　③　 D　　④

20、一个递减等差数列的首项是4，且第1项，第4项，第2项恰好是某个等比数列的连续三项，则S₁₀=______

21、已知数列{a_n}的通项公式a_n=9-2n，则H_n= a₁+ a₂+…+ a_n=　　　　　 　．

22、设是满足的整数，若，，成等比数列，则 的值依次为　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．2, 4, 8　　　 　　 B．3, 6, 9　　　　　　 C．2, 6, 8　　　　  D．2, 4, 9

23、已知

　　　　　 ．

24、一系列椭圆以定值线l为准线，所有椭圆的中心都在定点M，点M到l的距离为2，若这一系列椭圆的离心率组成以为首项，公比为的等比数列，而椭圆相应的长轴长为C_n，则为　　　　　　　  .

25、已知等比数列{}的前n项和为为常数），则公比q等于

　　　　 ，等于　　　　　  .

数列与极限(二)

1、一等差数列前n项和为30，前2n项和为100，则它的前3n项和为（　）。

（A）130　　（B）170　　（C）200　　（D）210

2、若lg²＝4lglg，则a, b, c（　）。

　（A）成等差数列　　　　　　　  （B）成等比数列

　（C）既成等差数列，又成等比数列（D）既不成等差数列，又不成等比数列

3、在等差数列{a_n}中，若S₄＝1, S₈＝4，则a₁₇＋a₁₈＋a₁₉＋a₂₀的值为（　）。

（A）7　　（B）8　　（C）9　　（D）10

4、若abc≠0, a, b, c互不相等，且a, b, c顺次成等差数列，又a, c, b顺次成等比数列，则a:b:c（　）。　（A）(－4):1:3　（B）(－1):2:3　（C）3:1:(－2)　（D）4:1:(－2)

5、在等比数列{a_n}中，a₁＝1, 已知对于任意的自然数n有a₁＋a₂＋a₃＋……＋a_n＝2ⁿ－1，则a₁²＋a₂²＋a₃²＋……＋a_n²等于（　）。

（A）(2ⁿ－1)²　（B）(2ⁿ－1)　（C）4ⁿ－1　（D）(4ⁿ－1)

6、等比数列{a_n}中，若各项均为正，且公比q≠1，则（　）。

（A）a₁＋a₈>a₄＋a₅　 （B）a₁＋a₈<a₄＋a₅

（C）a₁＋a₈＝a₄＋a₅　（D）a₁＋a₈与a₄＋a₅的大小关系不确定

7．无穷等比数列{a_n}的公比为q，q<1，首项a₁＝1，若其每一项都等于它后面所有项的和的k倍，则k的取值范围是（　）。

（A）[0, ＋∞)　　　　　　　  （B）(－∞, －2)　

（C）(－∞, －2)∪(0, ＋∞)　　（D）(－2, 0)

8、等差数列{a_n}中，前n项和为S_n，a₃＝a₉，公差d<0，若存在自然数N，对于任意的自然数n，总有S_n≤S_N，则N等于（　）。

（A）7和8　（B）6和7　（C）5和6　（D）4和5

9、已知a_n＝ (n∈N)，则在数列{a_n}的前30项中最大项和最小项分别是（　）。

（A）a₁₀, a₃₀　（B）a₁₀, a₉　（C）a₁, a₃₀　（D）a₁, a₉

10、无穷等比数列{a_n}的各项和等于3，第二项为－，则此数列奇数项的和为（　）。

　 （A）3　（B）－　（C）　（D）16

11、等于（　）。

　 （A）1　　（B） 　 （C）0 　 （D）

12、已知各项均为正数的等比数列{a_n}的首项a₁=1,公比为q,前n项和为S_n,=1,则公比q的取值范围是：　 A.q≥1　　 B.0<q≤1　　C.0<q<1　　 D.q>1.

13、已知数列｛a_n｝的前ｎ项和为Sn，且Sn＝1＋，则　　　　　  

14、已知 , 则a = ____.

15、如果，则a的取值范围是____。

16、如果存在，则x的取值范围是_____

17、无穷等比数列的第一项等于第二项开始隔一项的以后各项的和的3倍,则这个数列的公比为　　　　　　　

18、已知{a_n}是公差不为零的等差数列，如果Sn是{a_n}的前n项的和，那么等于

19、一个等差数列的前四项和为21，末四项和为67，前n项和为286，则项数n为　　。

20、已知等比数列{a_n}的公比大于1，且a₇a₁₁=6,a₄+a₁₄=5,则=_______.

数列与极限(三)

1、一个等差数列共有10项，其中奇数项的和为，偶数项的和为15，则这个数列的第六项是 (　)　A  3　 B　 4　 C　 5　 D　 6

2、已知等差数列满足，则有 (　)

A  　 B　　C　　 D　

3、在等比数列中，则(　)

A  6　 B　 －6　 C　 　 D　

4、在1和2之间插入个数，组成首项为1，末项为2的等差数列，若此数列的前项的和与后项的和之比为9:13，则(　)

A  8　 B　 10　 C　12　 D　 14

5、设是递增等差数列，前三项和为12，前三项积为48，则它的首项是____

A  1　 B　2　 C　 4　　D　 6

6、若无穷等比数列的前n项的和为S_n，各项和为S，且S=S_n+2a_n,则的公比为(　)

A  　B　　 C　　 D　　

7、在等比数列中，已知，则数列前15项的和为(　)  A　　B　　C　5　 D　 15

8、在数列中，则的值为(　)

A  750　B　610　 C　510　 D　505

9、若关于的方程和的四个根可组成首项为的等差数列，则的值为(　)

A  　B　 　 C　 　 D　

10、数列中，若是首项为1，公比为的等比数列，则(　)　A  　B　　 C　 　 D　

11、某工厂1999年生产某种产品2万件，计划从2000年开始，每年的产量比上一年增长20%，经过年这家工厂生产这种产品的年产量超过12万件，则的值为

(已知lg2=0.3010,lg3=0.4771)(　 )　　A　10　 B　 11　 C　 12　 D　 13

12、某企业去年销售收入1000万元，年成本分为年生产成本500万元与年广告费成本200万元两部分，若利润的P%为国税，且年广告费超出年销售收入2%的部分也必须按P%征国税，其它不纳税，已知该企业去年共纳税120万元，则税率P%为(　)

A  10%　 B　12%　 C　　25%　 D　 40%

16、某种细胞开始有两个，1小时后分裂成4个并且死去1个，2小时后分裂成6个并且死去1个，3小时后分裂成10个并且死去1个，…，按照这种规律进行，6小时后细胞的存活数是　　　　　　　　　　　　　。

17、有一组数据：，它们的算术平均值为10，若去掉其中最大的，余下数据的算术平均值为9；若去掉其中最小的，余下数据的算术平均值为11. 则关于n的表达式为__　 ___；关于n的表达式为_　　 __.

18、给出下列四个命题：①等差数列各项的相反数依次构成等差数列；②等差数列中，任意两项之和仍是此数列的某一项；③公比大于1的等比数列是递增数列；④若不为1的正数成等比数列，则当时，成等差数列，其中不正确的命题的序号_________

19、某村镇1993年的人口为1万人，人均住房面积为5㎡，若该村镇每年人口的平均增长率为1%，欲使2003年人均住房面积达10㎡，则每年平均需新建住房______㎡

20．中，是以－4为第三项，－1为第七项的等差数列的公差，是以为第三项，4为第六项的等比数列的公比，则该三角形的形状是_________

21、在等差数列与等比数列中，则与的大小关系是_______

22、在等差数列中，若，则有等式

成立，类比这一性质，相应地在等比数列中，若则有等式_______

23、S_n表示一个公比的等比数列的前项的和，记，那么集合M的子集个数是_____

24、)的值为_____

25、已知公差不为零的等差数列的第项依次构成等比数列的连续三项，则等比数列的公比是________

26、已知实数成等差数列，成等比数列，则的取值范围是

27、若无穷等比数列的前项的和为S则该数列所有项的和为________

高考数列与极限专题复习

1、等差数列的前n项和为S_n,且如果存在正整数M，使得对一切正整数n，都成立.则M的最小值是　　　　　  .

2、已知数列1，成等差数列，成等比数列，则的值为　　  .

3、在等比数列中，

则用m、n表示为　　　　　　　　　　　　　　　　　　 .

4、已知，则=　　　　　 .

5、一个热气球在第一分钟时间里上升了25米高度，在以后的每一分钟里，它上升的高度都是它在前一分钟里上升高度的80%，这个热气球最多能上升　　　　　　　 米.

6、一动点由原点出发，首先向右移动1个单位到点，然后沿着原方向逆时针旋转 的方向，移动个单位到点，若照此继续下去，移动上次所移动距离的一半，求动点移动的极限位置__________

7、已知函数数列{a_n}是公差为d的等差数列，{b_n}是公比为q（q∈R且

q≠1）的等比数列，设（I）求数列{a_n}和{b_n}的通项公式；（II）设数列{c_n}的前n项和为S_n，如果对一切都有

成立，求

8、已知函数，设正项数列{}的首项，前n项和S_n满足（1）求的表达式；（2）在平面直角坐标系内，直线L_n的斜率为a_n,且L_n与曲线有且仅有一个公共点，L_n又与y轴交于点D_n（0，b_n）,当若求证：C₁+C₂+C₃…+C_n－n<1.

9、设各项均为正数的数列的前n项和为，对于任意的正整数n都有等式成立.（Ⅰ）求；（Ⅱ）求证;（III）求.

10、已知等比数列，若项数为且前项之和等于偶数项之和的11倍，第三项和第四项之和为第二项和第四项之积的11倍.(I) 求首项和公比；

(II) 若数列满足级前项和为，求及.

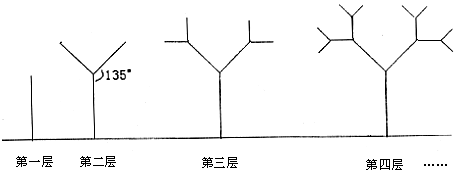
11、下图是树形图形。第一层是一条与水平线垂直的线段，长度为1；第二层在第一层线段的前端作两条与该线段成角的线段，长度为其一半；第三层按第二层的方法在每一线段的前端生成两条线段；重复前面的作法作图至第n层。设树的第n层的最高点到水平线的距离为n层的树形图的高度．（I）求第三层及第四层的树形图的高度；（II）求第n层的树形图的高度；（n为偶数）（III）求的值．

12、为促进个人住房商品化的进程，我国1999年元月公布了个人住房公积金贷款利率和商业性贷款利率如下：

贷款期(年数)	公积金贷款月利率(‰)	商业性贷款月利率(‰)
…… 11 12 13 14 15 ……	…… 4.365 4.455 4.545 4.635 4.725 ……	…… 5.025 5.025 5.025 5.025 5.025 ……

汪先生家要购买一套商品房，计划贷款25万元，其中公积金贷款10万元，分十二年还清；商业贷款15万元，分十五年还清．每种贷款分别按月等额还款，问：（I） 汪先生家每月应还款多少元?（II） 在第十二年底汪先生家还清了公积金贷款，如果他想把余下的商业贷款也一次性还清；那么他家在这个月的还款总数是多少?（参考数据：1.004455¹⁴⁴＝1.8966，1.005025¹⁴⁴＝2.0581，1.005025¹⁸⁰＝2.4651）

13、已知，若数列{a_n}

成等差数列.（1）求{a_n}的通项a_n;

（2）设 若{b_n­}的前n项和是S_n，且

14、已知二次函数的图象的顶点坐标是（Ⅰ）求的表达式，并求出f（1）、f（2）的值；（Ⅱ）数列{a_n}，{b_n}，若对任意的实数x都满足，其中是定义在实数R上的一个函数，求数列{a_n}，{b_n}的通项公式；（Ⅲ）设圆，若圆C_n与圆C_n+1外切，{r_n}是各项都是正数的等比数列，记S_n是前n个圆的面积之和，求.

15、若、，(Ⅰ)求证：；

(Ⅱ)令，写出、、、的值，观察并归纳出这个数列的通项公式；

(Ⅲ)求的值.

高考数列与极限专题复习参考解答

7、（I）由题意.

　

同理   

（II）

又{c_n}是首项为8，公比为－2的等比数列．

　

8、解：（1），

　　　 所以数列是以为首项、为公差的等差数列，……………………2分

　　　 ……………………4分

　　　 又…………………………………………5分

　　　 （2）设L_n：，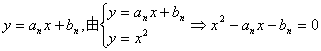

　　　 据题意方程有相等实根，…………7分

　　　 （另解：设L_n与的公共点为P（），则点P处的切线斜线率

　　　

　　　 令.）

　　　 当……9分

　　　 ……11分

…13分…………………………14分

9、Ⅰ．当n=1时，.Ⅱ．当时，

当n=1时，也符合

Ⅲ． 当时， 　 ，　　 于是数列是首项为2，公差为2的等差数列.

,　,

　　.

10、（I）由条件知：，依题意得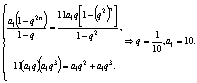　　  

　（II）　　

　　　   

　　　　

11、（I）逐一计算，得

_..　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

（II）当n为偶数时　　　　　　　　　　　　　　　　　　　　　

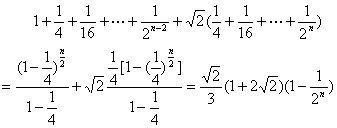
（III）由（II）知　　 　

12、设月利率为r，每月还款数为a元，总贷款数为A元，还款期限为n月.

第1月末欠款数　A(1＋r)－a,

第2月末欠款数　[A(1＋r)－a](1＋r)－a＝ A(1＋r)²－a (1＋r)－a,

第3月末欠款数　[A(1＋r)²－a (1＋r)－a](1＋r)－a＝A(1＋r)³－a (1＋r)²－a(1＋r)－a,

……

第n月末欠款数　,

得：.　　　　　　　　　　　 (I) 对于12年期的10万元贷款，n＝144，

r＝4.455‰,　∴,

对于15年期的15万元贷款，n＝180，r＝5.025‰,

∴.　 由此可知，汪先生家前12年每月还款942.37＋1268.22＝2210.59元，后3年每月还款1268.22元．　　　　　　　　　

(II) 至12年末，汪先生家按计划还款以后还欠商业贷款

.其中A＝150000，a＝1268.22，

r＝5.025‰ , ∴X＝41669.53.

再加上当月的计划还款数2210.59元，当月共还款43880.12元．　　

13、（14分）解：设2，f(a₁), f(a₂), f(a₃),……，f(a_n),2n+4的公差为d，则

2n+4=2+(n+2－1)dd=2,…………………………（2分）

……………………（4分）

　 （2），

　

　　　　

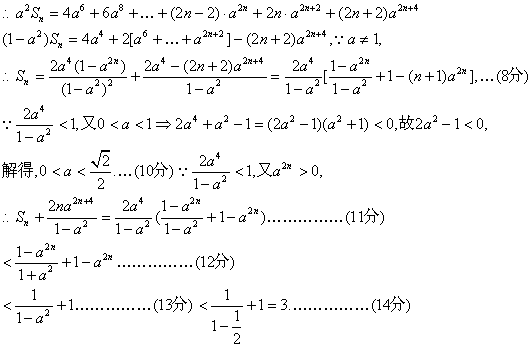
14、（I）由已知得　

　　　　

　　　　（II）　　　　　  ①

　　　　　　　　 ②

　　　　　　　　 由①②得

　　　　（III），设数列{r_n}的公比为q，则

　　　　　.

　　　　,

　　　　

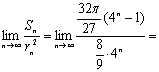
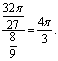
15、(I)若，即解得：

从而与题设矛盾，故原命题成立.

　 (Ⅱ) 、、、、,　.

（Ⅲ）.