高考单元与专题复习质量评估优化训练（六）
三角函数（基础）
【说明】本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分．请将第I卷选择题的答案填人答题栏内，第Ⅱ卷可在各题后直接作答．
第I卷(选择题共60分)
一、选择题（本大题共12小题，每小题5分，共60分）
1．函数
的周期是函数
的周期的2倍，则
等于( )
A．
B．1 C．2 D．4
2．函数
的递减区间是( )
A.
B．
C．
D．以上都不对
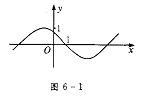3．右图是给定周期为2
的三角函数
的图象，那么
的解析表达式可写成( )
A．sin(1+x) B．sin(-1-x) C．sin(x-1) D．sin(1-x)
4．若
，则
的取值范围是( )
A．[-
，] B．[-
，] C．[-
，] D．[-
,]
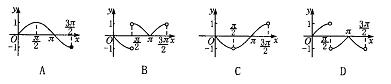
5．函数
的图象是( )
6．已知
，则
的值为( )
A．0 B．1 C.
D．以上都不对
7．
为三角形的一个内角，且函数
恒正，则（ ）
A．
B．
C．
D．
8．已知点P(
，tan
)在第一象限，则在[0，2)内的取值范围是（ ）
A．(
，
)
(
，
) B．(
，)(，)
C．(，)(，) D．(，)（，）
9．以下说法正确的是（ ）
A．若为第一象限角，则2是第二象限角
B．在第二象限内，函数y＝sinx和y＝cosx都是单调递减的
C．若cos<O，则必为第二或第三象限角
D．函数
是周期为的偶函数
10．关于函数的奇偶性，有如下几种说法：
说法一：因为
＝
＝
是偶函数，故原函数是偶函数；
说法二：因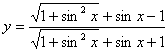
的分子分母同乘以
后变为
是奇函数，故原函数是奇函数；
说法三：因为
＝
＝
＝
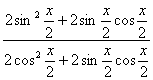是奇函数，故原函数是奇函数．
下列判断正确的是（ ）
A．三种说法都正确
B．三种说法都有毛病，导致结论错了一个
C．三种说法都有毛病，导致结论错了两个
D．三种说法都有毛病，导致结论全错
11．如果函数y=sin2x+acos2x的图象关于直线
对称，那么a的值为（ ）
A．
B．- C．1 D．-1
12．要使函数
的值
在区间[a，a+3]上出现的次数不少于4次，不多于8次(a∈R)，则k的值是(
)
A．2 B．3 c．45 D．2或3
第Ⅱ卷(非选择题共90分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（本大题共4小题，每小题4分，共16分）
13．已知
，
，则
的值为
．
14．函数
的图象可由函数
的图象向 平移 个单位而得到．
15．已知
，且
，则、
的值分别为
。
16．已知
，则
的取值范围是 ．
三、解答题(本大题共6小题，计74分)
17．(本题满分12分)若
，求
与
的值．
18．(本题满分12分)已知函数
图象的一个最高点为(2，)，由该最高点到相邻最低点间的曲线与x交于点(6，O)．
(1)求这个函数的表达式； (2)求该函数的频率、初相和单调区间．
19．(本题满分12分)求函数
的递增区间。
20．(本题满分12分)已知
，且
，＋
。当
取最大值时，求
的值．
21．本题满分12分)已知、为锐角，
，
，求
的值．
22．(本题满分14分)
(1)已知周期函数为奇函数，且它的一个周期为3，f(0.4)＝-1，求f(11.6)的值；
(2)若f(x)=
的最小值为-6，求
的值；
(3)设
,函数
的最大值为
，求的值．
参考答案
