三角函数测试题
班级 姓名 得分 .
一、选择题：
1、
=…………………………………………………………………………………………( )
(A)
(B)－ (C)
(D) －
2、
弧度的圆心角所对弦长为2，则这个圆心角所夹扇形的面积为……………………………( )
(A)
(B) (C)
(D)
3、在（0，2
）内，满足sinx>cosx的角x的取值范围是…………………………………………( )
(A)(
，
) (B)(,
)∪(,) (C）(,) （D）(,)∪(,
)
4、已知
，则
=……………………………………………( )
(A)
（B）－
（C）－
（D）
5、已知函数
，则使得
恒成立的最小正整数C=…………（ ）
(A)1 (B)2 (C)3 (D) 4
6、设A、B都是锐角，cosA>sinB，则A＋B的取值范围是………………………………………（ ）
(A)
(，) (B) (0，)
(C) (0,)
(D) (,)
7、下列各式中，值为的是…………………………………………………………………………（ ）
(A)
(B)
(C)
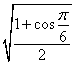(D) 
8、在适合条件
，x可以表示为……………………………………………（ ）
(A)
(B) － (C) ＋ (D)
－
9、要得到函数
的图象，只要将函数y=sin2x的图象……………………………（ ）
(A)左平移
(B)右平移
(C) 左平移
(D) 右平移
10、在△ABC中，
，则角B=…………………………………………………（ ）
(A) (B) (C) (D)
11、函数
具有性质……………………………………………………（ ）
(A)图象关于点（，0）对称，最大值为
(B) 图象关于点（，0）对称，最大值为1
(C)图象关于直线x=对称，最大值为 (D) 图象关于直线x=对称，最大值为1
12、函数y=
满足
=－，
=－，则适合条件的函数是………（ ）
(A) =sinx (B) =sin2x (C) =
(D) =sin2x＋cos2x
二、填空题：
13、角x的终边经过点（－1，－
），则sinx=
；
14、已知
，则
=
；
15、
=
；
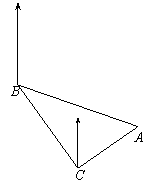
16、如图，货轮在海上以40km/h的速度沿着方位角（从正北方向顺时针转到目标方向）为140
的方向航行，为了确定船位，在B点观测灯塔A的方位角为110，航行半小时后到达C点，观察灯塔A的方位角为65，则货轮到达C点与A点的距离为 。
三、解答题：
17、已知
，求
。
18、若关于x的方程
有两个相等实数根。
⑴求实数a的取值范围；
⑵当a=
时，求
之值。
19、已知函数=
⑴求此函数的最小正周期；
⑵确定的单调递增区间；
⑶当取得最大值时，求x的集合。
20、某港口水深y（米）是时间t（0≤t≤24，单位：小时）的函数，记为y=
，下面是某日水深数据：
| t（时） | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y（米） | 10.0 | 13.0 | 10.01 | 7.0 | 10.0 | 13.0 | 10.01 | 7.0 | 10.0 |
经过长期观察，y=的曲线可以近似看成y=Asin
t+b的图象.
⑴根据以上数据求出y=的近似表达式；
⑵船底离海底5米或者5米以上是安全的，某船的吃水深度为6.5米（船底离水面距离），如果此船希望在同一天安全进出港，那么此船最多在港口停留多少时间？（忽略进出时间）.
21、（本题满分12分）已知电流I与时间t的函数关系式为I=
。
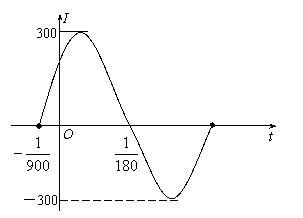
⑴右图是I=（
>0,
<）在一个周期内的图象，根据图中数据求I= 的解析式；
⑵如果t在任意一段
秒的时间内，电流I=都能取得一个最大值和最小值，那么的最小正整数是多少？