(高三年级数学第二次诊断测试)
本卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟。
第Ⅰ卷(选择题共60分)
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(![]() )=P(A)
)=P(A)![]() P(B)
P(B)
如果事件A在一次试验中发生的概率为p,那么n次独立重复试验中恰好发生k次的概率:![]() .
.
球体的体积公式:![]() (其中R 表示球的半径).
(其中R 表示球的半径).
一.选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的)
1.若抛物线![]() 上一点M的横坐标为4,M到焦点的距离为5,则点M到x轴的距离是 ( )
上一点M的横坐标为4,M到焦点的距离为5,则点M到x轴的距离是 ( )
A.![]() B.1
B.1
C.2 D.4
2.球的表面积与其内接正方体的表面积之比是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.函数![]() 的图像的对称轴方程是( )
的图像的对称轴方程是( )
A.x=1 B.x=2 C.x=3 D.x=-1
4.从x轴上一点引园![]() 的两条切线,其中一条切线的斜率为
的两条切线,其中一条切线的斜率为![]() ,则两切线夹角的正切值是( )
,则两切线夹角的正切值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.
![]()
5.函数![]() 的值域是( )
的值域是( )
A.{1} B.{-1,1} C.(-1,1) D.[-1,1]
6.已知![]() 都是正数,且
都是正数,且![]() ,则
,则![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知圆周上有10个等分点,以其三个点为顶点构成三角形,其中直角三角形的概率是( )
A.![]() B.
B. ![]()
C.![]() D.
D.![]()
8.已知![]() 是等差数列
是等差数列![]() 的前n项和,
的前n项和,![]() ,则
,则![]() ( )
( )
A. -7
B. ![]()
C. -10 D. 2
9.已知![]() ,则下列
,则下列![]() 值中能使△ABC是直角三角形的一个值是( )
值中能使△ABC是直角三角形的一个值是( )
A.![]() B.
B.![]() C.
C.![]() D.-5
D.-5
10.在正三棱柱![]() 中,
中,![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成的角的大小是( )
所成的角的大小是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.若关于x的方程![]() 有实根,则实数
有实根,则实数![]() 的取值范围是( )
的取值范围是( )
A. [-2,+∞) B.[2,2] C.[-2,2] D.![]()
12.已知![]() 为双曲线的左、右焦点,以双曲线左支上任意一点P为圆心、
为双曲线的左、右焦点,以双曲线左支上任意一点P为圆心、![]() 为半径的圆与以
为半径的圆与以![]() 为圆心、
为圆心、![]() 为半径的圆相切,则双曲线两渐近线的夹角是( )
为半径的圆相切,则双曲线两渐近线的夹角是( )
A. ![]() B.
B.![]() C.
C.![]() D.
D. ![]()
数 学(三)
第Ⅱ卷(非选择题共90分)
二.填空题(本大题共4小题,每小题4分,共16分。把答案填在题中横线上)
13.已知![]() 为一次函数,若
为一次函数,若![]() ,且
,且![]() 成等比数列,则
成等比数列,则
![]() 的值是______ .
的值是______ .
14.![]()
![]() 展开式中x的一次项的系数是 .
展开式中x的一次项的系数是 .
15.函数![]() 在
在![]() 上的最小值是 .
上的最小值是 .
16.函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,则
,则![]() 的最大值是________.
的最大值是________.
三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或或演算步骤)
17.(本小题满分12分)
已知函数![]()
![]() .
.
(1)写出此函数![]() 在R上的单调区间;
在R上的单调区间;
(2)若函数![]() 的图像与
的图像与![]() 的图像相切于相异的两点,求
的图像相切于相异的两点,求![]() 的值.
的值.
18.(本小题满分12分)
已知![]() ,回答以下问题:
,回答以下问题:
Ⅰ.若![]() ,求
,求![]() 的取值范围;
的取值范围;
Ⅱ.将![]() 用
用![]() 表示;
表示;
Ⅲ.求![]() 的最大值与最小值.
的最大值与最小值.
19.(本小题满分12分)
(文科)如图,在棱长为1的正方体![]() 中,
中,![]() 分别是
分别是![]() 的中点.
的中点.
(Ⅰ)求证:![]() 共面;
共面;
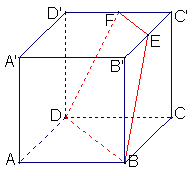 (Ⅱ)求点
(Ⅱ)求点![]() 到平面
到平面![]() 的距离;
的距离;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
(理科)如图,在棱长为1的正方体![]() 中,过
中,过![]() 及
及![]() 的中点
的中点![]() 作截面
作截面![]() 交
交![]() 于
于![]() .
.
(Ⅰ)求截面![]() 与底面
与底面![]() 所成角的大小;
所成角的大小;
(Ⅱ)求四棱锥![]() -
-![]() 的体积;
的体积;
(Ⅲ)求直线![]() 与截面
与截面![]() 所成角的大小.
所成角的大小.
20.(本小题满分12分)
某工厂统计资料显示,产品次品率![]() 与日产量
与日产量![]() (
(![]() ∈
∈![]() )的关系如下表:
)的关系如下表:
| 日产量 | 1 | 2 | 3 | 4 | … | 97 | 98 | 99 | 100 |
| 次品率 |
|
|
|
| … |
|
|
| 1 |
又生产一件正品能够盈利![]() 元,生产一件次品损失
元,生产一件次品损失![]() 元.
元.
(1)将该厂的日盈利额![]() (元)表示为日生产量
(元)表示为日生产量![]() 的函数;
的函数;
(2)为了获得最大盈利,该厂的日产量应定为多少件?
21. (本小题满分12分)
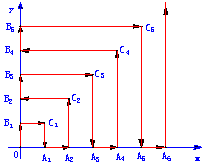
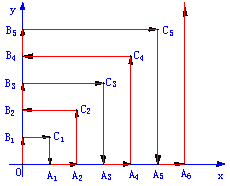
如图,一粒子在区域![]() 上运动,在第一秒内它从原点运动到点
上运动,在第一秒内它从原点运动到点![]() ,接着按图中箭头所示方向在x轴、y轴及其平行方向上运动,且每秒移动一个单位长度。
,接着按图中箭头所示方向在x轴、y轴及其平行方向上运动,且每秒移动一个单位长度。
(1)设粒子从原点到达点![]() 时,所经过的时间分别为
时,所经过的时间分别为![]() ,试写出
,试写出![]() 的通相公式;
的通相公式;
(2)(文科)求粒子从原点运动到点![]() 时所需的时间。
时所需的时间。
(理科)粒子从原点开始运动,求经过2004秒后,它所处的坐标。
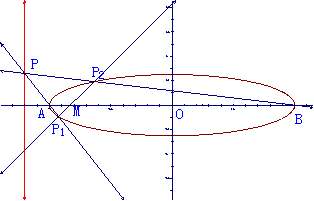
22.(本小题满分14分)
设![]() 是单位圆
是单位圆![]() 的直径,
的直径,![]() 是圆上的动点,过点
是圆上的动点,过点![]() 的切线与过点
的切线与过点![]() 的切线分别交于
的切线分别交于![]() 两点。四边形
两点。四边形![]() 的对角线
的对角线![]() 和
和![]() 的交点为
的交点为![]() .
.
(文科)求![]() 的轨迹。
的轨迹。
 (理科)过直径
(理科)过直径![]() 上一定点
上一定点![]() (异与
(异与![]() 三点)作直线
三点)作直线![]() ,
,![]() 与
与![]() 的轨迹交于
的轨迹交于![]() 两点。求证两条动直线
两点。求证两条动直线![]() 与
与![]() 的交点
的交点![]() 在垂直于
在垂直于![]() 的直线上。
的直线上。
2004年高考模拟试题
数 学(三)
(高三年级第二次诊断测试)
参考答案
一、选择题(每小题5分,满分60分)
1.D . 由抛物线![]() 上一点M的横坐标为4,M到焦点的距离为5,得
上一点M的横坐标为4,M到焦点的距离为5,得![]()
![]() ,即点M到x轴的距离是4.
,即点M到x轴的距离是4.
2.C. 设球的半径为R, 球内接正方体的棱长为a,则![]() 。球的表面积与其内接正方体的表面积之比是
。球的表面积与其内接正方体的表面积之比是![]() .
.
3.A. 函数![]() 的图像的对称轴方程就是
的图像的对称轴方程就是![]() 的对称轴x=1.
的对称轴x=1.
4.C.从x轴上一点引园![]() 的两条切线,其中一条切线的斜率为
的两条切线,其中一条切线的斜率为![]() ,另一条就是x轴,所以这两切线夹角的正切值是
,另一条就是x轴,所以这两切线夹角的正切值是![]() .
.
5.D.由函数![]() ,
,
当![]() 的终边在第一象限时,
的终边在第一象限时,![]() ;
;
当![]() 的终边在第二象限时,
的终边在第二象限时,![]()
![]() ;
;
当![]() 的终边在第三象限时,
的终边在第三象限时,![]() ;
;
当![]() 的终边在第四象限时,
的终边在第四象限时,![]()
![]() ;
;
当![]() 的终边在两个坐标轴上时,
的终边在两个坐标轴上时,![]() ;
;
综上述![]() 的值域是 [-1,1] .
的值域是 [-1,1] .
6.A. 由![]() 都是正数,且
都是正数,且![]()
![]()
![]()
![]()
![]()
![]() .
.
7.B. 圆周上10个等分点,恰好构成5条直径,要以其三个点为顶点构成三角形![]() 个,其中直角三角形有
个,其中直角三角形有![]() 个。概率是
个。概率是![]() .
.
8.A.由![]() 得,
得,![]() ,
,![]() 则
则![]() ,
,![]()
![]()
=![]() .
.
9.C. 若![]() 垂直,则
垂直,则![]() ,四个答案都不符合;若
,四个答案都不符合;若![]() 与
与![]() 垂直,则
垂直,则![]()
![]() ,C符合.
,C符合.
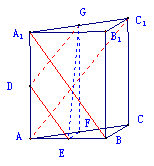 10.C.在正三棱柱
10.C.在正三棱柱![]() 中,不妨设AB=2, 则
中,不妨设AB=2, 则![]() =2
=2![]() ,如图所示D、E、F、G为对应线段的中点,异面直线
,如图所示D、E、F、G为对应线段的中点,异面直线![]() 与
与![]() 所成的角就是DE与DG所成的角,DE=DG=
所成的角就是DE与DG所成的角,DE=DG=![]() ,EG=3,由余弦定理得
,EG=3,由余弦定理得![]() ,从而异面直线
,从而异面直线![]() 与
与![]() 所成的角就是的大小是
所成的角就是的大小是![]() .
.
11.D. 若关于x的方程![]() 有实根,等价于求函数
有实根,等价于求函数![]() 得值域,由于
得值域,由于![]() 则实数
则实数![]() 的取值范围是
的取值范围是![]() .
.
12.B.以双曲线左支上任意一点P为圆心、![]() 为半径的圆与以
为半径的圆与以![]() 为圆心、
为圆心、![]() 为半径的圆相切,则
为半径的圆相切,则![]()
![]()
![]()
![]() ,所以双曲线两渐近线的夹角是
,所以双曲线两渐近线的夹角是![]() .
.
二、填空题(每小题4分,满分16分)
13.10000. 设![]() ,
,![]() ,由
,由![]() 成等比数列
成等比数列
![]() ,可得
,可得![]() 则
则![]()
=![]()
![]() .
.
14.![]() .
.![]()
![]() 展开式中x的一次项的系数是
展开式中x的一次项的系数是
![]() .
.
 15.
15.![]() .令
.令![]() ,函数
,函数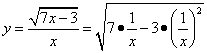
![]() 在
在![]() 的两个端点处打到最小值
的两个端点处打到最小值![]() .
.
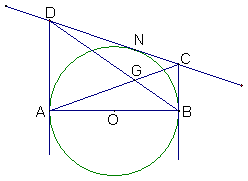
16.![]() .如图,要使函数
.如图,要使函数![]() 在定义域
在定义域![]() 上,值域为
上,值域为![]() ,则
,则![]() 的最大值是
的最大值是![]() .
.
三、解答题(本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤)
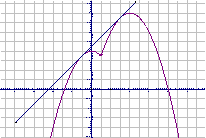 17.解:(1)∵
17.解:(1)∵![]() =
=
![]() .
.
∴![]()
![]()
∴函数![]() 在区间(-∞,0
在区间(-∞,0![]() ,
,![]() 上是增函数,在区间
上是增函数,在区间![]() ,[2,+∞
,[2,+∞![]() 上是减函数; …………(6分)
上是减函数; …………(6分)
(2)由函数![]() 的图像与
的图像与![]() 的图像相切于相异的两点,得
的图像相切于相异的两点,得
![]() 的判别式
的判别式![]()
且![]() 的判别式
的判别式![]() …………(10分)
…………(10分)
所以求![]() .
…………(12分)
.
…………(12分)
18.解:(1)因为![]() ,所以
,所以![]()
所以![]() ,
,
故![]() 的取值范围是
的取值范围是![]() ……………(4分)
……………(4分)
(2)![]()
![]() ,
,![]()
![]() ;……(8分)
;……(8分)
(3)![]() =
=![]()
=![]()
=![]() =
=![]()
设![]() ,
,![]()
![]()
因为![]()
![]() 时,
时,![]() , 所以
, 所以![]() 在
在 ![]() 上为减函数,
上为减函数,
所以![]() ,
,![]()
即![]() 的最大值是1,最小值是
的最大值是1,最小值是![]() . ………………………(12分)
. ………………………(12分)
 19. (文科)如图,,
19. (文科)如图,,
(Ⅰ)证明:在棱长为1的正方体![]() 中,由
中,由![]() 得
得![]() ,又因为
,又因为![]() 分别是
分别是![]() 的中点,所以
的中点,所以![]() ,于是
,于是![]() ,即
,即![]() 共面;
共面;
……(4分)
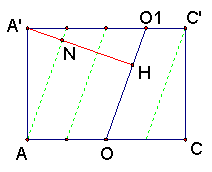 (Ⅱ)解:在棱长为1的正方体
(Ⅱ)解:在棱长为1的正方体![]() 中,连结
中,连结![]() ,因为
,因为![]() ,所以平面
,所以平面![]() ,其交线为
,其交线为![]() ,过
,过![]() 作交线为
作交线为![]() 的垂线
的垂线![]() ,垂足为H,
,垂足为H,![]() 的长就是求点
的长就是求点![]() 到平面
到平面![]() 的距离,
的距离,
如图![]() =
=
故点![]() 到平面
到平面![]() 的距离是1; ……………(8分)
的距离是1; ……………(8分)
(Ⅲ)解:连接![]() ,
,![]() ,由(Ⅱ)
,由(Ⅱ)![]() 就是
就是![]() 在平面
在平面![]() 上的射影,
上的射影,![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成角,且
所成角,且![]() =1,
=1,![]() =
=![]() ,所以
,所以![]() ,
,
从而,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
…(12分)
.
…(12分)
(理科)(Ⅰ)解:在棱长为1的正方体![]() 中,连结
中,连结![]() ,因为
,因为![]() ,所以平面
,所以平面![]() ,其交线为
,其交线为![]() ,再过
,再过![]() 作垂直于底面的垂线交
作垂直于底面的垂线交![]() 于
于![]() ,则
,则![]() 就是截面
就是截面![]() 与底面
与底面![]() 所成角,由题意得,
所成角,由题意得,![]() ,所以
,所以
故截面![]() 与底面
与底面![]() 所成角为
所成角为![]() ;……4分
;……4分
(Ⅱ)解:同(文)(Ⅱ)点![]() 到平面
到平面![]() 的距离是1,
的距离是1,
由上面![]() ,得
,得![]() ,
,
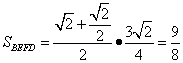 ,
,
四棱锥![]() -
-![]() 的体积
的体积![]() ; ……8分
; ……8分
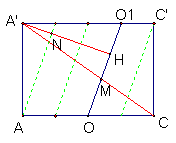
(Ⅲ)解:连接![]() 交
交![]() 于M,则
于M,则![]() 就是直线
就是直线![]() 与截面
与截面![]() 所成角,
所成角,
 由
由![]() =1,
=1,![]() ,
,
得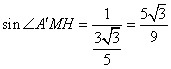 ,
,
故直线![]() 与截面
与截面![]() 所成角为
所成角为![]() .……12分
.……12分
20.(本小题满分12分)
(1)解:设日产量为x(![]() ,
,![]() ∈
∈![]() ),则次品率
),则次品率![]() =
=![]() ,次品数为xp,正品数为x-xp,依题意
,次品数为xp,正品数为x-xp,依题意
![]() =
=![]() ,(
,(![]() ,
,![]() ∈
∈![]() ) ……6分
) ……6分
(2)解:![]()
![]() =
=![]()
![]()
当![]() 时,
时,![]() 取最大值。……10分
取最大值。……10分
因为![]() ∈
∈![]() ,可以判断当x=89时,
,可以判断当x=89时,![]() 取最大值。
取最大值。
所以,为了获得最大盈利,该厂的日产量应定为89件。……12分
21.(1)解: 设![]() ,当粒子从原点到达
,当粒子从原点到达![]() 时,显然有
时,显然有
![]()
![]()
![]()
![]()
![]()
![]()
……… ………
![]()
![]() .………2分
.………2分
∴![]() =
=![]()
![]() ………4分
………4分
![]()
![]()
![]()
![]()
即![]() ………7分
………7分
(2)(文科)有图形知,粒子从原点运动到点![]() 时所需的时间是到达点
时所需的时间是到达点![]() 所经过得时间
所经过得时间![]() 再加(44-16)=28秒,所以
再加(44-16)=28秒,所以![]() 秒。………12分
秒。………12分
(理科)由![]()
![]() 2004,解得
2004,解得![]() ,取最大得n=44,
,取最大得n=44,
计算得![]() =1980<2004,所以粒子从原点开始运动,经过1980秒后到达点
=1980<2004,所以粒子从原点开始运动,经过1980秒后到达点![]() ,再向左运行24秒所到达的点的坐标为(20,44)。………12分
,再向左运行24秒所到达的点的坐标为(20,44)。………12分
22.(本小题满分14分)
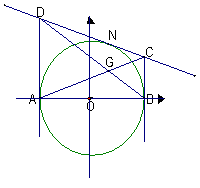 解:(文科) 以圆心O为原点,直径
解:(文科) 以圆心O为原点,直径![]() 为x轴建立直角坐标系,则A(-1,0),B(1,0),单位圆的方程为
为x轴建立直角坐标系,则A(-1,0),B(1,0),单位圆的方程为![]() 设 N的坐标为
设 N的坐标为![]() ,则切线DC的方程为:
,则切线DC的方程为:![]() ,
………4分
,
………4分
由此可得![]()
AC的方程为
![]()
BD的方程为
![]() ………8分
………8分
将两式相乘得:![]() ,即
,即![]()
当点N恰为A或B时,四边形![]() 变为线段AB,这不符合题意,所以轨迹不能包括A、B两点,所以
变为线段AB,这不符合题意,所以轨迹不能包括A、B两点,所以![]() 的轨迹方程为
的轨迹方程为![]() ,(
,(![]() )。………14分
)。………14分
另法:设四边形![]() 的对角线
的对角线![]() 和
和![]() 的交点为
的交点为![]() 的坐标为(u,v).
的坐标为(u,v).
则AG的方程为![]() 与切线BC的交点为C(1,
与切线BC的交点为C(1,![]() );
);
BG的方程为![]() 与切线AD的交点为D(-1,
与切线AD的交点为D(-1,![]() )。
)。
所以,经过C(1,![]() )、D(-1,
)、D(-1,![]() )的直线DC的方程为:
)的直线DC的方程为:![]() ,
,
即![]()
由于DC与单位圆相切,所以原点O到DC的距离为1,从而有![]()
整理得 ![]() ,也就是
,也就是![]() 的轨迹方程为
的轨迹方程为![]() 。
。
当点N恰为A或B时,四边形![]() 变为线段AB,这不符合题意,所以轨迹不能包括A、B两点,所以
变为线段AB,这不符合题意,所以轨迹不能包括A、B两点,所以![]() 的轨迹方程为
的轨迹方程为![]() ,(
,(![]() )。
)。
(理科)同(文科)可求出![]() 的轨迹方程为
的轨迹方程为![]() ,(
,(![]() )………8分
)………8分
设过直径![]() 上一定点
上一定点![]() (m,0)(异与
(m,0)(异与![]() 三点)作直线
三点)作直线![]() ,
,![]() 与
与![]() 的轨迹交于
的轨迹交于
![]() 两点。两条动直线
两点。两条动直线![]() 与
与![]() 的交点
的交点![]() 。
。
则AP的方程为![]() 交
交![]() 的轨迹
的轨迹![]() (
(![]() )于
)于
![]() ………10分
………10分
BP的方程为![]() 交
交![]() 的轨迹
的轨迹![]() (
(![]() )于
)于
![]() ………12分
………12分
因为点![]() (m,0)、
(m,0)、![]() 三点共线,则
三点共线,则![]() ,整理并化简得
,整理并化简得![]() ,
,
即点p得轨迹方程为![]() ,也就是点P在垂直于
,也就是点P在垂直于![]() 的直线上。………14分
的直线上。………14分