三角函数与向量练习(一)
1、将函数y=f(x)·sinx的图象向右平移![]() 个单位后,再作关于x轴的对称变换得到函数
个单位后,再作关于x轴的对称变换得到函数
y=-cos2x的图象.则f(x)可以是 ( )
A.-2sinx B.2sinx C.-2cosx D.2cosx
2、已知![]() 、
、![]() 为两个非零向量,有以下命题:①
为两个非零向量,有以下命题:①![]() =
=![]() ,②
,②![]() ·
·![]() =
=![]() ,③
,③![]() =
=![]() 且
且
![]() ∥
∥![]() .其中可以作为
.其中可以作为![]() =
=![]() 的必要但不充分条件的命题是 ( )
的必要但不充分条件的命题是 ( )
A.② B.①③ C.②③ D.①②③
3、抛物线y2=2x与过焦点的直线交于A、B两点,O是坐标原点,则![]() 等于( )
等于( )
A.-![]() B.
B.![]() C.-3 D.3
C.-3 D.3
4、已知命题p:函数![]() 的值域为R.命题q:函数
的值域为R.命题q:函数![]()
是减函数.若p或q为真命题,p且q为假命题,则实数a的取值范围是 ( )
A.a≤1 B.a<2 C.1<a<2 D.a≤1或a≥2
5、已知 a =2 sin15°, b =4 cos15°,a与b的夹角为30°,则a·b为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6、若![]() 的值是 ( )
的值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、下列命题中:①![]() ∥
∥![]()
![]() 存在唯一的实数
存在唯一的实数![]() ,使得
,使得![]() ;②
;②![]() 为单位向量,
为单位向量,
且![]() ∥
∥![]() ,则
,则![]() =±
=±![]() ·
·![]() ;③
;③![]() ;④
;④![]() 与
与![]() 共线,
共线,![]() 与
与![]() 共线,则
共线,则![]() 与
与![]() 共线;⑤若
共线;⑤若![]() ,其中正确命题的序号是 ( )
,其中正确命题的序号是 ( )
A.①⑤ B.②③ C.②③④ D.①④⑤
8、在△ABC中,角A、B、C所对的边分别是a、b、c,且A、B、C成等差a、b、c成等比,那么△ABC一定是 ( )
A.直角三角形 B.等腰直角三角形 C.等边三角形 D.钝角三角形
9、函数y=sin2x+2cosx(![]() )的最大值与最小值分别为 ( )
)的最大值与最小值分别为 ( )
A.最大值![]() ,最小值为-
,最小值为-![]() B.最大值为
B.最大值为![]() ,最小值为-2
,最小值为-2
C.最大值为2,最小值为-![]() D.最大值为2,最小值为-2
D.最大值为2,最小值为-2
10、关于函数![]() ,有下列命题
,有下列命题
①由![]() 的整数倍;②
的整数倍;②![]() 的表达式可改写为
的表达式可改写为
![]() ;③
;③![]() 的图象关于点
的图象关于点![]() 对称;④
对称;④![]() 的图象关于直线
的图象关于直线
![]() 对称;其中正确命题的序号是 ( )
对称;其中正确命题的序号是 ( )
A.①② B.②③ C.①③ D.②④
11、要得到函数![]() 的图象,可将
的图象,可将![]() 的图象 ( )
的图象 ( )
A.向左平移![]() 个单位 B.向右平移
个单位 B.向右平移![]() 个单位C向左平移
个单位C向左平移![]() 个单位D.向右平移
个单位D.向右平移![]() 个单位
个单位
12、使![]() 为奇函数,且在
为奇函数,且在![]() 上是减函数的
上是减函数的![]() 的一个值是 ( )A.
的一个值是 ( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13、函数![]() 的最大值是 ( )
的最大值是 ( )
A.![]() B.
B.![]() C.3 D.2
C.3 D.2
14、设a、b是方程![]() 的两个不相等的实数根,那么过点A(a,a2)和
的两个不相等的实数根,那么过点A(a,a2)和
B(b,b2)的直线与圆![]() 的位置关系是 ( )
的位置关系是 ( )
A.相离 B.相切 C.相交 D.随θ的值变化而变化
15、给定两个向量![]() ,则x的等于 ( )
,则x的等于 ( )
A.-3 B.![]() C.3 D.-
C.3 D.-![]()
16、函数![]() 的单调递增区间是
.
的单调递增区间是
.
17、将抛物线![]() 按向量
按向量![]() =(4,-3)平移后所得抛物线的焦点坐标为 .
=(4,-3)平移后所得抛物线的焦点坐标为 .
18、△ABC中,若![]() 的值为
.
的值为
.
19、已知![]() 与
与![]() 的夹角为60°,则
的夹角为60°,则![]() 与
与![]() -
-![]() 的夹角余弦为 .
的夹角余弦为 .
20、过双曲线![]() 的右焦点F(c,0)的直线交双曲线于M、N两点,交y轴于P
的右焦点F(c,0)的直线交双曲线于M、N两点,交y轴于P
点,则有![]() 的定值为
的定值为![]() 类比双曲线这一结论,在椭圆
类比双曲线这一结论,在椭圆![]()
(a>b>0)中,![]() 是定值
.
是定值
.
21、已知![]() 是锐角,
是锐角,![]() 且满足
且满足![]()
(1)求证:![]() ;(2)当
;(2)当![]() 取最大值时,求
取最大值时,求![]() 的值。
的值。
三角函数与向量练习(二)
1、O是平面上一定点,A、B、C是平面上不共线的三点,动点P满足![]()
![]() ,则P的轨迹一定通过△ABC的 ( )
,则P的轨迹一定通过△ABC的 ( )
A.外心 B.重心 C.内心 D.垂心
2、函数![]() ,给出下述命题:①
,给出下述命题:①![]() 有最小值;②当
有最小值;②当
![]() 的值域为R;③当
的值域为R;③当![]() 上有反函数,则其中正确的命题是
上有反函数,则其中正确的命题是
A.①②③ B.②③ C.①② D.①③
3、把直线![]() 按向量
按向量![]() 平移后,所得直线与圆
平移后,所得直线与圆![]() 相
相
切,则实数![]() 的值为 ( )
的值为 ( )
A.39 B.13 C.-21 D.-39
4、已知![]() ,则下列结论中正确的是 ( )
,则下列结论中正确的是 ( )
A.函数![]() 的周期是
的周期是![]() . B.函数
. B.函数![]() 的最大值为1.
的最大值为1.
C.将![]() 的 图象向左平移
的 图象向左平移![]() 单位后得
单位后得![]() 的图象.
的图象.
D.将![]() 的 图象向右平移
的 图象向右平移![]() 单位后得
单位后得![]() 的图象.
的图象.
5、若![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6、已知A、B、C、D是坐标平面上不共线的四点,则![]() 共线是
共线是![]() =0
=0
的什么条件 ( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
7、已知向量![]() 的值是 ( )
的值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
8、设F1,F2是双曲线![]() 的两个焦点,点P在双曲线上,且
的两个焦点,点P在双曲线上,且![]() ,
,
则![]() 的值等于( )A.2 B.
的值等于( )A.2 B.![]() C.4 D.8
C.4 D.8
9、已知O、A、B三点的坐标分别为O(0,0),A(3,0),B(0,3),点P在线段AB上,且![]() 的最大值为( )
的最大值为( )
A.3 B.6 C.9 D.12
10、已知函数f(x)=1-2sin2ωx的最小正周期是函数g(x)=sin4x的最小正周期的2倍,则ω= A.![]() B.1 C.2
D.4
B.1 C.2
D.4
11、函数y
=cos2x的图象,可由y=cos(2x-![]() 的图象,经过下列哪种平移变
的图象,经过下列哪种平移变
换得到(
) A.向左平移![]() 个单位 B.向右平移
个单位 B.向右平移![]() 个单位
个单位
C. 向左平移![]() 个单位
D.向右平移
个单位
D.向右平移![]() 个单位
个单位
12、若函数![]() 的表达式是( )A.
的表达式是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13、函数![]() 取最大值时x的值为 ( )
取最大值时x的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14、已知△ABC中,点D在BC边上,且![]() 则
则![]() 的值是( )A.
的值是( )A.![]() B.
B.![]() C.-3 D.0
C.-3 D.0
15、已知i , j为互相垂直的单位向量,![]() 的夹角为锐角,则实数
的夹角为锐角,则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
16、把点A(2,1)按向量![]() =(-2,3)平移到B,此时点B分向量
=(-2,3)平移到B,此时点B分向量![]() (O为坐标原点)的比为-2,则C点的坐标为
.
(O为坐标原点)的比为-2,则C点的坐标为
.
17、把120个相同的小球紧密地垒成一个正三棱锥,那么最低一层有 个小球.
18、设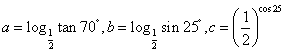 ,则
,则![]() 的大小关系为
.
的大小关系为
.
19、已知![]() .
.
20、已知点A(2,0),B(4,0),动点P在抛物线![]() 运动,则使
运动,则使![]() 取得最小值的点P的坐标是
.
取得最小值的点P的坐标是
.
21、如果函数f(x)在区间D上满足,对区间D上的任意x1,x2,…,xn,有:![]() 则称f(x)在区间D为凸函数,
则称f(x)在区间D为凸函数,
已知:y =sinx在区间(0,![]() )上是凸函数,那么在ΔABC中,sinA+sinB+sinC
)上是凸函数,那么在ΔABC中,sinA+sinB+sinC
的最大值为 A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
22、函数![]() 的图象的相邻两支截直线
的图象的相邻两支截直线![]() 所得线段长为
所得线段长为![]() 的值是 A.0 B.-1 C.1 D.
的值是 A.0 B.-1 C.1 D.![]()
三角函数与向量练习(三)
1、设![]() 为坐标平面内一点,O为坐标原点,记f(x)=OM,当x变化时,函数 f(x)的最小正周期是 ( )
为坐标平面内一点,O为坐标原点,记f(x)=OM,当x变化时,函数 f(x)的最小正周期是 ( )
A.30π B.15π C.30 D.15
2、(理科)设△ABC的两个内角A,B所对的边分别为a , b,复数![]() 若复数z1·z2在复平面上对应的点在虚轴上,则△ABC是 ( )
若复数z1·z2在复平面上对应的点在虚轴上,则△ABC是 ( )
A.等腰三角形或直角三角形B.等腰直角三角形C.等腰三角形 D.直角三角形
(文科)函数![]() 有且只有一个实根,那么实数a应满足( )
有且只有一个实根,那么实数a应满足( )
A.a<0 B.0<a<1 C.a=0 D.a>1
3、设向量![]() ( )
( )
A.![]() B.
B.![]() C.-
C.-![]() D.-
D.-![]()
4、已知θ∈R,则直线![]() 的倾斜角的取值范围是 ( )
的倾斜角的取值范围是 ( )
A.[0°,30°] B.![]() C.[0°,30°]∪
C.[0°,30°]∪![]() D.[30°,150°]
D.[30°,150°]
5、已知两点M(-2,0),N(2,0),点P满足![]() =12,则点P的轨迹方程为( )
=12,则点P的轨迹方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6、一直角三角形三边长成等比数列,则 ( )A.三边长之比3:4:5
B.三边长之比为![]() C.较大锐角的正弦为
C.较大锐角的正弦为![]() D.较小锐角的正弦为
D.较小锐角的正弦为![]()
7、△ABC中,a、b、c成等比数列,则![]() 的值是 ( )
的值是 ( )
A.0 B.1 C.2 D.![]()
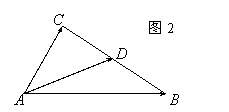
8、已知![]() 夹角为
夹角为![]() 如图2,若
如图2,若![]()
![]() ,且
,且![]() 为
为
![]() 中点,则
中点,则![]() 的长度为 ( )
的长度为 ( )
 A.
A.![]() B.
B.![]()
 C.7 D.8
C.7 D.8
9、已知△ABC的三个顶点的A、B、C及平面内一点P满足![]() ,下列结论中正确的是( )
,下列结论中正确的是( )
(A)P在△ABC内部 (B)P在△ABC外部
(C)P在AB边所在直线 (D)P是AC边的一个三等分点
10、已知点![]() ,
,![]() ,则直线AB的倾斜角为 ( )
,则直线AB的倾斜角为 ( )
A.36° B.54° C.144° D.126°
11、函数y=Asin(ωx+φ)(A>0,ω>0,φ<![]()
![]() 的图象如图所示,则y的表达式为( )
的图象如图所示,则y的表达式为( )
A.y=2sin(![]() ) B.y=2sin(
) B.y=2sin(![]() ) C.y=2sin(2x+
) C.y=2sin(2x+![]() ) D.y=2sin(2x-
) D.y=2sin(2x-![]() )
)
12、满足![]() ,BC=10的
,BC=10的![]() 恰好有不同两个,则边AB的长的取值范围为( )
恰好有不同两个,则边AB的长的取值范围为( )
A. (10, 20) B. (5, 10)
C.
![]() D.
D. ![]()
13、函数![]() ,对于任意的
,对于任意的![]() ,都有
,都有![]() ,则
,则![]() 的最小值为( )A.
的最小值为( )A.
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
14、A、B、C为任意三角形的内角,![]() ,
,![]() ,
,
![]() ,
,![]() ,其中恒为常数的是
( )
,其中恒为常数的是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
15、函数y=sin2x的图象按向量a平移后,所得函数的解析式是y=cos2x+1,则a等于( )A.(![]() ,1) B.(-
,1) B.(-![]() ,1) C. (-
,1) C. (-![]() ,1) D. (
,1) D. (![]() ,1)
,1)
16、已知a=(2,1) , b =(3,x), 若(2a-b)⊥b,则x的值为 ( )
A.3 B. -1 C.-1或3 D.-3或1
17、台风中心从A地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东40千米处,B城市处于危险区内的时间为 ( )
A. 0.5小时 B. 1小时 C. 1.5小时 D. 2小时
18、(文不作)已知![]() 且
且![]() 则
则![]() 的最小值
( )
的最小值
( )
A.等于-2 B.等于0 C.等于-4 D.不存在
19、(文不作)设复数![]() ,则满足等式
,则满足等式![]() 的复数
的复数![]() 对应的点的轨迹是( )
对应的点的轨迹是( )
A.圆 B.椭圆 C.双曲线 D.抛物线
20、在![]() 中,
中,![]() 分别为角A、B、C所对的边,且
分别为角A、B、C所对的边,且
![]() ,则
,则![]() =_____
=_____
21、在![]() 中,
中,![]() ,则
,则![]() =_______
=_______
22、设平面上有四个互异的点A、B、C、D,已知![]() ,则
,则![]() 的形状是______ 23、在△ABC中,AB =
1,BC = 2,则角C的取值范围是
的形状是______ 23、在△ABC中,AB =
1,BC = 2,则角C的取值范围是
24、已知![]() 则
则![]() 的取值范围是______________。
的取值范围是______________。
25、在△ABC中,角A,B,C所对的边分别为![]() ,且
,且![]() 依次成等比数列,求
依次成等比数列,求
![]() 的取值范围。
的取值范围。
26、在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南![]() 方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动. 台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大. 问几小时后该城市开始受到台风的侵袭?
方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动. 台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大. 问几小时后该城市开始受到台风的侵袭?
高考《三角函数与向量》专题复习
1、在下列四个命题中: ①函数y=tan(x+![]() )的定义域是 {x x ≠
)的定义域是 {x x ≠![]() + k
+ k![]() ,k∈Z};
,k∈Z};
②已知sinα =![]() ,且α∈[0,2
,且α∈[0,2![]() ],则α的取值集合是{
],则α的取值集合是{![]() } ;③函数
} ;③函数![]() 的最小正周期是
的最小正周期是![]() ;④△ABC中,cosA>cosB的充要条件是A<B;⑤函数
;④△ABC中,cosA>cosB的充要条件是A<B;⑤函数![]() 的最小值为
的最小值为![]() ,把你认为正确的命题的序号都填在横线上
.
,把你认为正确的命题的序号都填在横线上
.
2、若![]() .
.
3、同住一间寝室的四名女生,她们当中有一人在修指甲,一人在看书,一人在梳头发,另一人在听音乐。①A不在修指甲,也不在看书 ②B不在听音乐,也不在修指甲
③如果A不在听音乐,那么C不在修指甲④D既不在看书,也不在修指甲
⑤C不在看书,也不在听音乐,若上面的命题都是真命题,问她们各在做什么?
A在 ;B在 ;C在 ;D在 .
4、已知![]() 的值为_______
的值为_______
5、函数![]() 在
在![]() 上的最大值是
.(文不作)
上的最大值是
.(文不作)
6、求函数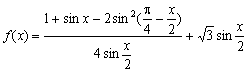 的最大值及取最大值时相应的x的集合.
的最大值及取最大值时相应的x的集合.
7、在![]() 中,内角A、B、C的对边分别为a、b、c,已知
中,内角A、B、C的对边分别为a、b、c,已知![]() ,
,![]() ,求角A的取值范围.
,求角A的取值范围.
8、(1)已知![]() =4,
=4,![]() =3,(2
=3,(2![]() -3
-3![]() )·(2
)·(2![]() +
+![]() )=61,求
)=61,求![]() 与
与![]() 的夹角θ;
的夹角θ;
(2)设![]() =(2,5),
=(2,5),![]() =(3,1),
=(3,1),![]() =(6,3),在
=(6,3),在![]() 上是否存在点M,使
上是否存在点M,使
![]() ,若存在,求出点M的坐标,若不存在,请说明理由.
,若存在,求出点M的坐标,若不存在,请说明理由.
9、已知函数![]() 、b为常数,且
、b为常数,且![]() )的图象过点(
)的图象过点(![]() ),且函数
),且函数![]() 的最大值为2.(1)求函数
的最大值为2.(1)求函数![]() 的解析式,并写出其单调递增区间;(2)若函数
的解析式,并写出其单调递增区间;(2)若函数![]() 的图象按向量
的图象按向量![]() 作移动距离最小的平移后,使所得的图象关于y轴对称,求出向量
作移动距离最小的平移后,使所得的图象关于y轴对称,求出向量![]() 的坐标及平移后的图象对应的函数解析式.
的坐标及平移后的图象对应的函数解析式.
10、已知曲线![]() ,直线l过A(a,0)、
,直线l过A(a,0)、
B(0,-b)两点,原点O到l的距离是![]() (Ⅰ)求双曲线的方程;(Ⅱ)过点B作
(Ⅰ)求双曲线的方程;(Ⅱ)过点B作
直线m交双曲线于M、N两点,若![]() ,求直线m的方程.
,求直线m的方程.
11、△ABC中,三个内角分别是A、B、C,向量![]()
![]() 时,求
时,求![]() .
.
12、已知点H(-6,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足![]() (1)当点P在y轴上移动时,求点M的轨迹C;(2)过点
(1)当点P在y轴上移动时,求点M的轨迹C;(2)过点
T(-2,0)作直线l与轨迹C交于A、B两点,若在x轴上存在一点![]() ,
,
使得△AEB是以点E为直角顶点的直角三角形,求直线l的斜率k的取值范围.
13、已知向量![]() =(2,2),向量
=(2,2),向量![]() 与向量
与向量![]() 的夹角为
的夹角为![]() ,且
,且![]() ·
·![]() =-2,(1)求向量
=-2,(1)求向量![]() ;
;
(2)若![]() ,其中A、C是△ABC的内角,若三角形的三内角A、B、C依次成等差数列,试求
,其中A、C是△ABC的内角,若三角形的三内角A、B、C依次成等差数列,试求![]() +
+![]() 的取值范围.
的取值范围.
14、已知函数![]() (Ⅰ)将f(x)写成
(Ⅰ)将f(x)写成![]() 的形式,并求其图象对称中心的横坐标;(Ⅱ)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
的形式,并求其图象对称中心的横坐标;(Ⅱ)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
15、如图:P(-3,0),点A在y轴上,点Q在x轴的正半轴上,且![]() 的延长线上取一点M,使
的延长线上取一点M,使![]() =2
=2![]() .
.
(I)当A点在y轴上移动时,求动点M的轨迹C的方程;
(II)已知![]() 为
为
方向向量的直线l与轨迹C交于E、F两点,又点D(1,0),若∠EDF为钝角时,求k的取值范围.
16、已知A、B、C的坐标分别为A(3,0),B(0,3),C(![]() ),
),![]()
(I)若![]() 求角
求角![]() 的值;(II)若
的值;(II)若![]() 的值.
的值.
17、已知△ABC中,![]() 且最长边的长度为1,
且最长边的长度为1,
求(1)角C的大小.(2)最短边的长.
18、已知向量![]() 向量
向量![]() 与向量
与向量![]() 夹角为
夹角为![]() ,且
,且![]() .(1)求向量
.(1)求向量![]() ;
;
(2)若向量![]() 与向量
与向量![]() =(1,0)的夹角为
=(1,0)的夹角为![]() ,其中A,C
,其中A,C
为△ABC的内角,且A,B,C依次成等差数列,试求求![]() +
+![]() 的取值范围.
的取值范围.
19、设△ABC的内角A,B,C成等差数列,且满足条件![]() 试判断△ABC的形状,并证明你的结论.
试判断△ABC的形状,并证明你的结论.
20、设![]() 为直角坐标平面内
为直角坐标平面内![]() 轴正方向上的单位向量,若向量
轴正方向上的单位向量,若向量![]() 且
且![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,设
两点,设![]() 是过点
是过点![]() 且以
且以![]() 为方向向量的直线上一动点,满足
为方向向量的直线上一动点,满足![]() (
(![]() 为坐标原点),问是否存在这样的直线
为坐标原点),问是否存在这样的直线![]() ,使得四边形
,使得四边形![]() 为矩形?若存在,求出直线
为矩形?若存在,求出直线![]() 的方程;若不存在,试说明理由.
的方程;若不存在,试说明理由.
8、解:(1)∵(2![]() -3
-3![]() )·(2
)·(2![]() +
+![]() )=61,∴
)=61,∴![]() …(2分)
…(2分)
又![]() =4,
=4,![]() =3,∴
=3,∴![]() ·
·![]() =-6.……(4分).
=-6.……(4分).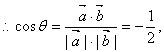 …………(5分)
…………(5分)
∴θ=120°.…(6分)(2)设存在点M,且![]()
![]()
![]() …(8分)
…(8分)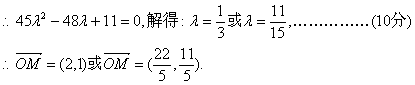
∴存在M(2,1)或![]() 满足题意.……………………(12分).
满足题意.……………………(12分).
9解:(1)
![]()
![]() ……2分
……2分
所以函数![]() 的解析式是
的解析式是![]() …3分
…3分
![]() 的单调递增区间是
的单调递增区间是![]() ………6分
………6分
(2)∵平移后的图象对应的函数解析式是![]() ………8分
………8分
图象关于y轴对称,即![]() 为偶函数,
为偶函数,
![]()
![]() 恒成立……9分
恒成立……9分
![]()
![]() ,……10分
,……10分
![]() ……11分
……11分
故![]()
![]() ,图象对应的函数解析式为
,图象对应的函数解析式为![]() …………12分
…………12分
(注:学生由作图观察得到出平移![]() )可视作图情况酌情给分)
)可视作图情况酌情给分)
10、解:(Ⅰ)依题意,![]() 由原点O到l的距离为
由原点O到l的距离为![]() ,得
,得
![]() 又
又![]()
![]() 故所求双曲线方程为
故所求双曲线方程为![]() …4分
…4分
(Ⅱ)显然直线m不与x轴垂直,设m方程为y=kx-1,则点M、N坐标(![]() )、(
)、(![]() )是方程组
)是方程组 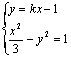 的解 消去y,得
的解 消去y,得![]() ①…6分
①…6分
依设,![]() 由根与系数关系,知
由根与系数关系,知![]()
![]() =
=![]() =
=![]() =
=![]() ……9分
……9分
![]() ∴
∴![]() =-23,k=±
=-23,k=±![]()
当k=±![]() 时,方程①有两个不等的实数根,故直线l方程为
时,方程①有两个不等的实数根,故直线l方程为![]() …12分
…12分
11、解![]() ,
,
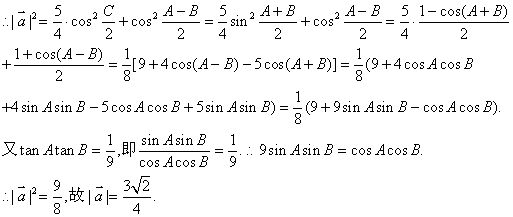
12、解(1)设点M的坐标为![]()
由![]() 由点Q在x轴的正半轴上,得
由点Q在x轴的正半轴上,得![]() .
.
所以,动点M的轨迹C是以(0,0)为顶点,以(2,0)为焦点的抛物线,除去原点.
(2)设直线![]()
![]()
设![]() 的两个实数根,由韦达定理得
的两个实数根,由韦达定理得
![]() ,
,
所以,线段AB的中点坐标为![]()
而![]()
![]() 轴上存在一点E,使△AEB为以点E为直角顶点的直角三角形,∴点F到x轴的距离不大于
轴上存在一点E,使△AEB为以点E为直角顶点的直角三角形,∴点F到x轴的距离不大于![]() 所以
所以 ![]()
化简得![]() ,解之得
,解之得![]() ,结合(*)得
,结合(*)得![]()
又因为直线![]() 的斜率
的斜率![]() 所以
所以![]() ,显然
,显然![]()
故所求直线![]() 的斜率k的取值范围为
的斜率k的取值范围为![]()
13、解:(1)设![]() =(x,y),则
=(x,y),则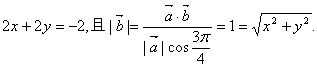
∴解得![]()
(2)![]() . ∴
. ∴![]()
∴![]()
=1+![]()
∴![]() ∴
∴![]()
14、![]() …3分
…3分
由![]() =0即
=0即![]()
即对称中心的横坐标为![]() …………6分(Ⅱ)由已知b2=ac
…………6分(Ⅱ)由已知b2=ac
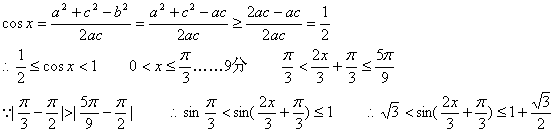 即
即![]() 的值域为
的值域为![]() 综上所述,
综上所述,![]()
![]() 值域为
值域为![]() …12分
…12分
15、解:(I)设A(0,y0)、Q(x0,0)、M(x,y),则![]()
又![]() ①……3分
①……3分
![]()
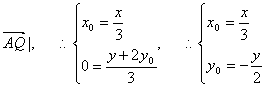 ②
②
将②代入①,有![]() …6分
…6分
(II)![]() 联立,
联立,
得![]()
![]() ③…8分,又
③…8分,又![]() …10分
…10分
而![]()
![]()
![]() ④………12分
④………12分
将③代入④整理有![]()
由题知![]() ………………………………14分
………………………………14分
16、解:(1)![]() ,…………2分
,…………2分
![]() ,
,
![]() .…4分,由
.…4分,由![]() 得
得![]() .
.
又![]() .…6分
.…6分
(2)由![]()
![]() ①…7分,又
①…7分,又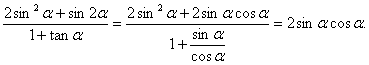 ……9分
……9分
由①式两分平方得
![]()
![]() …12分
…12分
18、解:(1)设![]() ,有
,有![]() ① …1分
① …1分
由![]() 夹角为
夹角为![]() ,有
,有![]() .∴
.∴![]() ②………3分
②………3分
由①②解得![]() ∴即
∴即![]() 或
或![]() …………4分
…………4分
(2)由![]() 垂直知
垂直知![]() …5分,由2B=A+C 知
…5分,由2B=A+C 知![]()
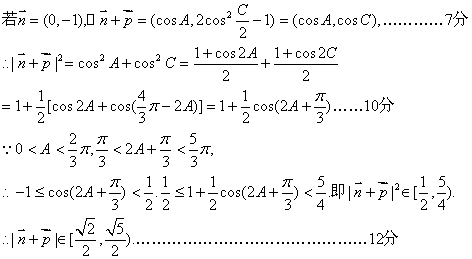
20、解:(1)由题意可得:点![]() 到两定点
到两定点![]() 的距离和为
的距离和为![]() ,故轨迹
,故轨迹![]() 是以
是以![]() 焦点的椭圆,其方程为
焦点的椭圆,其方程为![]() .
.
(2)显然![]() 与曲线
与曲线![]() 无交点,故直线
无交点,故直线![]() 的斜率存在,设
的斜率存在,设![]() 的方程为
的方程为![]() ,
,
![]() ,由
,由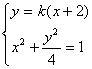 可得:
可得:![]() .
.
![]() ,且
,且![]() .
.
![]()
![]() ,
,![]() 四边形
四边形![]() 为平行四边形,若存在直线
为平行四边形,若存在直线![]() 使得四边形
使得四边形![]() 为矩
为矩
形,则![]() .
.![]() ,则有
,则有![]()
![]() ,代入可解得
,代入可解得![]() .设
.设![]() ,则
,则
![]() ,故不在直线
,故不在直线![]() 上,即不存在这样的直线
上,即不存在这样的直线![]() .
.