上学期联考高三数学试题
一、选择题：（每题5分，12小题共60分）
1、若
，则（ ）
A．
B.
C.
D.
2、在各项都为正数的等比数列
中，
，前3项和为21，则
( )
A.33 B.72 C.84 D.189
3、将函数
的图象沿向量
平移，则平移后的图象所对应
的函数解析式为（ ）
A.
B.
C.
D.
4、圆心在抛物线
上的动圆过点（0 ，
）且恒与定直线L相切，则
直线L的方程为（ ）
A.
B.
C.
D.
5、若非空集合
，则能使
成
立的所有
的集合是（ ）
A.
B. 
C. 
D.
6、在△
中，已知
，则
的值为（ ）
A.
B.2
C.
D.
7、若直线
和圆
，没有交点，则过（
）的直线与椭
圆
的交点个数（ ）
A.至多一个 B.2个 C.1个 D.0个
8、若
，则以下不等式中成立的是（ ）
A.
B. 
C. 
B.
9、如图在△中，
，
、
边上的高分别为
、
,则以
、
为焦点，且都过D、E的椭圆与双曲线的离心率的倒数和（ ）
|
|
|
A.
B.1
|
|
C.
D.2
10、
的图象（ ）
A.关于原点对称
B.关于
轴对称
C.关于直线
对称 D.无上述对称性
11、若点
处在由
三个不等式所确定的平面区域
内，则点
所在平面区域的面积为（ ）
A.1 B.2 C.4 D.8
12、某种电热器的水箱盛水是200升，加热到一定温度即可浴用，浴用时已
知每分钟放水34升，在放水的同时按10.9毫升/ 秒2的匀加速度作自动注水
（即t分钟自动注水2t2升），当水箱内的水量达到最小值时，放水自动停止，
现假定每人洗浴用水量为65升，则该热水器一次至多可供（ ）人洗浴。
A.3 B.4 C.5 D.6
二．填空题：（共16分）
13、已知函数
,若函数
图象关于原点对称，则
。
14、P为△内一点，且满足
，则△的面积与
△
的面积比为____________。
15、已知椭圆
，与双曲线
,具有相同的焦
点F1、F2设两曲线的一个交点为Q，∠QF1F2=90º,则双曲线的离心率为_______.
16、方程
的根称为
的不动点，若函数
有唯一不动
点，且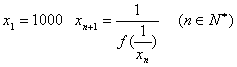
，则
.
上学期四校联考
| 座号 |
|
高三数学答题卷
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 |
|
|
|
|
|
|
|
|
|
一、选择题（每小题5分，共计60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题（每小题4分，共16分）
13、___________________________ 14、_________________________
15、___________________________ 16、_________________________
三、解答题（共74分，六大题）
17、（12分）已知函数
, 
,最小正周
期
. （1）求实数
的值。
（2）若
是△ABC的最小内角，求函数的值域。
18、（12分）已知集合
，判断
与
之间的关系并说明理由。
19、（12分）在△ABC中，角A、B、C所对的边分别是、
、
，
,
。（1）求
的值。
（2）若△ABC最长的边为1，求最短边的长。
20、设函数
的图象关于原点对
称，且
时，取得极小值
。
（1）
求
的值。
（2）
求证：当
时，
21、（12分）动椭圆C以坐标原点
为左焦点，以定直线
为左准线，点B是椭圆C的短轴的一个端点，线段BO的中点为M。
（1）求点M的轨迹方程。
（2）已知
, 
=(1，0) 
(0，1)，经过点（
，0）且以
为方向向量的直线
与点M的轨迹交于E、F两点，又点D
的坐标为（1，0）， 若∠EDF为钝角，求
的取值范围。
 |
22、（14分）已知函数
对任意实数
都有
。
（1）若t为自然数，试求的表达式。
（2）满足条件
的所有整数t能否成等差数列？若能构成等差数列，求出此数列，若不能构成等差数列，请说明理由。
（3）若t为自然数，且
时，
恒成立，求
的最大值。