| 姓名 | 班级 | 学号 | 时间 | ||||
| 课题 | 实数与向量的积 | 设计 | |||||
| 一、方法点拨: (1) 掌握实数与向量积的概念和运算法则,明确 (2) 理解两个向量共线的充要条件,并能利用它解决一些几何问题。 (3) 了解平面向量的基本定理,学会选取适当的基底表示其它向量。 二、知能达标: 1. 已知a、b不共线, (A)k+n=0 (B)k-n=0 (C)kn+1=o (D)kn-1=0 2.已知向量e1≠0,λ (A)λ=0 (B)e2=0 (C)e1 ∥e2 (D)e1 ∥e2 或λ=0 3.e1和 e2是表示平面内所有向量的一组基底,则下面四组向量中,不能作为一组基底的是( ) (A)e1和e1 +e2(B)e1-2 e2 与e2- 2 e1 (C)e1-2 e2与4e2- 2 e1 (D)e1 +e2与 e1 -e2 4. 已知
5.设a、b是两个不共线的向量, 三点共线,则k= 6.已知
| |||||||
| 8.设两个非零向量e1与e2不共线, ①如果 ②试确定实数k的值,使ke1+e2和e1+ke2共线。 9.在△OAB中,C是AB边上一点,且 10.已知a、b是不共线的向量, 且 |
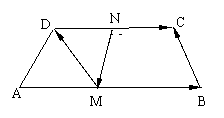 7.如图,已知梯形ABCD中,AB∥CD且AB=2CD,M, N分别是DC, AB中点,设
7.如图,已知梯形ABCD中,AB∥CD且AB=2CD,M, N分别是DC, AB中点,设