| 班级 | 姓名 | 学号 | 时间 | |||||||
| 课题 | 三垂线定理及其运用 | 设计 | ||||||||
| 一、方法点击 1、熟练掌握三垂线定理及其逆定理,善于在各种空间图形中找出符合三垂线定理或逆定理的面及该面的垂线。从而运用于证明两线垂直、计算点线距离、线面交角和面面交角等。 2、理解关系式cos 二、知能达标 1、如图:AB是圆的直径,C是圆周上一点,PC垂直圆所在平面,若BC=1,AC=2,则P到直线AB的距离为 ( D )
2.、PA、PB、PC是从P点引出的三条射线,它们每两条的夹角都是60° C 则直线PC与平面PAB所成的角是 ( C ) A B A 45° B60° C arccos
A、 4、在空间,下列命题正确的是 1,4 。 (注:把你认为正确的命题的序号都填上) C ① 如果两直线a、b分别与直线l都平行,那么a∥b。 ② 如果直线a与平面 ③ ④ 如果平面 5、如图,∠BAD=90°的等腰直角三角形ABD与正三角形CBD B D 所在的平面互相垂直,E是BC的中点,则AE与平面BCD所成的 E 角的大小 45° 。 C 6、如图,E,F分别为正方体的面ADD 1A1、面BCC 1B1中心,则四边形BFD 1E在该正方体的面上的射影可能是 2,3 。(要求:把可能的图的序号都填上)
A1 B1
E F
D C (1) (2) (3) (4)
7、如图,已知三棱锥A-BCD中,AB⊥CD,AC⊥BD,
D
B C | ||||||||||
| 8、已知AB是异面直线a、b的公垂线,AB=2cm,a、b成30°的角,在直线a上取一点P,使PA=4 cm,求P到直线b的距离。
B 9、已知斜三棱柱ABC-A1 B 1C1的各棱长均为2,侧棱与底面所成的角为
B1 A1 C
B A
|
 A . 1 B .2 C .
A . 1 B .2 C .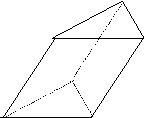 3、三棱柱ABC-A 1B 1C1,侧棱BB1在下底面上射影平行AC,如果侧棱BB1与底面所成的角为30°,∠B1 BC=60°,则∠ACB的余弦为 ( A ) C1
3、三棱柱ABC-A 1B 1C1,侧棱BB1在下底面上射影平行AC,如果侧棱BB1与底面所成的角为30°,∠B1 BC=60°,则∠ACB的余弦为 ( A ) C1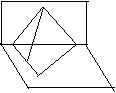 如果直线a与平面
如果直线a与平面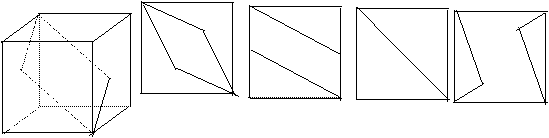 D1 C1
D1 C1 A B A
A B A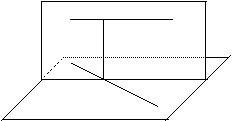 a A P
a A P 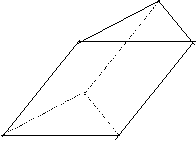 C1
C1