排列组合，二项式及概率
一）选择题
1. （2004.江苏）从4名男生和3名女生中选出4人参加某个座谈会，若这4人中必须既有男生又有女生，则不同的选法共有 ( D )
(A)140种 (B)120种 (C)35种 (D)34种
2. （2004.江苏）
的展开式中x3的系数是
( C )
(A)6 (B)12 (C)24 (D)48
3. （2004.江苏）将一颗质地均匀的骰子（它是一种各面上分别标有点数1，2，3，4，5，6的正方体玩具）先后抛掷3次，至少出现一次6点向上和概率是 ( D )
(A) (B) (C) (D)
4．(2004.全国理)
的展开式中常数项是 （ A ）
A．14 B．－14 C．42 D．－42
5．(2004.全国理)从数字1，2，3，4，5，中，随机抽取3个数字（允许重复）组成一个三位数，其各位数字之和等于9的概率为 （ D ）
A．
B．
C．
D．
6．（2004. 福建理）某校高二年级共有六个班级，现从外地转入4名学生，要安排到该年级的两个班级且每班安排2名，则不同的安排方案种数为 （ C ）
A．
B．
C．
D．
7．（2004. 福建理）若(1-2x)9展开式的第3项为288，则
的值是 （ A ）
A．2 B．1
C．
D．
8．（2004. 重庆理）某校高三年级举行一次演讲赛共有10位同学参赛，其中一班有3位，二班有2位，其它班有5位，若采用抽签的方式确定他们的演讲顺序，则一班有3位同学恰好被排在一起（指演讲序号相连），而二班的2位同学没有被排在一起的概率为： （ D ）
A．
B．
C．
D．
9．（2004. 辽宁卷）甲、乙两人独立地解同一问题，甲解决这个问题的概率是p1，乙解决这个问题的概率是 p2，那么恰好有1人解决这个问题的概率是B
A．
B．
C．
D．
10．（2004. 辽宁卷）有两排座位，前排11个座位，后排12个座位，现安排2人就座，规定前排中间的3个座位不能坐，并且这2人不左右相邻，那么不同排法的种数是B
A．234 B．346 C．350 D．363
11、（2004. 人教版理科）将4名教师分配到3所中学任教，每所中学至少1名，则不同的分配方案共有（ ）
A、12种 B、24种 C、36种 D、48种
二）填空题
12．（2004. 辽宁卷）口袋内装有10个相同的球，其中5个球标有数字0，5个球标有数字1，若从袋中摸出5个球，那么摸出的5个球所标数字之和小于2或大于3的概率是
.（以数值作答）
13．（2004.湖南理）若
的展开式中的常数项为84，则n=
9 .
14、(2004. 四川理）在由数字1、2、3、4、5组成的所有没有重复数字的5位数中，大于23145且小于43521的数共有（ C ）
A 56个 B 57个 C 58个 D 60个
15．（2004.湖北理）设随机变量
的概率分布为
4
.
16. (2004. 天津卷)若
，则
2004。(用数字作答)
(16) (2004. 天津卷)从
中任取2个数字，从
中任取2个数字，组成没有重复数字的四位数，其中能被5整除的四位数共有______________300个。(用数字作答)
17．（04. 上海春季高考）一次二期课改经验交流会打算交流试点学校的论文5篇和非试点学校的论文3篇。若任意排列交流次序，则最先和最后交流的论文都为试点学校的概率是__________
（结果用分数表示）.
18．（04. 上海春季高考）如图，在由二项式系数所构成的杨辉三角形中，第
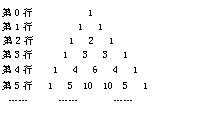___34 __行中从左至右第14与第15个数的比为
.
19. （2004. 重庆理）若在
的展开式中
的系数为
，则
.－2
20.（2004. 福建理）．某射手射击1次，击中目标的概率是0.9.他连续射击4次，且各次射击是否击中目标相互之间没有影响.有下列结论：
①他第3次击中目标的概率是0.9；
②他恰好击中目标3次的概率是0.93×0.1；
③他至少击中目标1次的概率是1-0.14.
其中正确结论的序号是 1，3 （写出所有正
确结论的序号）.
21、（2004.上海理）若在二项式(x+1)10的展开式中任取一项,则该项的系数为奇数的概率是 
. (结果用分数表示)
22．（2004.湖北理）将标号为1，2，…，10的10个球放入标号为1，2，…，10的10个盒子内，每个盒内放一个球，则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有 240
种.（以数字作答）
三）解答题
23．（2004.湖南理）（本小题满分12分）
甲、乙、丙三台机床各自独立地加工同一种零件，已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为
.
（Ⅰ）分别求甲、乙、丙三台机床各自加工零件是一等品的概率；
（Ⅱ）从甲、乙、丙加工的零件中各取一个检验，求至少有一个一等品的概率
23．解：（Ⅰ）设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件.
|
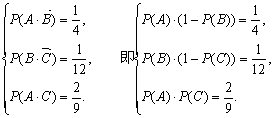
由①、③得
代入②得 27[P(C)]2－51P(C)+22=0.
解得
（舍去）.
将
分别代入
③、② 可得 
即甲、乙、丙三台机床各加工的零件是一等品的概率分别是
（Ⅱ）记D为从甲、乙、丙加工的零件中各取一个检验，至少有一个一等品的事件，
则
故从甲、乙、丙加工的零件中各取一个检验，至少有一个一等品的概率为
24．（2004. 福建理）（本小题满分12分）
甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中的6题，乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才算合格.
（Ⅰ）求甲答对试题数ξ的概率分布及数学期望；
（Ⅱ）求甲、乙两人至少有一人考试合格的概率.
24.本小题主要考查概率统计的基础知识，运用数学知识解决问题的能力.满分12分.
解：（Ⅰ）依题意，甲答对试题数ξ的概率分布如下：
| ξ | 0 | 1 | 2 | 3 |
| P |
|
|
|
|
甲答对试题数ξ的数学期望
Eξ=0×
+1×
+2×+3×
=
.
（Ⅱ）设甲、乙两人考试合格的事件分别为A、B，则
P(A)=
=
=
，
P(B)=
=
=
.
因为事件A、B相互独立，
方法一：
∴甲、乙两人考试均不合格的概率为
P(
)=P(
)P(
)=1－)(1－)=
.
∴甲、乙两人至少有一人考试合格的概率为
P=1－P()=1－=
.
答：甲、乙两人至少有一人考试合格的概率为.
方法二：
∴甲、乙两人至少有一个考试合格的概率为
P=P(A·)+P(·B)+P(A·B)=P(A)P()+P()P(B)+P(A)P(B)
=×
+
×+×=.
答：甲、乙两人至少有一人考试合格的概率为.
25．（2004.湖北理）（本小题满分12分）
某突发事件，在不采取任何预防措施的情况下发生的概率为0.3，一旦发生，将造成
400万元的损失. 现有甲、乙两种相互独立的预防措施可供采用. 单独采用甲、乙预防措施
所需的费用分别为45万元和30万元，采用相应预防措施后此突发事件不发生的概率为0.9
和0.85. 若预防方案允许甲、乙两种预防措施单独采用、联合采用或不采用，请确定预防
方案使总费用最少.
（总费用=采取预防措施的费用+发生突发事件损失的期望值.）
25．本小题考查概率的基本知识和数学期望概念及应用概率知识解决实际问题的能力，满分12分.
解：①不采取预防措施时，总费用即损失期望为400×0.3=120（万元）；
②若单独采取措施甲，则预防措施费用为45万元，发生突发事件的概率为
1－0.9=0.1，损失期望值为400×0.1=40（万元），所以总费用为45+40=85（万元）
③若单独采取预防措施乙，则预防措施费用为30万元，发生突发事件的概率为1－0.85=0.15，损失期望值为400×0.15=60（万元），所以总费用为30+60=90（万元）；
④若联合采取甲、乙两种预防措施，则预防措施费用为45+30=75（万元），发生突发事件的概率为（1－0.9）（1－0.85）=0.015，损失期望值为400×0.015=6（万元），所以总费用为75+6=81（万元）.
综合①、②、③、④，比较其总费用可知，应选择联合采取甲、乙两种预防措施，可使总费用最少.