平面向量
一）选择题
1．(2004.全国理)已知a、b均为单位向量，它们的夹角为60°，那么a+3b= （C ）
A．
B．
C．
D．4
2．（2004.湖北理）已知
为非零的平面向量. 甲：
（ B ）
A．甲是乙的充分条件但不是必要条件
B．甲是乙的必要条件但不是充分条件
C．甲是乙的充要条件
D．甲既不是乙的充分条件也不是乙的必要条件
3．（2004. 福建理）已知a、b是非零向量且满足(a－2b) ⊥a，(b－2a) ⊥b，则a与b的夹角是 （ B ）
A．
B．
C．
D．
4．（2004. 重庆理）若向量
的夹角为
，
,则向量
的模为 （ C
）
A．2 B．4 C．6 D．12
5、(2004. 四川理）已知平面上直线l的方向向量e=(-
)，点O(0,0)和点A(1,-2)在l上的射影分别为
和
，则
λe，其中λ=（ D ）
A 
B
-
C 2
D -2
6．（04. 上海春季高考）在
中，有命题
①
；②
；③若
，则为等
腰三角形；④若
，则为锐角三角形.
上述命题正确的是 （ C ）
（A）①② （B）①④ （C）②③ （D）②③④
7.(2004. 天津卷)若平面向量
与向量
的夹角是
，且
，则
(A)
(A)
(B) 
(C) 
(D) 
二）填空题
8.平面向量
中，已知
=(4，-3)，
=1，且
=5，则向量
______.
9．（2004.湖南理）已知向量a=
，向量b=
，则2a－b的最大值是
4
10、（2004.上海理）已知点A(1, －2),若向量
与={2,3}同向,
=2,则点B的坐标为 (5,4) ..
三）解答题
11．（2004.湖北理）（本小题满分12分）
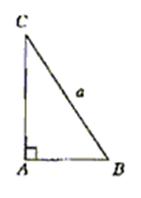
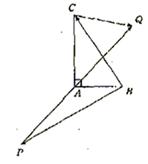
如图，在Rt△ABC中，已知BC=a，若长为2a的线段PQ以点A为中点，问
|
取何值时
的值最大？并求出这个最大值.
11．本小题主要考查向量的概念，平面向量的运算法则，考查运用向量及函数知识的能力，满分12分.
|
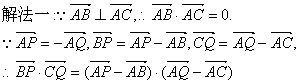
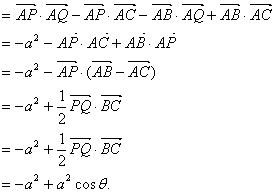
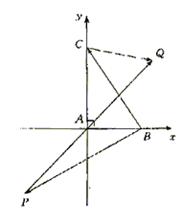
解法二：以直角顶点A为坐标原点，两直角边所在直线为坐标轴建立如图所示的平面直角坐标系.
|
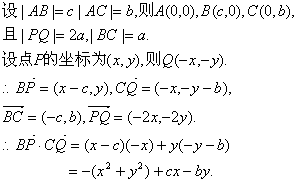
12. （04. 上海春季高考）（本题满分12分） 在直角坐标系
中，已知点
和点
，其中
. 若向量
与
垂直，求
的值.
12. 由
，得
，利用
，化简后得
，于是
或
，
，
.