平面向量测试题
班级 姓名 得分 .
一、选择题：
1、命题p：
=
，命题q：=，则p是q的……………………………………………………( )
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D) 非充分非必要条件
2、在平行四边形ABCD中，
=……………………………………………………( )
(A)
(B)
(C)
(D)
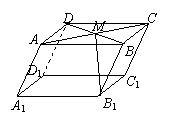3、如图，在平行六面体中，M是AC与BD交点，若
=，
=，
=
，则下列与
相等的是…………………………………（ ）
(A)－
＋＋ （B）＋＋
(C）－－＋ （D）－＋
4、设坐标原点为O，抛物线y2=2x与经过焦点的直线交于A、B，则
=…………………（ ）
(A)
（B）－ （C）3 （D）－3
5、如果
，
不共线，则下列四组向量共线的有…………………………………………………（
）
⑴2，－2；⑵－，－2＋2；⑶4－
，－
；⑷＋，2－2
(A)⑵⑶ (B) ⑵⑶⑷ (C) ⑴⑶⑷ (D)⑴⑵⑶⑷
6、、、是任意非零并且互相不共线，则在下列四个命题中：⑴(·)·－(·)·=0；⑵－<－；⑶(·)·－(·)·不与垂直；⑷(3＋2)·(3－2)=92－42,真命题有…………………………………………………………………………………………（
）
(A)⑴⑵ (B)⑵⑶ (C)⑶⑷ (D)⑵⑷
7、如果、、是任意向量，则下列等式不一定成立的是………………………………………（ ）
(A) (＋)＋=＋(＋)
(B) (＋)·=·＋·
(C) m(＋)=m＋m (D) (·)·=(·)
8、如果四边形ABCD是菱形，点P在对角线AC上（不含端点），则
=………………………（ ）
(A)
(＋
) , ∈(0,1) (B) (＋) , ∈(0,
)
(C)(－) , ∈(0,1) (D) (－) , ∈(0,)
9、如果A、B、C三点共线，并且A、B、C的纵坐标分别为2，5，10，则点A分的比为…（ ）
(A)
(B)
(C)－
(D) －
10、△ABC中，=，
=，·<0，S△ABC=
，=3，=5，则、夹角为（ ）
(A)30
(B) －150
(C)150
(D) 30或者150
11、△ABC中，若(a－c·cosB)sinB=(b－c·cosA)sinA，则这个三角形是……………………………（ ）
(A)底角不为45
的等腰△ (B) 锐角不为45的直角△
(C)等腰直角△ (D) 等腰或者直角△
12、△ABC中，“A=B”是“sinA=sinB”的………………………………………………（ ）条件
(A)充分不必要 (B) 必要不充分 (C)充要 (D) 非充分非必要
二、填空题：
13、非零向量=（2，－3q），=（3q，2q），则⊥的充要条件是
.
14、非零向量、满足＋= －，则、所成角为
.
15、如果向量、夹角120，并且=2，=5，则(2－)·=
.
16、抛物线
的焦点坐标为
.
三、解答题：
17、如果4－2=（－2，2
），=（1，），·=3，=4，求、夹角。
18、如果
，
分别是x、y方向的单位向量，
=2－4，
=－2＋，
=－－7
，
=－5－2，判断ABCD的形状。
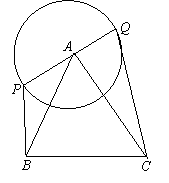19、△ABC中，BC=3
，AC=4，AB=2，PQ是以A为圆心，以为半径的圆的直径，求
的最大值与最小值，并且指出取得最值时
的方向。
20、已知平行六面体A—C1的底面ABCD是菱形，∠C1CB=∠C1CD=∠BCD=60。
⑴求证：C1C⊥BD；
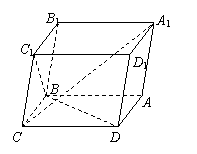⑵如果CD=2，C1C=
，求面C1BD与面CBD所成角的余弦；
⑶当
为多少时，可以得到A1C⊥平面C1BD，证明之！