| 班级 | 姓名 | 学号 | 时间 | |||||||
| 课题 | 平面与平面平行1 | 设计 | ||||||||
| 一、方法点击 1.掌握平面与平面平行的定义、判定定理和性质定理,并能运用这些知识进行论证和解题; 2.理解线线平行、线面平行和面面平行以及平行和垂直之间相互转化的辩证关系; 3.求线面距离、面面距离常转化为求点面距离。求点面距离有两种基本方法:(1)作图,找到能表示距离的线段计算之;(2)体积法。 4.能根据定义、定理的条件和结论进行思考,是寻求解题方法的有效途径。 二、知能达标 1.下列命题正确的是 ( B ) ①平行于同一条直线的两个平面平行 ②垂直于同一条直线的两个平面平行 ③平行于同一个平面的两个平面平行 ④垂直于同一个平面的两个平面平行 A. ①④ B. ②③ C. ①③ D. ②④ 2.平面 A.平行 B.相交 C.平行或相交 D.以上都不对 3.已知直线a∥平面 A.垂直 B.相交但不垂直 C.平行 D.重合 4.设平面 A. d1= d2 B. d1 <d2 C. d1 ≤d2 D. d1 ≥d2 5.两个平面间的三条线段,它们平行且相等,则两平面的为置关系为 平行或相交 。 6.已知 则CS= 16或272 . 7.如果平面 8.如图,直线AB、CD是异面直线,且于三平面分别相交于点A、E、及C、F、, AD∩
B
| ||||||||||
| 9.正方体ABCD -A1B1 C1 D1中, M、N分别为A1B1 、A1D1中点, E、F分别为B1C1、 C1D1中点.求证:(1) E、F、B、D四点共面;(2)平面AMN∥平面EFDB.
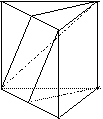
10.如图,直三棱柱ABC-A1B1C1中,B1C1=A1C1,AC1⊥A1B,M、N分别是A1B1、AB的中点.(1)求证:C1 M⊥平面A1AB B1;(2)求证:A1B⊥A M;(3)求证:平面AMC1∥平面NB1C;(4)求A1B与B1C所成的角。
M B1 A C N B | ||||||||||
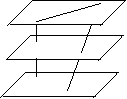 求证:EFGH是平行四边形。 C
求证:EFGH是平行四边形。 C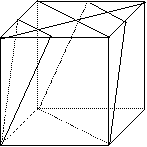
 A1 C1
A1 C1