 高三模拟考试数学卷(保密卷)
高三模拟考试数学卷(保密卷)
数 学 试 卷
(满分150分,答卷时间120分钟)
第Ⅰ卷(满分60)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设命题![]() 或
或![]() ,命题
,命题![]() 或
或![]() ,那么
,那么
A .若![]() 成立则
成立则![]() 成立
B.若
成立
B.若![]() 成立则
成立则![]() 成立
成立
C .若![]() 成立则
成立则![]() 成立
D.若
成立
D.若![]() 成立则p成立
成立则p成立
2.设曲线y=x2+x-1在点M处切线斜率为-1,则点M的坐标为
A.(0, -1) B.(-1,-1)
C.(-1,0) D.(1,1)
3.数列{an}的前n项和为Sn,且log3Sn=n,则{an}
A.是公比为3的等比数列 B.是公比为![]() 的等比数列
的等比数列
C.是公差为3的等差数列 D.既不是等差数列也不是等比数列
4.一个总体共有10个个体,用简单随机抽样的方法从中抽出一容量为3的样本,则某特定个体入样的概率是
A.![]() B.
B. ![]()
C.![]() D.
D.![]()
5.对甲、乙两种种子进行发芽试验,共试验6次,每次甲、乙两种种子各选10粒,发芽数如下:
| 甲 | 6 | 5 | 8 | 4 | 9 | 6 |
| 乙 | 8 | 7 | 6 | 5 | 8 | 4 |
根据以上数据,对两种种子平均发芽数和波动性作如下判断
A.甲平均发芽数多、波动小 B.乙平均发芽数多、波动小
C.甲、乙平均发芽数一样多,甲波动小 D.甲、乙平均发芽数一样多,乙波动小
6.函数![]() 的图象是
的图象是
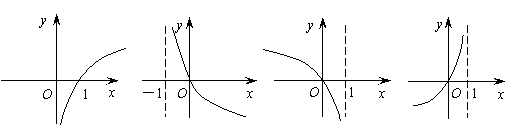 A B
C
D
A B
C
D
7.函数![]() ,
,![]() 的值域是
的值域是
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8.将函数![]() 的图象按向量a平移后,得到的函数解析式为
的图象按向量a平移后,得到的函数解析式为![]() ,则向量a为
,则向量a为
A.(1,1) B.(1,-1) C.(-1,1) D.(-1,-1)
9.把函数y=cosx的图象上的所有点的横坐标缩小到原来的一半,纵坐标扩大到原来的两倍,然后把图象向左平移![]() 个单位,则所得图象表示的函数的解析式为
个单位,则所得图象表示的函数的解析式为
A.y=2sin2x B.y=-2sin2x
C.y=2cos(x+![]() )
D.y=2cos(
)
D.y=2cos(![]() )
)
10.已知定义域为自然数集N的函数f (x)满足f (x+1)= f (x)+2x,且f (0)=0,则f (2003)=
A.2002![]() 2001
B.2003
2001
B.2003![]() 2002
2002
C.20032
D.2003![]() 2004
2004
11.下列判断,正确的是
A.![]() 是函数f (x)为奇函数的充要条件
是函数f (x)为奇函数的充要条件
B.![]() 是函数f (x)为奇函数的必要非充分条件
是函数f (x)为奇函数的必要非充分条件
C.设![]() 为正常数
为正常数![]() 为奇函数的充要条件
为奇函数的充要条件
D.设![]() 为正常数),
为正常数), ![]() 为奇函数的充要条件
为奇函数的充要条件
12.已知定义域为R的函数f (x)的值域为R+,函数g (x)的图象与函数f (x)的图象关于直线y=x对称,则函数y=g(4-x2)的单调增区间为
A.(-∞,0] B.(-2,0] C.[0,2) D.[0,+∞)
高三模拟考试(三)
数 学 试 卷
第Ⅱ卷(满分90分)
| 题 号 | 二 | 17 | 18 | 19 | 20 | 21 | 22 | 总 分 | 结分人 | 核分人 | ||||||
|
|
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.已知等差数列![]() 的前
的前![]() 项和为Sn,且
项和为Sn,且![]() ,则S13=_________.
,则S13=_________.
14.某质点作直线运动的路程S(cm)与时间t(s)的函数关系是S=2t2—3t+1,则质点在t=2时的瞬时速度为 (cm/s).
15.已知![]() ,
,![]() ,则
,则![]() 的值是
.
的值是
.
16. 已知ΔABC中,A(0,1),B(2,4),C(6,1),P为平面上任一点,点M、N分别使![]() ,
,![]() .给出下列关于命题:①
.给出下列关于命题:① ![]() ; ②直线MN的方程是3x+10y-28=0;③直线MN必过ΔABC的外心; ④向量
; ②直线MN的方程是3x+10y-28=0;③直线MN必过ΔABC的外心; ④向量![]() (
(![]() R+)所在射线必过点N.其中真命题序号是 (要求将所有真命题的序号都填上).
R+)所在射线必过点N.其中真命题序号是 (要求将所有真命题的序号都填上).
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
|
17.(本小题满分12分)
已知向量a=(4,2),b=(6,y),且a⊥b.
(Ⅰ)求y;
(Ⅱ)求a+b与a的夹角.
|
已知函数![]() 在
在![]() 处有极值,曲线
处有极值,曲线![]() 处的切线平行于直线
处的切线平行于直线![]() 求函数
求函数![]() 的极大值与极小值的差.
的极大值与极小值的差.
|
19.(本小题满分12分)
在![]() 中,记三个内角A,B,C所对的边分别为a,b,c,外接圆半径为R。
中,记三个内角A,B,C所对的边分别为a,b,c,外接圆半径为R。
给出条件:①c=![]() ;②R=
;②R=![]() ;③C=75º;④
;③C=75º;④![]() 。
。
在上述条件中选取三个条件确定ΔABC,并求相应ΔABC的面积。
答:所选条件_________________________________________。
解:
|
20.(本小题满分12分)
已知公差大于零的等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足a1a6=21,
,且满足a1a6=21, ![]() .
.
(Ⅰ)求数列![]() 的通项
的通项![]() ;
;
(Ⅱ)若数列![]() 使bn=
使bn=![]() ,求数列
,求数列![]() 前n项之和
前n项之和![]() ;
;
(Ⅲ)若数列![]() 是等差数列,且
是等差数列,且![]() ,求非零常数p.
,求非零常数p.
|
21.(本小题满分12分)
某种夏季服装,在春夏之交价格呈上升趋势,某商场第一周销售该服装时定价为100元/件,并且以后每周涨价10元/件,当价格涨到150元/件时,将保持价格不变平稳销售一段时间,第10周开始考虑到夏季即将过去,故每周减价10元/件,直到第16周末,该服装不再销售.
(Ⅰ)试建立销售价格p与周次t的函数关系;
(Ⅱ)若此服装每件进价Q与周次t之间的关系Q=-0.625(t-8)2+110,t∈[0,16],
t∈N.试问该服装第几周每件销售利润L最大?
|
22.(本小题满分14分)
已知向量p![]() q
q![]() ,m
,m![]() ,且(p- q)∥ m,y与x的函数关系式为y=f(x).
,且(p- q)∥ m,y与x的函数关系式为y=f(x).
(I)求=f(x);
(II)判断并证明函数y=f(x)当x>a时的单调性;
(III)我们利用函数y=f(x)构造一个数列{xn},方法如下:对于f(x)定义域中的x1,令 x2=f(x1) ,x3=f(x2),…, xn=f(xn-1) ,….在上述构造数列的过程中,如果x![]() …)在定义域中,构造数列的过程将继续下去;如果xi不在定义域中,则构造数列的过程停止.如果取f(x)定义域中任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求实数a的值.
…)在定义域中,构造数列的过程将继续下去;如果xi不在定义域中,则构造数列的过程停止.如果取f(x)定义域中任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求实数a的值.
 高三模拟考试(三)
高三模拟考试(三)
数学试卷参考答案和评分标准
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.A 2.B 3.D 4.A 5.D 6.C 7.D 8.B 9.B
10.B 11.C 12.B
二、填空题:本大题共4小题,每题4分,共16分.把答案填在题中横线上.
13.13 14.5
15.![]() 16. ②、 ④
16. ②、 ④
三、解答题:本大题共6小题,共74分..解答应写出文字的说明、证明过程或演算步骤.
17.(1)由a⊥b,得 4![]() 6+2y=0. ……………………………………………4分
6+2y=0. ……………………………………………4分
![]() y=-12.
……………………………………………5分
y=-12.
……………………………………………5分
(2)由a=(4,2) , b=(6,-12), 得a+b=(10,-10).
a
=![]() ,a+b=
,a+b=![]() , ………………………………………………7分
, ………………………………………………7分
cosθ=![]() .
………………………………10分
.
………………………………10分
∵θ∈[0,![]() ], ∴θ=arccos
], ∴θ=arccos![]() .
………………………………………12分
.
………………………………………12分
18.解:![]() 由于f(x)在x=2处有极值,
由于f(x)在x=2处有极值,
![]() ①.
…… …………………………………2分
①.
…… …………………………………2分
又![]() 处的切线平行于
处的切线平行于![]() ②,4分
②,4分
解①、②,得![]() …………………………6分
…………………………6分
令![]() ,得x1=0,x2=2. ………………………………………8分
,得x1=0,x2=2. ………………………………………8分
由于在x=0附近,![]() 左正,右负,而在x=2附近,
左正,右负,而在x=2附近,![]() 左负,右正,
左负,右正,
所以![]() 是函数的极大值,
是函数的极大值,![]() 是函数的极小值.………………………………10分
是函数的极小值.………………………………10分
于是![]()
故函数的极大值与极小值的差为4.……………………………………………12分
19.解法一:①、②、④ ………………………………………………………………4分
![]() c=
c=![]() ,R=
,R=![]() , 由正弦定理,得
, 由正弦定理,得
sinC=![]() ,
,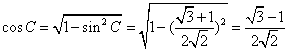 .…7分
.…7分
由![]() 及余弦定理,
及余弦定理,
得![]() )
)
![]() a=2,b=
a=2,b=![]() .…………………………………………………………10分
.…………………………………………………………10分
![]() ΔABC的面积S=
ΔABC的面积S=![]() absinC=
absinC=![]()
![]() 2
2![]()
![]()
![]()
![]() =
=![]() .…………12分
.…………12分
解法二:①、③、④.…………………………………………………………4分
![]() c=
c=![]() ,C=75º,
,C=75º,![]() .
.
cos75º= cos45ºcos30º- sin45ºsin30º= ![]() .…………………………6分
.…………………………6分
in75º= sin45ºcos30º+ cos45ºsin30º=![]() . …………………………7分
. …………………………7分
由余弦定理,得![]()
![]() a=2,b=
a=2,b=![]() . ……………………………………………………………10分
. ……………………………………………………………10分
![]() ΔABC的面积S=
ΔABC的面积S=![]() absinC=
absinC=![]()
![]() 2
2![]()
![]()
![]()
![]() =
=![]() . …12分
. …12分
解法三:②、③、④. …………………………………………………………4分
![]() R=
R=![]() ,C=75º,
,C=75º,
∴ 由正弦定理,得 c=2RsinC=2![]() sin75º=2
sin75º=2![]()
![]() =
=![]() .
.
cos75º= cos45ºcos30º- sin45ºsin30º= ![]() ,……………………7分
,……………………7分
由![]() 及余弦定理,得
及余弦定理,得![]()
![]() a=2,b=
a=2,b=![]() .………………………………………………………………10分
.………………………………………………………………10分
![]() ΔABC的面积S=
ΔABC的面积S=![]() absinC=
absinC=![]()
![]() 2
2![]()
![]()
![]()
![]() =
=![]() . ……12分
. ……12分
20.解:(Ⅰ)![]() 为等差数列,
为等差数列,![]() ,∴
,∴![]()
又![]() ,
,![]() 是方程
是方程![]() 的两实根.
的两实根.
又公差![]()
![]() …………………………………………2分
…………………………………………2分
∴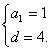
![]() ……………………………………………………4分
……………………………………………………4分
(Ⅱ)由(Ⅰ),得![]() .
.
∴![]() =
=![]() .
.
当x=![]() 1时,
1时,![]() =n; ……………………………………………………6分
=n; ……………………………………………………6分
当x![]()
![]() 1时,
1时,![]() =
=![]() .………………………………8分
.………………………………8分
(Ⅲ)由(Ⅰ)知
![]() .…………………10分
.…………………10分
![]()
![]() 是等差数列,
是等差数列, ![]() ,
,
即![]() .………………………12分
.………………………12分
21.解:(Ⅰ)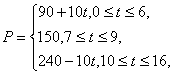 其中t∈N. …………………6分
其中t∈N. …………………6分
(Ⅱ)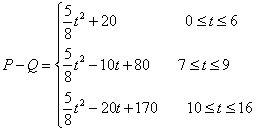 (其中t∈N) ……………… 10分
(其中t∈N) ……………… 10分
t=6时,Lmax=42.5,即第6周销售利润最大.……………………………12分
22.解:(Ⅰ)∵向量![]() ,
,![]() ,
,
∴![]() . ………………………………………………………2分
. ………………………………………………………2分
由(![]() ,得(a-x)
,得(a-x)![]() y-(x+1-a)
y-(x+1-a)![]() 1=0.
1=0.
由x![]() a,得y=
a,得y=![]() ,即f(x)=
,即f(x)= ![]() .……………………………… 4分
.……………………………… 4分
(Ⅱ)对任意的x1,x2,使a< x1<x2,
∵f(x2)- f(x1)= ![]() -
-![]() = –1+
= –1+![]() ―(–1+
―(–1+![]() )
)
=![]() ……………………………………………………………………6分
……………………………………………………………………6分
∵a< x1<x2,∴x2-x1>0,a-x2<0,,a-x1<0,∴f(x2)- f(x1)>0. …………8分
函数y=f(x)当x>a时的单调递增. …………………………………………… 9分
(III)根据题意,应满足![]() 时,
时,![]() 无解,
无解,
即![]() 时,(1+a)x=a2+a-1无解.……………………………………………11分
时,(1+a)x=a2+a-1无解.……………………………………………11分
由于x=a不是方程(1+a)x=a2+a-1的解,
所以,对于任意x∈R,方程(1+a)x=a2+a-1无解.
所以a=-1. …………………………………………………………………14分