高三年级第三次阶段测试试题数学卷

高三年级第三次阶段测试试题数学卷

数学试卷

第I卷（选择题 共60分）

一、选择题：（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．若非空集合P与Q的关系P Q，则下列结论中正确的是　　　　　　　　　　　　　　　　（　　）

　　　 A．P∩Q=P　　　　　　　B．P∩Q=　　　　　　 C．QP　　　　　　　　 D．P∩Q≠

2．若是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．第二象限角　　　　　　　　　　　　　　　　　　　　B．第一或第三象限角　　　　　　　　　　　

　　　 C．第三象限角　　　　　　　　　　　　　　　　　　　　D．第二或第三象限角

3．数的单调递减区间是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　 B．

　　　 C．　　　　　　　　D．

4．不等式的解集是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（ 　 ）

　　　 A．　　　　　　　　　　　　　　　　　　　　 B．{xx≥1}

　　　 C．{xx≥1且x=－2}　　　　　　　　　　　　　　　 D．{xx≥1或x=－2}

5．将抛物的图象按向量平移，使其顶点与坐标原点重合，则=（　　）

　　　 A．（2，－3）　　　　　B．（－2，－3）　　　 C．（－2，3）　　　　　D．（2，3）

6．等比数列{a_n}记S_n=a₁+a₂+…+a_n，如果则S₆=　　　　　　　 （　　）

　　　 A．18　　　　　　　　　　　B．144　　　　　　　　　　 C．14　　　　　　　　　　　D．－102

7．是定义在R上的奇函数，它的最小正周期为T，则的值为　　　　　　（　　）

　　　 A．　　　　　　　　　　　B．0　　　　　　　　　　　　C．T　　　　　　　　　　　　D．－

8．设则集合中元素个数是　　　　　　　　　 　　（　　）

　　　 A．2　　　　　　　　　　　　B．4　　　　　　　　　　　　C．3　　　　　　　　　　　　D．无穷多个

9．过点（－4，0）作直线l与圆x²+y²+2x－4y－20=0交于A、B两点，如果AB=8，则（　　）

　　　 A．l的方程为5x+12y+20=0或x+4=0

　　　 B．l的方程为5x－12y+20=0或x+4=0

　　　 C．l的方程为5x－12y+20=0

　　　 D．l的方程为5x+12y+20=0

10．某爱国教育基地在星期一到星期五要接待三所学校的师生来参观，每天只能安排一所学校。如果甲学校要连续参观两天，而其余学校都参观一天，则不则的安排方法种数共有

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．36　　　　　　　　　　　B．24　　　　　　　　　　　 C．60　　　　　　　　　　　D．120

11．6支签字笔与3本笔记本的金额之和大于24元，而4支签字笔与5本笔记本的金额之和小于22元，则2支签字笔与3本笔记本的金额比较结果是　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．3本笔记本贵　　　B．2支签字笔贵　　　C．相同　　　　　　　　　 D．不确定

12．a、b是任意实数，记a+b、a－b、b－1中的最大值为M，则　　　　　　　　　　　　（　　）

　　　 A．M≥0　　　　　　　　　B．0≤M≤　　　　　C．M≥1　　　　　　　　　D．M≥

第Ⅱ卷（非选择题 共90分）

二、填空题：本大题共4小题，每小题4分，共16分；把答案填在题中的横线上.

13．若　　　　　　　　　  

14．已知直线l过点A（3，－1），且与向量垂直，则直线l的一般方程　　　　　　

15．已知函数y=f(x)是偶函数，y=g(x)是奇函数，

它们的定义域是[－π，π]，且它们在

上的图象如图所示，则不等式

的解集是　　　　　　　　　  

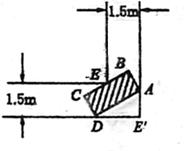
16．如图，一条直角走廊宽为1.5m，一转动

灵活的平板手推车，其平板面为矩形，宽

为1m.问：要想顺利通过直角走廊，平板

手推车的长度不能超过　　　　　　　   米.

三、解答题（第17至21题每题12分、第22题14分，共74分）

17．甲、乙两名射手在一次射击中的得分为两个相互独立的随机变量ξ与η，且ξ、η的分布列为：

η 1 2 3 p 0.3 b 0.3

ξ 1 2 3 p a 0.1 0.6

　 （1）求a、b的值；

　 （2）甲、乙两名射手在一次射击中的得分均小于3的概率谁更大？

　 （3）计算ξ、η的期望与方差，并以此分析甲乙的技术状况.

18．平面直角坐标系有点

　 （1）求向量的夹角θ的余弦用x表示的函数f(x);

　 （2）求θ的最值.

19．设数列{a_n}前n的项和为 S_n，且其中m为常数，

　 （1）求证{a_n}是等比数列

　 （2）若数列{a_n}的公比满足q=f(m)且，为等差数列，并求

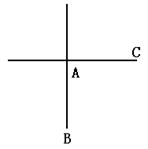
20．如图，两铁路线垂直相交于站A，若已知AB=100公里，甲火车从A站出发，沿AC方向以50公里/小时的速度行驶，同时乙火车以v公里/小时的速度从B站沿BA方向行驶至A站即停止前行（甲车仍继续行驶）.

　 （1）用v表示甲、乙两车的最近距离（两车的车长忽略不计）；

　 （2）若甲、乙两车开始行驶到甲、乙两车相距最近时，所用时间为t₀小时，问v为何值时，t₀最大.

21．已知函数f(x)是定义在R上的偶函数，当

　 （1）求当x<0时，f(x)的解析式；

　 （2）试确定函数y=（x≥0）的单调区间，并证明你的结论；

　 （3）若证明：

22．函数的定义域为R，且

　 （1）求证：a>0,b<0；

　 （2）若上的最小值为，试求f(x)的解析式；

　 （3）在（2）的条件下记试比较

　　　　的大小并证明你的结论.

高三年级第三次阶段测试试题

数学试卷参考答案

一、ACCDA　 CBCAB　BD

二、13．　 14．　 15．　16．

三、17．解：（1）∵a+0.1=0.6=1 , ∴a=0.3, 同理b=0.4;

　 （2）p(ξ<3)=0.3+0.1=0.4;　p(η<3)=0.3+0.4=0.7　∴p(ξ<3)< p(η<3)

　 （3）Eξ=1×0.3+2×0.1+3×0.6=2.3

　　　　Eη=1×0.3+2×0.4+3×0.3=2

　　　　Dξ=(x₁－Eξ)²p₁+(x₂－Eξ)²p₂+(x₃－Eξ)²p₃

　　　　　 =(1－2.3)²·0.3+(2－2.3)²·0.1+(3－2.3)²·0.6=0.81

同理Dη=(1－2)²·0.3+(2－2)²·0.4+(3－2)²·0.3=0.6

由计算结果Eξ> Eη，说明在一次射击中，甲的平均得分比乙高，但Dξ>Dη说明甲得分的稳定性比乙差，因而，甲乙两人的技术都不够全面.

18．解：（1）

　　　　

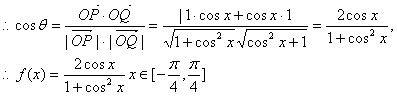
　 （2）

　　　　

19．解（1）由两式相减得

是等比数列（6分）

　

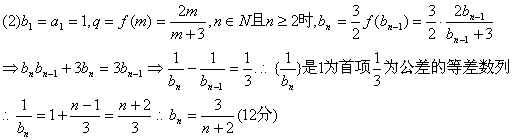
20．解：（1）设乙车行驶t小时到D，甲车行驶t小时到E，1°若0≤tV≤100，

则DE²=AE²+AD²=(100－tV)²+(50t)²=(2500+V²)t²－200Vt+10000

当t=时，DE²取最小值，DE也取最小值，其最小值为

2°若tV>100时，乙车停止，甲车继续前行DE越来越大，无最大值.

由1°、2°知，甲、乙两车的最近距离为公里（6分）

（2）t­₀==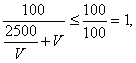当且仅当V=

即V=50公里/小时时，t₀最大.（12分）

答：v=50/小时时，t₀最大.

21．解：（1）若x<0，则－x>0，∵f(x)是偶函数，

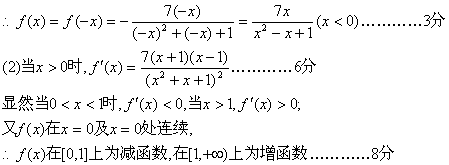
　 （3）

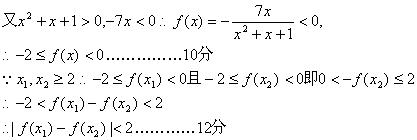
22．解（1）∵f(x)定义域为R，

　（2）由（1）知f(x)在[0，1]上为增函数，

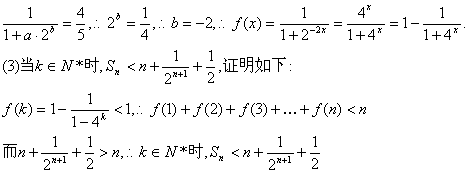
囿有篇幅，每题只给出一种解法，若有其它作法，请酌情相应给分