高中数学联合竞赛模拟试题三

高中数学联合竞赛模拟试题三

第一试

一、选择题（每小题6分，共计36分）

1.定义在(－∞，－2)∪(2，＋∞)上的函数f(x)＝的奇偶性为
A.是奇函数不是偶函数　　　　　　　　　　B.是偶函数不是奇函数
C.既是奇函数又是偶函数　　　　　　　　　D.既不是奇函数又不是偶函数

2.把直线l沿y轴平移sinθ－cosθ(≠0)个单位，再沿x轴平移(＞0)个单位，所得直线与原直线重合，则原直线的斜率为
A.不存在　　　　　　B.　 C.　 D.

3.从正方体的8个顶点中取出3个，使至少有两个顶点在同一条棱上，其取法数为
A.44　　　　　　　　B.48　　　　　　　　C.50　　　　　　　　D.52

4.对于函数f(x)＝，记f₂(x)＝f(f(x))，f₃＝f(f₂(x))，……，f_n(x)＝f(f_n－1(x))，又记M为f₁₉₉₈(x)＝x实根的解集，则M为
A.Φ　　　　　　　　 B.R　　　　　　　　 C.单元素集合　　　　D.二元素集合

5.设递增正数列a₁，a₂，…，a_n是分母为60的最简真分数，则π＝
A.0　　　　　　　　 B.8　　　　　　　　 C.16　　　　　　　　D.30

6.存在x₁，x₂，…，x_n满足x＋1＝0，且使＝0成立的充要条件是
A.2n　　　　　　　 B.4n　　　　　　　 C.6n　　　　　　　 D.8n

二、填空题(每小题9分，共计54分)

1.给定递推数列，若T＝1998是使得x_T＋1＝x_T＋2＝1的最小正整数，则＝___________.

2.在平面α上有一个△ABC，∠ABC＝105°，AC＝2()，在平面α的两侧各有一点S和T，满足SA＝SB＝SC＝，TA＝TB＝TC＝5，则ST＝___________.

3.过双曲线x²－＝1的右焦点作直线L交双曲线于A、B两点，若实数λ使得AB＝λ的直线L恰有3条，则λ＝_____________.

4.已知函数f(x)、g(x)在R上有定义，且f(x－y)＝f(x)g(y)－g(x)f(y)，若f⑴＝f⑵≠0，则g⑴＋g(－1)＝___________________.

5.正实数x，y，z满足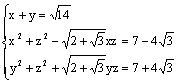，则z＝_____________.

6.一副桥牌有52张牌，将其排成一横行，任意两张A都不相邻的排列数为____________.

三、(20分)将一个10×16的矩形铁皮，从四个角上各建取一个边长为x的正方形(0＜x＜5)，然后做成一个无盖的长方体容器.
⑴写出容器的容积y与x的函数关系式；
⑵求y的最大值，并求相应的x的值.

四、(20分)对于α、β∈[0，2π)，记x＝sinα＋sinβ，y＝cosα＋cosβ，求直角坐标系上点(x，y)的轨迹.

五、(20分)求证：对于任给的正数a，必存在一个自然数N，使每一个大于N的自然数n都有惟一的自然数f(n)，满足.

第二试

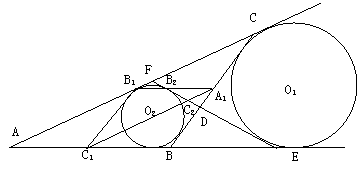一、（50分）作两个不等圆⊙O₁，⊙Q₂的四条公切线，如图，点A为两外公切线的交点，点D为两内公切线的交点，点B，C，E，F是两类公切线的交点，记A₁，B₁，C₁分别为BC，CA，AB的中点，若EF与A₁B₁交于B₂，与A₁C₁交于C₂，求证：B₁，C₁，C₂，B₂共圆.

二、（50分）设有两组正数：0＜x₁≤x₂≤x₃≤……≤x_n＜1，0＜y₁≤y₂≤y₃≤……≤y_n，
求证：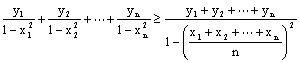

三、（50分）设S_n＝{1，2，……，n}(n≥5)，取XS_n，YS_n(X，Y无顺序)，若XY或YX，则称X，Y为一对“包含子集对”，否则称为“非包含子集对”，问S_n中是“包含子集对”多还是“非包含子集对”多？证明你的结论。