高中数学联合竞赛模拟试题四
第一试
一、选择题（每小题6分，共计36分）
1.满足(an－1)(an＋1＋1)＝0(n＝1，2，3，……，99)的数列共有
A.1个 B.3个 C.2100个 D.无穷多个
2.已知函数f(x)＝x2－2ax＋2a＋4的定义域为R，值域为[1，＋∞)，则a的取值为
A.区间[－1，3] B.区间(－∞，－1)∪(3，＋∞)
C.当x＞－
时，a≤
；当x＜－时，a≥ D.集合{－1，3}
3.
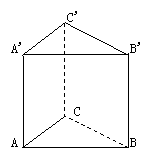如图，五面体ABC－A'B'C'中，AB＝A'B'，则AA'，BB'，CC'共点的充要条件是
A.BC∥B'C'且AC∥A'C' B.BC≠B'C'且AC≠A'C'
C.AA'≠BB'，且∠BAA'≠∠B'A'A D.面ABC与面A'B'C'不平行
4.不同的四点A(x1，y1)，B(x2，y2)，C(x3，y3)，D(x4，y4)在抛物线y＝ax2＋bx＋c(a≠0)上，且满足x1＋x4＝x2＋x3，则AD与BC的关系适合
A.AD∥BC B.AD⊥BC
C.AD与BC相交但不垂直
D.不能确定，与四个点的坐标具体取值有关
5.已知(1＋xi)4n＋2(x∈R，i2＝－1)展开式中的实部是关于x的多项式，则此多项式的系数和为
A.(－1)n22n＋1 B.0 C.22n＋1 D.－22n＋1
6.在双曲线xy＝k(k≠0)的一支上任取三点A，B，C，则△ABC的形状为
A.锐角三角形 B.钝角三角形 C.直角三角形 D.不能确定
二、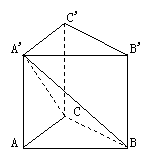
填空题(每小题9分，共计54分)
＝___________.
1.不等式
的解集为___________.
2.如图，直三棱柱ABC－A'B'C'中，底面是等腰直角三角形，∠ACB＝90°，AC＝1，AA'＝
，连结A'B，A'C，则侧面A'BC与面A'AB所成角的正切值为___________.
3.设f(x)在R上为增函数，若方程x＋f(x)＝m的解为p，则方程x＋f－1(x)＝m的解是___________.
4.已知1＋
(m，n是正整数)，则n≡___________(mod1999).
5.有5个匣子，每个匣子有一把钥匙，并且钥匙不能通用，如果随意在每一个匣子内放入一把钥匙，然后把匣子全部锁上，要求砸开一个匣子后，能相继用钥匙打开其余4个匣子，那么钥匙的放法有___________种.
三、(20分)若四面体相对棱中点的3条连线都相等，则这个四面体的对棱两两垂直。
四、(20分)已知直线l:y＝kx＋h(kh≠0)与x轴交于A点，与y轴交于B点，且与椭圆
＝1(a＞b＞0)没有公共点，求证：AB＞a＋b
五、(20分)已知a0，a1，a2，……，an为等差数列，f(x)＝
(b＞0)
求证：
[f(x)]k[f(1－x)]n－k＝a0f(1－x)＋anf(x)
第二试
一、（50分）梯形ABCD中，CD∥AB，∠ABC与∠BAD均为锐角，连结对角线AC，BD，求证：必可把△ABC分成四个互不重叠的三角形X1，X2，X3，X4，把△ABD也分成四个互不重叠的三角形Y1，Y2，Y3，Y4，使得Xi≌Yi(i＝1，2，3，4)
二、（50分）对于公差为d≠0的等差数列{an}，求证：数列中不同两项之和仍是这个数列中一项的充要条件是：存在m≥－1，使a1＝md.
三、（50分）将直线上a＋b＋c个点中的a个点染成红色，b个点染成黄色，c个点染成蓝色，并使同色点互不相邻，其染色方法的种数记为F(a，b，c).显然有
F(1，1，1)＝6，F(a，b，a＋b＋2)＝0，
0 当a－b＞1时
0 当a＞1时
F(a，b，0)＝ 1 当a－b＝1时 F(a，0，0)＝
2 当a－b＝0时
1 当a＝1时
⑴证明：对不全为1的正整数a，b，c，有递推式
F(a，b，c)＝F(a－1，b－1，c)＋F(a－1，b，c－1)
＋F(a，b－1，c－1)＋2F(a－1，b－1，c－1)
⑵利用上述递推关系求解下题：
书架上有3本不同的数学书，4本不同的物理书，5本不同的化学书，将它们全部竖起排成一行，如果要求同类的书本身互不相邻，一共有多少种不同的排法？